- •Лабораторная работа № 20 изучение упругих свойств пружины
- •Теоретическая часть
- •Описание установки
- •Экспериментальная часть.
- •Литература
- •Вывод зависимости коэффициента жесткости пружины от ее параметров
- •Определение коэффициента жесткости пружины статическим методом
- •Определение коэффициента жесткости пружины динамическим методом
Лабораторная работа № 20 изучение упругих свойств пружины
Цель работы:
Изучение упругих свойств пружины, изготовленной из проволоки круглого сечения. Определение коэффициента жесткости пружины из закона Гука и из периода вертикальных колебаний груза на пружине. Расчет модуля сдвига материала проволоки.
Оборудование:
Установка, включающая в себя штатив с закрепленными на нем датчиками силы и перемещения, набор пружин и грузов, электронный блок управления Cobra3, компьютер.
Продолжительность работы– 4 часа.
Теоретическая часть
Рассмотрим
спиральную пружину, один конец которой
закреплен, а к другому концу приложена
сила
![]() ,
направленная вдоль оси пружины
,
направленная вдоль оси пружины![]() .
Если пружина находится в равновесии,
то силы, действующие на любую часть
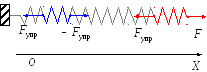
пружины, уравновешены (рис.1), в частности:
.
Если пружина находится в равновесии,
то силы, действующие на любую часть
пружины, уравновешены (рис.1), в частности:![]() .
Силы упругости
.
Силы упругости![]() и
и![]() действуют в каждом поперечном сечении
пружины и являются силами взаимодействия
двух частей пружины, разграниченных
данным сечением. По закону Гука сила
упругости пропорциональна деформации
пружины
действуют в каждом поперечном сечении
пружины и являются силами взаимодействия
двух частей пружины, разграниченных
данным сечением. По закону Гука сила
упругости пропорциональна деформации
пружины![]() :
:
![]() ,
(1)
,
(1)
где
![]() - проекция силы упругости на ось
- проекция силы упругости на ось![]() ,
направленную вдоль оси пружины (рис.1),
,
направленную вдоль оси пружины (рис.1),![]() - коэффициент жесткости пружины,
деформация
- коэффициент жесткости пружины,
деформация![]() считается
положительной при растяжении и
отрицательной при сжатии пружины.
считается
положительной при растяжении и
отрицательной при сжатии пружины.
|
|
|
Рис. 1. Силы в растянутой пружине |
Измерив силу
упругости при заданной деформации, при
помощи формулы (1) можно рассчитать
коэффициент жесткости
![]() .
Этот метод определения
.
Этот метод определения![]() называетсястатическим.
называетсястатическим.
Вертикально
подвешенную пружину можно растянуть,
закрепив на ее нижнем конце груз массы
m. В положении равновесия
действующая на груз сила тяжести![]() уравновешена силой упругости
уравновешена силой упругости![]() .
Из условия равновесия груза следует
.
Из условия равновесия груза следует
![]() (2)
(2)
Но, если груз сместить из положения равновесия вдоль вертикальной оси и затем отпустить, то он начнет совершать колебания, которые описываются формулой
![]() ,
,
где
![]() - амплитуда колебаний,
- амплитуда колебаний,![]() -
циклическая частота,
-
циклическая частота,![]() - период колебаний,
- период колебаний,![]() - начальная фаза, зависящая от смещения
груза из положения равновесия и его
скорости в начальный момент времени.
Период колебаний пружинного маятника
не зависит от амплитуды колебаний и
может быть вычислен по формуле
- начальная фаза, зависящая от смещения
груза из положения равновесия и его
скорости в начальный момент времени.
Период колебаний пружинного маятника
не зависит от амплитуды колебаний и
может быть вычислен по формуле
![]() ,
(3)
,
(3)
Измерив период
колебаний груза известной массы, с
помощью формулы (3) можно определить
коэффициент жесткости пружины. Этот
метод определения
![]() называетсядинамическим.
называетсядинамическим.
Одной из упругих характеристик материала является модуль сдвига N. Величина N вводится как коэффициент пропорциональности между касательным напряжением и углом сдвига в законе Гука для деформации сдвига (иллюстрации сказанному приведены в приложении). Растяжение пружины можно рассматривать как совокупность элементарных сдвигов в объеме материала под действием сил упругости.
Зная коэффициент
жесткости
![]() пружины, ее
радиус
пружины, ее
радиус
![]() ,
число витков пружины
,
число витков пружины![]() и радиус проволоки
и радиус проволоки![]() можно рассчитать модуль сдвига материала
проволоки
можно рассчитать модуль сдвига материала
проволоки![]() из которой изготовлена пружина:
из которой изготовлена пружина:
![]()
![]() (4)
(4)
Вывод формулы (4) приведен в Приложении 1.