
1 семестр / Линейная Алгебра / модуль 3 / Кривые и поверхности Анимация
.docxМодуль 3. Кривые и поверхности второго порядка.
Для групп МП_13,14,15,18.
Этот модуль стоит, как и все 14 баллов.
Базовый уровень (без анимации + дополнительные задания) принесет от 2 до 4 баллов. (Это, в оценках, между 3 и 4).
Задания повышенного уровня сложности (принимаются после сдачи базового уровня) принесут оставшиеся 10 баллов и освободят от опроса 3 и индивидуального задания 3.
Сроки сдачи всего 14 и 16 ноября. В эти же дни будет опрос № 3 и работа над индивидуальным заданием № 3.
Отчет по этому модулю нужно оформить в виде, см. папку «lab7». Но вместо pdf файла, вставляем docx файл!
То есть программы оформить в m-файлах.
При составлении текстового отчета, при необходимости, для связности текста можно и нужно вставлять элементы программы и рисунки, получающиеся в результате решения заданий.
Дома читаем Кривелева, приносите его на занятия. Для того чтобы легче было изучать примеры из этого учебника, выложены м-файлы к Главе 5. Программы в примерах излишне для нас наворочены. Редактируйте эти файлы (сохранив копии) по принципу «отбрось все лишнее», оставляя суть, касающуюся аналитической геометрии. Особенно это касается изображений поверхностей второго порядка. Нам нужно видеть сечения поверхностей, чтобы понимать, как они устроены. Учтите, что в своих программах Вы должны понимать каждую строчку! Так что если Вы используете новые приемы Вы должны понимать, как они работают.
В качестве примера, посмотрите м-файл «конус _5_38 изм», насколько в нем упрощена программа 5.38.
Кривые второго порядка
У кого нет с собой Кривелева, читайте папку СРС из модуля 2, ищите необходимые Вам сведенья.
Матлаб обладает рядом встроенных функций для упрощенного построения графиков некоторых функций. Одна из таких функций ezplot.
Пример1.
figure, axis equal, axis([-1 1 -1 1]), grid on, hold on
ezplot('x^2+y^2=1')
Задание 1. Создать 6 графических подобластей.
figure
subplot(3,2,1), axis equal, axis([-1 1 -1 1]), grid on, hold on
subplot(3,2,2), axis equal, axis([-1 1 -1 1]), grid on, hold on
итд subplot(3,2,3), subplot(3,2,4), subplot(3,2,5), subplot(3,2,6),
В первой построить эллипс, a>b, отметить фокусы, директрисы, изобразить описывающий его прямоугольник,
во второй области построить эллипс, в котором b>a, тоже все отметить,
далее гиперболу, сопряженную гиперболу, у гипербол построить асимптоты,
параболу.
В шестой подобласти изобразить на одном графике эллипс, a>b, обе гиперболы, асимптоты.
Пусть a=4, b=3. А для второй подобласти a=3, b=4.
Поверхности второго порядка
Изучить все по Кривелеву и м-файлам из главы 5. Творчески переработать (в сторону упрощения)
Задание 1. Провести исследование поверхностей второго порядка методом сечений.
Однополосного гиперболоида, двуполостного гиперболоида, гиперболического параболоида, эллиптического параболоида.
Например, по однополосному параболоиду я должна увидеть примерно такое исследование:
разбиваем графическое окно на несколько подобластей
в первом рисуем все, что касается сечений параллельных плоскости УОХ,
во втором ... ZOX,
в третьей ZOY,
в четвертой, пятой и шестой изображаем саму поверхность в различных ракурсах, регулируемых view(), пересекаемые плоскостями z=+- 0, 5, x=+-0,5,y=+-0, 5.
Гиперболический параболоид обязательно пересечь плоскостью z=0, и увидеть, что остается в положительном направлении OZ и отрицательном.
Задание 2. Задан эллиптический параболоид.
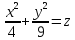 .
.
Его пересекает плоскость z=4. Построить эти фигуры в пространстве и убедиться, что они действительно пересекаются. Аналитически составить уравнение кривой пересечения эллиптического параболоида и плоскости. Изобразить кривую пересечения графически, убедиться, что аналитическое решение подтверждает графическое (иными словами, построенная кривая является сечением эллиптического параболоида заданной плоскостью)
Анимация.
Изучаем m-файлы из папки «анимация».
1. Вращается прямая, вокруг пересекающейся с ней действительной осью, осью конуса.
2. Однополосный гиперболоид.
Прямая вращается вокруг оси, скрещивающейся с ней, то есть вокруг мнимой оси однополосного гиперболоида. Эта программа демонстрирует линейчатость однополостного параболоида, и показывает, что через каждую точку однополостного гиперболоида проходят две различные прямые, целиком расположенные на этой поверхности.



Кстати двуполостный гиперболоид тоже нашел себе применение:
Свойство двуполостного гиперболоида вращения отражать лучи, направленные в один из фокусов, в другой фокус, используется в телескопах системы Кассегрена и в антеннах Кассегрена.
Применение эллиптического параболоида всем известно!
Часто используется свойство параболоида вращения собирать пучок лучей, параллельный главной оси, в одну точку — фокус, или, наоборот, формировать параллельный пучок излучения от находящегося в фокусе источника. На этом принципе основаны параболические антенны, телескопы-рефлекторы,прожекторы, автомобильные фары и т.д.
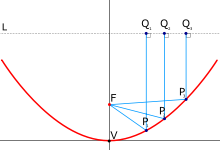
Задание1. Сделать анимацию, вращения прямой вокруг параллельной ей прямой. (Что получится?)
Задание 2. Составить уравнения двух пересекающихся прямых в пространстве, скрещивающихся с осью OZ, их вращением получить однополостный гиперболоид, с осью симметрии OZ.
Задание 3. Составить уравнение прямой в пространстве, пересекающую ось OZ, вращением этой прямой получить конус второго порядка, с осью симметрии OZ.
На опросе помимо теоретического вопроса по теме модуля, будет задание касающиеся устройства мини-программы
t=[-5 5];
M=[0;0;0]; V=[1;1;0];
XYZ=M*ones(size(t))+V*t;
L=plot3(XYZ(1,:),XYZ(2,:),XYZ(3,:),'--r','LineWidth',2);
хотя это касается построения прямой в пространстве, заданной параметрически.
Нужно будет описать каждый элемент: V*t, size(t), ones(size(t)), M*ones(size(t)). И объяснить, что считывает plot3,если аргументы заданы в виде: XYZ(1,:),XYZ(2,:), XYZ(3,:)
Повышенный уровень
*Задание 1*. Аналитически привести уравнение кривой к каноническом виду. Нарисовать график полученной кривой, отметить фокусы, отобразить директрисы.
а)
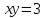
б)
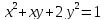
в)
доказать, что уравнение
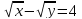 определяет параболу, привести к
каноническом виду, построить кривую,
провести директрису, отметить фокус.
определяет параболу, привести к
каноническом виду, построить кривую,
провести директрису, отметить фокус.
*Задание 2*. Аналитически и графически решить задачу 1.391.
*Задание4*.
Прямая x=y=z+1 вращается вокруг оси oz составить уравнение поверхности вращения.
Самое сложное задание. Доказать, что через каждую точку гиперболического параболоида проходит две пересекающиеся прямые. И сделать анимацию, показывающую, как пространство заполняется пересекающимися прямыми и образует гиперболоид. Для ориентира см. задачу 1.391.
