sss / Задание для МП_11,17,П_12 / учет успеваемости_к_20_02_12 / МП-11_МА / 25_Полунин_лаб1.2
.docx2.Символьное вычисление определённого интеграла.При вычислении определённого интеграла в символьном виде следует задать значения нижнего и верхнего предела в качестве нижнего и верхнего предела в int(f,x,a,b).
Упражнение 2. Вычислить определённые интегралы в символьном виде:
а)
б)
в)
a) >> syms x
>> int(x*cos(x^2),x,0,pi/2)
ans =
1/2*sin(1/4*pi^2)
b) int((1-(x^2))^(1/2),x,-1,1)
ans =
1/2*pi
c) >> int(x*exp(3*x),x,0,1)
ans =
1/9+2/9*exp(3)
3. Интегральные суммы и суммы Дарбу.
Упражнение
3. Создать М-функции, вычисляющие
значения интегральных сумм на отрезке
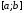с
равномерным разбиениемна
отрезков для точек, взятых на:
а) левом
б) правом конце элемента разбиения;
с*) делящих
их в произвольном заданном отношении
a) function [sum1]=int_niz(f,n,a,b)
sh =(b-a)/n;
sum1=0;
for i=0:n-1
sum1 = sum1 + sh*feval(f,(a+i*sh));
end
b) function [sum1]=int_ver(f,n,a,b)
sh =(b-a)/n;
sum1=0;
for i=1:n-1
sum1 = sum1 + sh*feval(f,(a+i*sh));
end
c) function [sum1]=int_l(f,n,l,a,b)
sh =(b-a)/n;
s = l*sh/(l+1)
sum1=0;
for i=0:n-1
sum1 = sum1 + sh*feval(f,((a+i*sh));
end
Проверка
function [f]=xpl(x)
f=x+1;
а) >> int_niz('xpl',5,0,5)
ans =
15
>> int_niz('xpl',10,0,5)
ans =
16.2500
>> int_niz('xpl',100,0,5)
ans =
17.3750
>> int_niz('xpl',1000,0,5)
ans =
17.4875
б) >> int_ver('xpl',5,0,5)
ans =
14
>> int_ver('xpl',10,0,5)
ans =
15.7500
>> int_ver('xpl',100,0,5)
ans =
17.3250
>> int_ver('xpl',1000,0,5)
ans =
17.4825
в) >> int_l('xpl',5,1,0,5)
ans =
17.5000