sss / Задание для МП_11,17,П_12 / учет успеваемости_к_20_02_12 / МП-11_МА / 06 Коноплёв Алексей Андреевич

№1

Упражнение 3. Создать М-функции, вычисляющие значения интегральных сумм на отрезке с равномерным разбиениемна отрезков для точек, взятых на:

б) правом конце элемента разбиения;

с*) делящих их в произвольном заданном отношении

Проверить работу М-функции для функции на отрезке при разбиении его на два равных элемента, пункт с) – деление отрезка пополам.

б) function [sum]=intsump(f,a,b,n)

% Интегральная сумма справа

% intsump(f,a,b,n)

% f - функция, зависящая от x;

% a - начальное, b - конечное значение;

% n - разбиение;

sum=0;

for i=1:n

sum=sum+(feval(f,(a+(b*((i)/n)))))*((i/n)-((i-1)/n));

end;

end

с) function [sum]=intsuml(f,a,b,n,l)

% Интегральная сумма взятая в отношении l

% intsum(f,a,b,n)

% f - функция, зависящая от x;

% a - начальное, b - конечное значение;

% n - разбиение;

% l - отношение;

sum=0;

for i=1:n

sum=sum+(feval(f,(a+(b*((i-(1/l))/n)))))*((i/n)-((i-1)/n));

end;

end

Проверка:

а)

(функция: function [sum]=intsum(f,a,b,n)

% Интегральная сумма слева

% intsum(f,a,b,n)

% f - функция, зависящая от x;

% a - начальное, b - конечное значение;

% n - разбиение;

sum=0;

for i=1:n

sum=sum+(feval(f,(a+(b*((i-1)/n)))))*((i/n)-((i-1)/n));

end;

end)

intsum(f,1,2,2)

ans=1.5000

б)intsump(f,1,2,2)

ans=2.5000

с) intsuml(f,1,2,2,2)

ans=2

№2

Упражнение 4. Создать М-функции, вычисляющие значения верхних и нижних сумм Дарбу на отрезке с равномерным разбиением на отрезков. Проверить работу М-функции для функции на отрезке при разбиении его на два равных элемента.

а)Верхняя сумма дарбу:

function [sum]=sumdarp(f,a,b,n)

sum=0;

g=@(x)(-1)*(feval(f,x));

for i=1:n

[m,fval]=fminbnd(g,(a+b*((i-1)/n)),(a+b*(i/n)),optimset('TolX',1e-12,'Display','off'));

sum=sum+fval*((i/n)-((i-1)/n));

end

end

б)Нижняя сумма дарбу:

function [sum]=sumdar(f,a,b,n)

sum=0;

for i=1:n

[m,fval]=fminbnd(f,(a+b*((i-1)/n)),(a+b*(i/n)),optimset('TolX',1e-12,'Display','off'));

sum=sum+fval*((i/n)-((i-1)/n));

end

end

Проверка:

а) sumdar(f,1,2,2)

ans=1.5000

б) sumdarp(f,1,2,2)

ans=-2.5000

№3

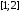_{Упражнение 5.} Вычислить интегральные суммы и суммы Дарбу для на отрезке при

_{а) intsum(f,1,2,1000)}

_{ans = 0.0699}

_{б) intsump(f,1,2,1000)}

_{ans = 0.0695}

_{в) sumdar(f,1,2,1000)}

_{ans =0.0695}

_{г) sumdarp(f,1,2,1000)}

_{ans =-0.0699}

_№4

Упражнение 6. Вычислить Сравнить с результатами упражнении 5, вычислив разности между численным значением интеграла и интегральными суммами и суммами Дарбу.