sss / Задание для МП_11,17,П_12 / учет успеваемости_к_20_02_12 / МП-11_МА / 22_Ильичев_Прак_1
.docxПрактикум 1
Упражнени 1
а) >> syms x
>> f=int(x*sin(5*x),x)
f =
1/25*sin(5*x)-1/5*x*cos(5*x)
Результат в матлабе сошелся с результатом в тетради
б) >> f=int(1/((x^2+1)*(x-2)^2),x)
f =
2/25*log(x^2+1)+3/25*atan(x)-1/5/(x-2)-4/25*log(x-2)
Результат в матлабе сошелся с результатом в тетради.
в)
>>
syms x
>> int(1/(sqrt(x^2+1)),x)
ans =
asinh(x)
>> syms a
>> int(1/(sqrt(x^2+a^2)),x)
ans =
log(x + (a^2 + x^2)^(1/2))
>> f=int(1/sqrt(x^2+2*x+3),x) (Matlab 2008a)
f =
asinh(1/2*2^(1/2)*(x+1))
>> f=int(1/sqrt(x^2+2*x+3),x) (Matlab 2010b)
f =
log(x + (x^2 + 2*x + 3)^(1/2) + 1)
Результаты в матлабе сошлись с результатами в тетради.
(Пояснение, почему я два раза проинтегрировал одно и тоже: разные версии Матлаба дают разные ответы, как вы можете это увидеть)
Упражнение 2
Вычислить определённые интегралы в символьном виде:
а) >> f=int(x*cos(x^2),x,0,pi/2)
f =
sin(pi^2/4)/2
б) >> f=int(sqrt(1-x^2),x,-1,1)
f =
pi/2
в) >> f=int(x*exp(3*x),x,0,1)
f =
(2*exp(3))/9 + 1/9
Упражнение 3
Создать
М-функции, вычисляющие
значения интегральных сумм на отрезке
с
равномерным разбиениемна
отрезков для точек, взятых на:
а) Левом
function S = fofo( f,a,b,n )
syms x
S=0;
k=(b-a)/n;
for y=a:k:b-k
g=subs(f,x,y);
S=S+g*k;
end
end
Функция f=x+1
f=x+1
a=0
b=5
Результат при n=5
>> fofo(f,a,b,n)
ans =
15
Результат при n=10
>> fofo(f,a,b,n)
ans =
16.2500
Результат при n=100
>> fofo(f,a,b,n)
ans =
17.3750
Результат при n=1000
>> fofo(f,a,b,n)
ans =
17.4875
Результат вычисленный мной в тетради: 17,5. Результаты сошлись.
Функция f=x2
f=x^2
a=0
b=1
Результат при n=5
ans =
0.2400
Результат при n=10 ans =
0.2850
Результат при n=100
ans =
0.3284
Результат при n=1000
ans =
0.3328
Результат вычисленный мной в тетради: 0,(3). Результаты сошлись.
б) Правом конце разбиния:
function S = fofo( f,a,b,n )
syms x
S=0;
k=(b-a)/n;
for y=a+k-k/100000000:k:b
g=subs(f,x,y);
S=S+g*k;
end
end
При n=5
ans =
20.0000
При n=10
ans =
18.7500
При n=100
ans =
17.6250
При n=1000
ans =
17.5125
с) делящих
их в произвольном заданном отношении
function S = fofi( f,a,b,n,g )
syms x
S=0;
k=(b-a)/n;
for y=a+k/g:k:b
g=subs(f,x,y);
S=S+g*k;
end
end
>> n=5;
>> g=12;
>> fofi(f,a,b,n,g)
ans =
15.4167
Упражнение 4
Создать
М-функцию, вычисляющую значение нижней
суммы Дарбу на отрезке
с равномерным разбиением на
отрезков.
function S = fofa( f,a,b,n )
syms x
S=0;
k=(b-a)/n;
for y=a:k:b-k
ymin=fminbnd('x+1',y,y+k);
g=subs(f,x,ymin);
S=S+g*k;
end
end
Результат при n=5
ans =
15.0003
Результат при n=10
ans =
16.2503
Результат при n=100
ans =
17.3753
Результат при n=1000
ans =
17.4878
Результат в тетради: 17,5. Результат в Матлабе сошелся с результатом в тетради.
Упражнение
4. Создать М-функции, вычисляющие
значения верхних и нижних сумм Дарбу
на отрезке
с равномерным разбиением на
отрезков. Проверить работу М-функции
для функции
на отрезке
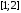при разбиении его на два равных элемента.
Нижние суммы Дарбу
function S = fofa( f,a,b,n )
syms x
S=0;
k=(b-a)/n;
for y=a:k:b-k
ymin=fminbnd('x+0',y,y+k);
g=subs(f,x,ymin);
S=S+g*k;
end
end
>> fofa(f,a,b,n)
ans =
1.2501
Верхние суммы Дарбу
function S = fofa( f,a,b,n )
syms x
S=0;
k=(b-a)/n;
for y=a:k:b-k
ymax=fminbnd('-x+0',y,y+k);
g=subs(f,x,ymax);
S=S+g*k;
end
end
>> fofa(f,a,b,n)
ans =
ans =
1.7499
Упражнение 5
Упражнение
5. Вычислить интегральные суммы
и суммы Дарбу для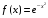
на отрезке
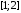при
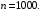
Интегральная сумма на левом конце разбиения:
>> syms x
>> f=exp((-x)^2);
>> a=1;
>> b=2;
>> n=1000;
>> fofo(f,a,b,n)
ans =
15.0159
Интегральная сумма на правом конце разбиения:
ans =
15.0159
Нижняя сумма Дарбу:
ans =
14.9669
Верхняя сумма Дарбу:
ans =
15.0130
Упражнение 6
Упражнение
6. Вычислить
Сравнить с результатами упражнении 5,
вычислив разности между численным
значением интеграла и интегральными
суммами и суммами Дарбу.
>> quad('exp(-(x.^2))',1,2)
ans =
0.1353
Разница между численным значением и интегральной суммой на левом конце разбиения:
0.1353-15.0159