Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МИЭТ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

первый курс / BDZ_linal_matan

.pdf

Скачиваний:

Добавлен:

05.06.2015

Размер:

739.2 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 139 10 11 12 13 > Следующая >>>

16)

а)

y = ln(0,5sin5x) ;

y =

+ 2

ö4

б)

ø .

17)

а)

y = cosarctg ex ;

y =

2 - x3

б)

(1+ x2 )3

y = -

+ ln tg x ;

18)

а)

2sin2 x

4x3

y =

(1- x)4 .

б)

19)а) y = (x2 -1)(1+ x )(2 - 32x );

б) y = 1+ arccos2x .

y =

öæ

4x +

3 ÷ç

20) а)

øè

;

б)

y = ln arcsin 5x .

21) а)

y = ln(x +1+

x2 + 2x) ;

y =

2 - x + 2x

б)

+ x)2

5tg

+ 4

y = arctg

22) а)

;

y =

б)

2 + x

23) а)

y = ln arccos3x ;

y =

1- 5x + 2x4

б)

(2 + x)

y = arcsin

24) а)

1- x2 ;

y =

öæ

-1÷ç

+1÷

б)

x -1

øè

ø .

PDF created with pdfFactory Pro trial version www.pdffactory.com

25)а)

б)

26)а)

б)

27)а)

б)

28)а)

б)

29)а)

б)

30)а)

б)

y =

1+ x3

− (x2 −1)(1− x)

3(1− x2 )

;

y = arctg 2 + x

2 − x .

y = arccos

;

x + 3

y =

1− 2x

−

1+ x2

34 2x −1 .

y = arccos e2x ;

x3 −

y =

1+ x2 .

y = lnsin

x + 3

;

y =

x + x3

(3 − x2 )

y = arcsin(cos x) ;

y =

−

e2x

1+ x2

− x2 .

y = 2arctg ln x

;

1− 5

y =

3x2

3 − x2 .

14.2. Найти уравнения касательной и нормали к кривой в заданной точке.

3 − x

1)y = 2x − 3 ,

	y =		2x
		+ x2 ,
2)	1

3)	y =		5 − x2 ,
4)	y = arctg 2x ,
		8

5)y = 4 + x2 ,

6)y = x × e−x ,

x = 2 .

x= 2 .

x=1 .

x = 0 .

x = −1.

PDF created with pdfFactory Pro trial version www.pdffactory.com

	y =		x3 + 2x2
7)	y =		(x -1)2 ,
7)			(x -1)2 ,
	y = (x -1) × 3														,
8)	y = (x -1) × 3										x + 2				,

9)	y =			10 - x2 ,
10)	y = arccos3x ,
11)	y = x5 + 2x2 - 4x - 3 ,

12)	y =				x2 + 5 ,
	y =			1
13)	y =	1		+ x2 ,
13)		1		+ x2 ,
14)	y = 2−x2 sin πx ,
	y = x2 arcsin										x
15)	y = x2 arcsin
15)				2 ,
	y = 3												,
16)	y = 3				1- cos3 2x								,
17)	y = x3 ctg πx ,
18)	y = x × 2−x ,
19)	y = ln x ,
	y = x × 3								,
20)	y = x × 3					1- x			,
21)			1−x2
21)	y = e			,
	y = (x +1) × 3													,
22)	y = (x +1) × 3									3 - x				,

23)	y =				2x3 ,
	y = 3						,
24)	y = 3				x -1		,
	y = arcsin							x -1
25)	y = arcsin											,
25)				2								,
	y =		x2 - 3x + 6
26)	y =					x2						,
26)						x2						,

27)y = (2x +1) × 31- x ,

28)y = 3e−2x2 ,

29)y = 13 - x2 ,

x = −2 .

x = 6 .

x =1 . x = 0 .

x = −2 .

x = 2 .

x= −1.

x= 0 .

x = 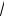3 .

x = 0 .

x=14 .

x= −1.

x=1 .

x= 9 .

x=1 .

x = 2 .

x = 2 . x =1 .

x=1 .

x= 3 .

x= 2 .

x =1 .

x = −2 .

PDF created with pdfFactory Pro trial version www.pdffactory.com

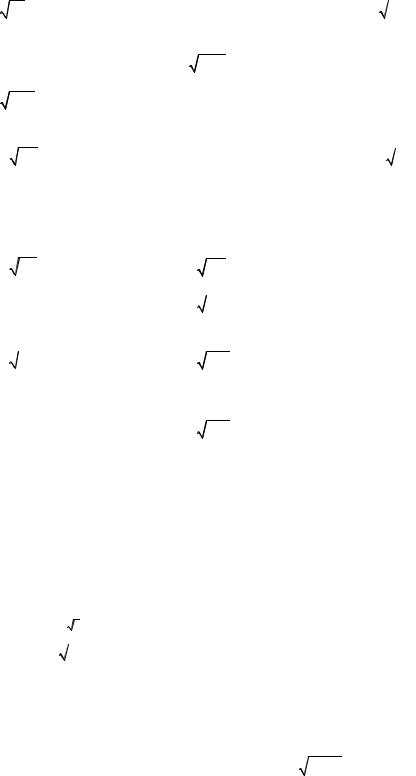
	y = 2arcsin	2x -1	x = 0,5.
30)		2 ,

14.3. Вычислить приближенно с помощью первого дифференциала.

																									1
																												.
1)				1,1				.					2) ln1,2 .											3)		0,9		.
4) sin2 0,1.													5) 3												1
4) sin2 0,1.													5) 3			0,76					.			6) 1,05 .
7) 4										.														9) cos2 0,15 .
7) 4			1,28							.			8) ln0,9 .											9) cos2 0,15 .
		1
	4													e0,2 .											3				.
						0,8
10)						0,8						.	11)											12)			0,9
															1										e−0,1 .
13)	ln1,3 .												14)	1,08 .										15)	e−0,1 .
		1
	5													5						.					sin2 0,15 .
							1,2
16)							1,2				.		17)					0,8						18)
														3					.						e0,15 .
19)	2ln0,94 .												20)	3				1,1	.					21)	e0,15 .
		1
														4									.		cos2 0,2 .
					1,1
22)					1,1				.				23)					1,16						24)
25)	ln0,8 .												26)	arctg0,1.										27)	arccos0,05 .
														4								.			arctg0,05 .
28)	arcsin0,1.												29)	4			1,15					.		30)	arctg0,05 .

14.4. Вычислить пределы с помощью правила Лопиталя.

ex -

- x -1

lim

x→0

cos x

-1

lim

x→0

sin x .

lim

tg x - x

- ln(1+ x) .

x→0 arcsin x

lim

ex2 -1

x→0 cos x -1 .

lim lncos x

x→0

x .

	lim	x - arctg x
2)							.
	x→0			x3
	lim		π - 2arctg x
			æ			1	ö
	x→∞				+
4)			ln ç1			x	÷
			è				ø .
	lim		x2 - 4
6)	x→2 x3 - 8 .
	lim		2x - 3x

8)	x→0 x 1- x2 .
10)	lim lnsin 2x
	x→0		lnsin x .

PDF created with pdfFactory Pro trial version www.pdffactory.com

lim

11)

x→+∞ ex .

lim

ex - e−x

13)

x→0 sin x cos x .

lim

ln(1- cos x)

15)

x→0

ln tg x

lim

lnsin x

ctg x .

17)

x→+0

19)

lim arcsin x - x

x→0

xarcsin x .

lim

ex -1- x

x(ex -1)

21)

x→0

lnç x -

lim

tg x

23)

x→π

lim

−1 x2

25)

x→0

lim

ex - esin x

tg3 x

27)

x→0

lim

4x - 2x

29)

x→0 x

1- x2 .

lim

ln x

12)

x→0 lnsin x .

- 3

lim

14)

x→2

x -

2 .

lim

x + cos x

16)

x→∞ x - cos x .

lim

x - sin x

x - tg x .

18)

x→0

lim

sin2 x - x2

20)

x2 sin2 x .

x→0

lim

x - arctg x

xarctg x .

22)

x→0

lim

ln x - xln x

24)

x→1

ln2 x .

lim

x tg x

26)

x→0 sin2 x .

lim

e1 x -1

28)

1 x .

x→∞

- 3

lim

30)

x→3

x -

3 .

14.5. Найти наибольшее и наименьшее значения функции на отрезке.

	y =	e−x
1)		x + 2 ,		[0; 2].

2)	y = xarctg x ,			[–1; 2].
3)	y = ex sin x ,			[0; 2π].
4)	y = x + 1			[0,5; 2].
			x ,
	y =		2x
5)		(x	+1)2 ,	[0; 3].

	y =	x2	- 3x + 2
6)		x2 + 2x +1 ,		[0; 3].

				85

PDF created with pdfFactory Pro trial version www.pdffactory.com

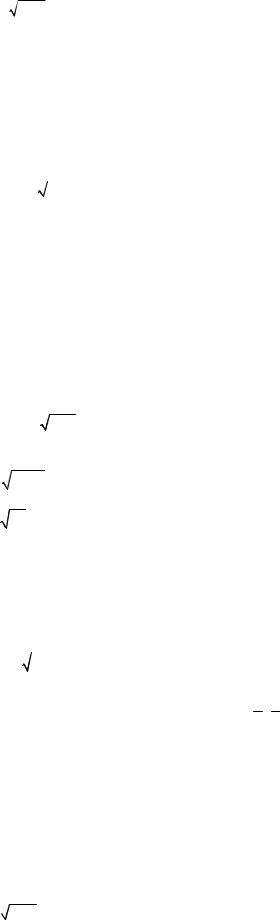
7)y = x 3x -1 ,

y =	x2	+1

		x ,
8)

9)y = x2ex ,

	y =			2x - 2
10)	y =	x2 - 2x + 2										,
	y = (x +1) 3										,
11)	y = (x +1) 3							x			,
	y =		sin x
										,
12)		2 + cos x								,
13)	y = sin x + cos2 x ,
	y = arcsin							2x
	y = arcsin
14)							1+ x2 ,
	y =	x2		- 4x + 5
15)	y =			x		- 2						,
15)				x		- 2						,
	y = (x + 2) 3												,
16)	y = (x + 2) 3								x +1				,
	y =	arcsin x
17)	y =
17)			1- x2 ,
	y = 3				e−x ,
18)	y = 3		x2		e−x ,
19)	y = x2 e−2x ,
20)	y = xln x ,
21)	y = x − arctg x ,

22)	y = x3 ×						x2 -1 ,
23)	y = sin4 x + cos4 x ,
24)	y = cos x + 1 cos2x
24)						2						,
25)	y = cos2x +								1 cos4x
25)								2				,

y = arctg x - 1 ln (1+ x2 )

26)2 ,

27)y = x +1 ×ln(x +1) ,

[0; 1].

[0,01; 100]. [–3; 1].

[–1; 4]. [–1; 3].

[0; 2π]. [0; π].

[–1; 2].

[2,5; 5]. [–2; 1].

[–0,5; 0,5]. [–2; 1]. [0; 3]. [0,3; 3]. [0; 1].

[1; 3].

éê- π ; π ùú ë 4 4 û .

[0; 2π].

[0; π].

[0; 2]. [–1; 10].

PDF created with pdfFactory Pro trial version www.pdffactory.com

28)	y = arctg x - 12 ln (1+ x2 ),			[0; 4].
29)	y = arctg1		- x	[0; 1].
	1		+ x ,
	y =		×ln(x - 2) ,
30)		x - 2		[3; 12].

14.6. Исследовать функцию и построить график.

План исследования: а) область определения; б) четность, нечетность, периодичность; в) точки пересечения с осями координат; г) поведение на бесконечности; д) асимптоты (вертикальные, наклонные); е) первая производная, критические точки; ж) вторая производная, точки перегиба; з) таблица; и) график.

y =

x2 -1

x - 2

y =

4) y = xln2 x .

x +1

y = x + arcctg 2x .

y =

ln(x -1)

x -1 .

y =

x2 +1

8) y = xln (x

+1).

x .

y =

2 - ln x

- x .

10)

x .

y = (x −1)ln(x −1) .12)

y =

e−x

11)

2 + x

13)

y = xln x .

14)

y =

1+ ln x

x .

ex−2

y = -

+ 3 x

y =

15)

16)

x -1 .

y = x − 2arctg x .

y = ln

+1.

17)

18)

x + 2

y = (x2 -1)e−x .

y = x - 3

+1.

19)

20)

y =

e−x

y = ln

21)

+1 .

22)

-1 .

y = e

y =

3 (x +1)2 − x

23)

x−1

24)

PDF created with pdfFactory Pro trial version www.pdffactory.com


	y =	1− x2			y = 2x + arctg x .
25)	y =	x2 .		26)
25)		x2 .		26)
27)	y = x × e−x .			28)	y = x − ln x .
	y =	e−x			y = (1− x)ln(1− x) .
29)	y =	2x + 4	.	30)	y = (1− x)ln(1− x) .

14.7.Решить задачу экономического характера.

1)Зависимость спроса от цены одного вида продукции задается равенством

x = p2 +100 , где х – количество проданных единиц (спрос); р – цена единицы продукции. Определить максимальный доход.

2) Себестоимость производства x изделий в неделю определяется формулой

C(x) = 600 +100x −100ln x (руб.), x ³1 . Определить минимум средней себестоимости одного изделия. Каково количество изделий, при котором он достигается?

3)Компания по продаже музыкальных дисков организует продажу диска популярной группы в городе с 50 тыс. потенциальных

покупателей. Маркетинговыми исследованиями установлено, что после t дней телевизионной рекламы диск купят (1- e−αt )100% покупателей. Стоимость телевизионной рекламы C(t) = 40000 + 30000t (руб.). Сколько дней нужно проводить телевизионную рекламу, чтобы получить максимальную прибыль от продажи, если известно, что стоимость одного диска 200 руб. и α = 0,03 ?

4)Себестоимость продукции определяется функцией C(x) = 9000 + 30x , доход

R(x) = 300x − x2

30. При каких значениях спроса х прибыль возрастает?

5)Гостиничный комплекс сдает в среднем за сутки 500 номеров по цене 750 руб. за номер. Изучение спроса показало, что увеличение стоимости проживания на 10 руб. ведет к уменьшению сдаваемых номеров на 5. Считая, что уравнение зависимости спрос-цена линейно, определить цену за номер так, чтобы доход гостиницы был максимален.

6)Компания планирует производство и продажу новых электрических приборов. После маркетинговых исследований установлено, что недельный спрос составляет 200 приборов по цене 600 руб. за штуку и 300 по цене 400 руб. Недельная фиксированная (не зависящая от количества выпускаемых приборов) себестоимость выпуска одного прибора – 150 руб. Найти объем недельного

PDF created with pdfFactory Pro trial version www.pdffactory.com

производства с максимальной прибылью, считая, что уравнение зависимости спрос-цена линейное.

7) Себестоимость производства x транзисторов (в неделю) определяется уравнением

C(x) = 5000 + 2x (руб.). Доход от продажи x транзисторов составляет

	R(x) =10x −	x2
	R(x) =10x −	1000 (руб.). Определить максимальную прибыль.
		1000 (руб.). Определить максимальную прибыль.

8)Исследования агронома показали, что если в саду посажено 30 вишневых деревьев, то каждое из них дает в среднем по 20 кг ягод в сезон. Если на той же площади высадить дополнительные деревья, то урожай с каждой вишни уменьшается на 0,5 кг на каждое дополнительное дерево. Сколько деревьев следует посадить в саду для наибольшего урожая? Найти максимальный урожай.

9)Фирма сдает в аренду автомобили: ежедневно 200 машин по 900 руб. в день за аренду одного автомобиля. Если тариф поднять на 50 руб., спрос на аренду упадет на 20 машин в день. По какому тарифу выгодно предлагать в аренду автомобили? Какова ежедневная выручка фирмы?

10)Исследование рынка продажи аквариумов в крупном городе показало, что цена аквариума может быть задана функцией p = 900 − 30ln x , где x – число продаваемых аквариумов в неделю. Определить максимальную прибыль от продажи аквариумов, если в торговую сеть они поступают по цене 400 руб.

11)Косметическая компания планирует выпуск новой линии губной помады. Маркетинговые исследования показали, что в большом городе зависимость спроса

− x

от цены будет p =10e 2 , где р – цена; х – число (в сотнях) продаваемых тюбиков губной помады в неделю. Найти максимальный доход компании.

12) Стоимость производства сноубордов определяется функцией C(x) =10000 + 80x , где

− x

х – количество сноубордов в неделю. Зависимость цены и спроса p =15000e 10 . Найти максимальный доход недельной продажи сноубордов.

13) Зависимость спроса от цены одного вида продукции задается равенством

x = 5000 − p2 , где х – количество проданных единиц (спрос); р – цена единицы продукции. Определить максимальный доход.

14) Себестоимость производства x изделий в неделю определяется формулой

C(x) =10 + 20x − 20ln x (руб.), x ³1 . Определить минимум средней себестоимости одного изделия. Каково количество изделий, при котором он достигается?

PDF created with pdfFactory Pro trial version www.pdffactory.com

15)Отель для туристов сдает в среднем за сутки 200 номеров по цене 900 руб. за номер. Изучение спроса показало, что увеличение стоимости проживания на 20 руб. ведет к уменьшению сдаваемых номеров на шесть. Считая, что уравнение зависимости спрос-цена линейно, определить цену за номер так, чтобы доход гостиницы был максимален.

16)Себестоимость продукции определяется функцией C(x) = 700 + 40x , доход

R(x) =100x − x2

5. При каких значениях спроса х прибыль возрастает?

17)Компания планирует производство и продажу новой марки телефона. Маркетинговые исследования показали, что недельный спрос составляет 200 телефонов по цене 6000 руб. за один телефон и 300 по цене 5000 руб. Недельная фиксированная (не зависящая от количества выпускаемых изделий) себестоимость выпуска одного телефона – 1500 руб. Считая, что уравнение зависимости спрос- цена линейное, найти объем недельного производства с максимальной прибылью.

18)Себестоимость производства x аккумуляторов (в неделю) определяется уравнением

C(x) = 2500 +1,5x (руб.). Доход от продажи составляет R(x) = 5x −	x2
	500 (руб.). Найти
максимальную прибыль.

19)Исследования агронома показали, что если в саду посажено 40 грушевых деревьев, то каждое из них дает по 35 кг фруктов в сезон. Если на той же площади высадить дополнительные деревья, то урожай с каждой груши уменьшается на 0,5 кг на каждое дополнительное дерево. Сколько деревьев следует посадить в саду для наибольшего урожая? Найти максимальный урожай.

20)Фирма сдает в аренду автомобили: ежедневно 150 машин по 800 руб. в день за аренду одного автомобиля. Если тариф поднять на 40 руб., спрос на аренду упадет на 20 машин в день. По какому тарифу выгодно предлагать в аренду автомобили? Какова ежедневная выручка фирмы?

21)Исследование рынка продажи принтеров определенной модели в крупном городе показало, что цена принтера может быть задана функцией p =1800 − 40ln x , где x – число продаваемых принтеров в неделю. Определить максимальную прибыль от продажи принтеров, если в торговую сеть они поступают по цене 1100 руб.

22)Зависимость спроса от цены одного вида продукции задается равенством

x = p3 + 200 , где х – количество проданных единиц (спрос); р – цена единицы продукции. Определить максимальный доход.

PDF created with pdfFactory Pro trial version www.pdffactory.com

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 139 10 11 12 13 > Следующая >>>

Соседние файлы в папке первый курс

#
05.06.20151.13 Mб560358595_61DBE_otvety_na_bilety_po_istorii_rossii.doc
#
05.06.2015739.2 Кб44BDZ_linal_matan.pdf
#
05.06.2015125.68 Кб22ekonomika_41-52.docx
#
05.06.20151.83 Mб29ekonomika_53-60.docx
#
05.06.201584.07 Кб32ekz_istor.docx
#
05.06.2015273.92 Кб28Filosofia_otvety_ekzamen.doc
#
05.06.2015432.64 Кб18istoria_bilety.doc