
LARIONOV
.pdf8.Объясните основные выводы, следующие из опытов Никурадзе.
9.Основные формулы для определения коэффициента гидравлического трения при турбулентном режиме течения.
10.Причины потери энергии при изменении размеров потока.
11.Потери напора при расширении потока. Что называется диффузором?
12.Потери напора при сужении потока. Что называется конфузором?
13.Основные формулы для определения потерь энергии при изменении направления потока.
14.Определение понятия фильтрация.
15.Определение основных понятий процесса фильтрации.
16.Два варианта определения скорости движения жидкости сквозь фильтрующий материал.
17.Закон Дарси для определения фильтрационного расхода.
18.Анализ движения безнапорных вод к колодцу.
19.Анализ притока безнапорных вод к водосборной траншее.
20.Фильтрация сквозь сетчатые фильтры.
21.Основные понятия безнапорного движения жидкости.
22.Определение гидравлически наивыгоднейшего профиля.
PDF created with pdfFactory Pro trial version www.pdffactory.com
2.Тепловые процессы
винженерной практике природообустройства
Под тепловыми понимаются самопроизвольные необратимые процессы распространения теплоты в пространстве. При этом под процессом распространения теплоты понимается обмен внутренней энергией между отдельными областями рассматриваемой среды, происходящий только при наличии разности температур, поскольку в соответствии со вторым законом термодинамики самопроизвольный перенос теплоты происходит от тела с более с высокой температурой к телу с более низкой температурой. При
отсутствии разности температур процесс переноса теплоты прекращается и наступает тепловое равновесие тел.
Наука, изучающая указанные выше процессы, называется теплопередачей. Различают основные три способа распространения теплоты в природе: теплопроводность, тепловое излучение и конвекция.
Под теплопроводностью понимается молекулярный перенос теплоты в телах или между ними, обусловленный разностью температур в рассматриваемом пространстве. Для реализации теплообмена необходимо непосредственное соприкосновение тел или частиц тела с различной температурой. При этом интенсивность движения частиц с меньшей внутренней кинетической энергией возрастает, а с большей внутренней кинетической энергией уменьшается, т.е. происходит обмен энергией их теплового движения.
Теплопроводность обусловлена движением микрочастиц вещества: в газах перенос энергии осуществляется в результате диффузии, в жидкостях и твердых телах-диэлектриках с помощью упругих волн, в металлах в основном в результате диффузии свободных электронов.
Процесс распространения теплоты с помощью электромагнитных волн и обусловленный только температурой и оптическими свойствами излучающего тела представляет тепловое излучение. Процесс превращения внутренней энергии вещества в энергию излучения, перенос излучения и его поглощения веществом называется теплообменом излучением.
Под конвекцией теплоты, которая возможна только в движущейся среде, понимается процесс переноса
теплоты при перемещении объемов жидкости или газа в пространстве из области с одной температурой в область с другой. При этом перенос теплоты неразрывно связан с переносом самой среды. Конвекция теплоты всегда связана с теплопроводностью, и совместный процесс переноса теплоты конвекцией и теплопроводностью называют конвективным теплообменом.
Винженерной практике часто определяют конвективный теплообмен между потоками жидкости или газа и поверхностью твердого тела - данный процесс конвективного теплообмена называют конвективной теплоотдачей или просто теплоотдачей.
Всистемах теплоснабжения часто происходит процесс теплообмена между различными жидкостями или жидкостью и газом через разделяющую их твердую стенку. Процесс передачи теплоты от горячей жидкости (газа) к холодной через разделяющую их твердую стенку называется теплопередачей.
2.1.Процесс теплообмена теплопроводностью
2.1.1.Температурное поле и температурный градиент
Вобщем случае процесс теплообмена теплопроводностью в твердом теле сопровождается изменением температуры как в пространстве, так и во времени. В обобщенном виде пространственно-временное
изменение температуры записывается уравнением
PDF created with pdfFactory Pro trial version www.pdffactory.com
t = f (x, y, z,τ) , |
(2.1) |
которое определяет совокупность значений температуры во всех точках пространства в данный момент времени и является математическим выражением температурного поля.
Если значения температуры изменяются не только при изменении координат пространства, но и во времени, то такое температурное поле называется нестационарным (неустановившимся).
При неизменных значениях температуры в точках пространства во времени тепловой режим является установившимся. Такое температурное поле называется стационарным:
t = f (x, y, z); |
∂t |
= 0. |
(2.2) |
|
∂τ |
||||
|
|
|
Температурное поле называется одномерным при изменении только температуры только по одной координате:
t = f (x, τ); |
∂t |
= |
∂t |
= 0 . |
(2.3) |
|
∂y |
∂z |
|||||
|
|
|
|
Наиболее простым для анализа является одномерное стационарное температурное поле:
t = f (x); ∂∂τt = 0; ∂∂yt = ∂∂zt = 0.
Соединив в температурном поле условной поверхностью все точки, имеющие одинаковую температуру, получим поверхность равных температур - изотермическую поверхность. Изотермические поверхности обладают тем же свойством, что и поверхность равного давления: в пространстве они не пересекаются.
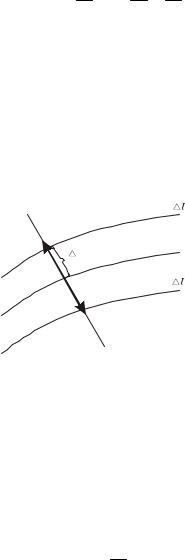
При пересечении семейства изотермических поверхностей плоскостью получим линии равных температур - изотермы (рис.2.1).
h |
|
t+ |
gradt |
|
|
|
t |
|
|
n |
|
|
|
|
|
|
t - |
|
|
q |
Рис.2.1. Изотермы и температурный градиент
Очевидно, что температура в теле изменяется только при переходе от одной изотермы к другой, при этом наибольший перепад температуры на единицу длины приходится на направле-ние нормали к изотермической поверхности. Положительное изменение температуры по направлению нормали к изотермической поверхности называется температурным градиентом, представляющим собой вектор, нормальный к изотермической поверхности, направленный в сторону возрастания температуры и
определяемый выражением
r ∂t |
|
|
grad t = n0 ∂n |
, |
(2.4) |
PDF created with pdfFactory Pro trial version www.pdffactory.com

где n0 - единичный вектор, нормальный к изотермической поверхности и направленный в сторону
∂t
возрастания температуры; ∂n - производная от температуры по нормали n. Легко заметить, что скалярная
величина температурного градиента различна для различных точек изотермической поверхности: она больше там, где меньше расстояние n между изотермическими поверхностями.
2.1.2. Тепловой поток
При изучении процессов теплопроводности в твердых телах установлено, что количество теплоты,
проходящее через элементарную площадку изотермической поверхности за бесконечно малый промежуток времени, пропорционален температурному градиенту, площади поверхности элементарной площадки и промежутку времени:
|
|
dQ = −λ |
∂t |
dFdτ , |
(2.5) |
||
|
|
|
|||||
|
|
τ |
|
∂n |
|
||
|
|
|
|
|
|||
где dQτ - элементарное количество теплоты, Дж; |
dF - площадь элементарной площадки изотермической |
||||||
поверхности, м2; |
∂t |
- температурный градиент, |
К/м; dτ - бесконечно малый промежуток времени, с; λ - |
||||
∂n |
|||||||
|
|
|
|
|
|
||
коэффициент пропорциональности, Вт/мК.
Выражение (2.5) называется законом Фурье. Опытным путем установлено, что коэффициент пропорциональности λ в законе Фурье является физическим (теплофизическим) параметром вещества, характеризующим способность вещества проводить тепловую энергию, и называется коэффициентом теплопроводности.
Коэффициент теплопроводности представляет собой количество теплоты, которое проходит в единицу
времени через единицу площади изотермической поверхности при температурном градиенте равном единице. Чем больше значение λ, тем большей теплопроводностью обладает вещество. В общем случае теплопроводность данного вещества не является величиной постоянной: для твердых тел коэффициент λ зависит от температуры, а для жидких и газовых сред - еще и от давления.
Количество теплоты dФ, прошедшее в единицу времени через изотермическую площадку dF,
называется тепловым потоком:
dФ = |
dQτ |
= −λ |
∂t |
dF . |
(2.6) |
dτ |
|
||||
|
|
∂n |
|
||
Величина теплового потока, проходящего через единицу площади изотермической поверхности, называется
плотностью теплового потока:
q = ddFФ = dFddQττ [Вт/м2].
Плотность теплового потока является векторной величиной:
r |
|
∂t |
|
|
q = −n0 |
λ |
|
. |
(2.7) |
∂n |
||||
Вектор плотности теплового потока, так же как и вектор температурного градиента, направлен по нормали к изотермической поверхности, а поскольку теплота всегда передается от более горячих частей
PDF created with pdfFactory Pro trial version www.pdffactory.com

∂t
тела к более холодным, то векторы ∂n и q лежат на одной прямой, но направлены в противоположные
стороны.
Скалярная величина вектора плотности теплового потока равна:
q = −λ |
∂t |
. |
(2.8) |
|
|||
|
∂n |
|
|
Полное количество теплоты, прошедшее за время τ через изотермическую поверхность F, равно:
Qτ = −òτ |
òλ |
∂t |
dFdτ [Дж]. |
(2.9) |
|
||||
0 |
F |
∂n |
|
|
Таким образом, для определения количества теплоты, проходящего через какую-либо поверхность твердого тела посредством теплопроводности, необходимо знать температурное поле внутри рассматриваемого тела, что и является основной задачей при исследовании процесса теплопроводности и решении инженерных задач.
2.1.3. Дифференциальное уравнение теплопроводности
При выводе дифференциального уравнения теплопроводности приняты следующие допущения: тело, в котором происходит процесс теплопроводности, будем считать однородным, изотропным с постоянными физическими характеристиками, деформация рассматриваемого объема, обусловленная изменением температуры, бесконечно мала по сравнению с величиной самого объема.
Для вывода уравнения будем опираться на закон сохранения энергии, согласно которому количество теплоты dQ1 , введенное в элементарный объем твердого тела извне за время dτ посредством
теплопроводности, а также количество теплоты, выделенное внутренними источниками теплоты тела dQ2 ,
должно равняться изменению внутренней энергии тела dU :
dQ1 + dQ2 = dU . |
(2.10) |
Для определения составляющих последнего выражения в произвольной системе декартовых координат
выделим в теле элементарный параллелепипед со сторонами dx, |
dy, dz (рис.2.2). |
Z |
dz |
dQx |
dQ |
|
x |
dx dy
O dQy dQz
X
Y
Рис.2.2. К выводу дифференциального уравнения теплопроводности
PDF created with pdfFactory Pro trial version www.pdffactory.com

Количество теплоты, которое подводится к граням элементарного объема за время dt в направлении координатных осей, равно dQx , dQy , dQz . Через противоположные грани параллелепипеда за тот же
промежуток времени будет отводиться количество теплоты dQx′, dQ′y , dQz′ .
Вначале рассмотрим процесс в проекции на ось ОХ. Количество теплоты, подводимое к элементарному объему через грань dy, dz за время dt, равно:
dQx = qxdydzdt,
где qx - проекция плотности теплового потока на ось ОХ.
Количество теплоты, отводимое от элементарного объема в направлении оси ОХ, равно: dQx′ = q′x dydzdτ .
Разница этих величин представляет собой количество теплоты, остающееся в элементарном объеме:
dQ |
= dQ - dQ¢ = (q |
x |
- q¢ )dydzdτ . |
(2.11) |
|
1x |
x |
x |
x |
|
|
По аналогии с выводом дифференциального уравнения равновесия жидкости можно записать, что
q¢x = qx + ∂¶qxx dx .
Тогда
dQ |
= - |
∂qx |
dxdydzdτ . |
(2.12) |
|
||||
1x |
|
¶x |
|
|
|
|
|
||
По аналогии для двух других координатных осей
dQ1y = - ¶¶qyy dxdydzdτ, dQ1z = - ¶¶qzz dxdydzdτ . (2.13)
Окончательно имеем, что количество теплоты, подведенное к элементарному объему теплопроводностью, равно:
|
æ |
¶q |
|
¶qy |
|
¶q |
ö |
dQ1 |
= dQ1x + dQ1y + dQ1z = -ç |
|
x + |
|
+ |
|
z ÷dxdydzdτ . (2.14) |
|
¶y |
|
|||||
|
è |
¶x |
|
¶z ø |
|||
Будем называть мощностью внутренних источников теплоты qν |
то количество теплоты, которое |
||||
выделяется внутренними источниками в единицу времени в единице объема тела: |
|||||
dQ2 = qνdvdτ, |
(2.15) |
||||
где dv = dxdydz - объем элементарного параллелепипеда. |
|
||||
Изменение внутренней энергии элементарного параллелепипеда |
объемом dv определяется из |
||||
следующего выражения: |
|
|
|
||
dU = cρdv |
¶t |
dτ = cρ |
¶t |
dxdydzdτ, |
(2.16) |
|
|
||||
|
¶τ |
¶τ |
|
||
где c - теплоемкость, Дж/(кг×К); r - плотность вещества элементарного параллелепипеда.
Подставив значения составляющих уравнения (2.10) из (2.14), (2.15), (2.16) и проводя соответствующие
сокращения, получим |
|
|
|
|
|
|
|
|
|
|
cρ |
¶t |
æ |
¶q |
|
¶qy |
|
¶q |
ö |
+ qν . |
|
|
= -ç |
|
x + |
|
+ |
|
z ÷ |
(2.17) |
||
¶τ |
|
¶y |
|
|||||||
|
è |
¶x |
|
¶z ø |
|
|
||||
PDF created with pdfFactory Pro trial version www.pdffactory.com
|
Проекции плотности |
теплового |
|
|
|
потока |
|
|
на |
|
|
соответствующую |
|
координатную ось равны: |
|||||||||||||||||||||||||||
qx |
= -λ |
¶t |
, qy = -λ |
|
¶t |
, qz |
= -λ |
¶t |
|
. С учетом этого выражение (2.17) примет вид |
|||||||||||||||||||||||||||||||
|
|
¶y |
¶z |
||||||||||||||||||||||||||||||||||||||
|
|
¶x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶t |
|
|
æ |
|
2 |
t |
|
|
|
|
¶ |
2 |
t |
|
|
¶ |
2 |
t |
ö |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
cρ |
|
|
|
= λç |
|
¶ |
+ |
|
|
|
+ |
|
÷ + qν . |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
¶τ |
|
|
|
2 |
|
¶y |
2 |
¶z |
2 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è ¶x |
|
|
|
|
|
|
|
|
ø |
|
|
|
||||||||||||||
|
Разделив в последнем выражении левую и правую часть на cρ , окончательно получим |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
¶t |
æ |
|
|
2 |
t |
|
|
¶ |
2 |
t |
|
|
¶ |
2 |
t |
ö |
|
qν |
|
|
|
qν |
|
|
|||||||||
|
|
|
|
|
|
|
|
= a ç |
|
¶ |
|
+ |
|
|
+ |
|
|
÷ + |
= aÑ2t + |
, |
(2.18) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
¶τ |
|
|
|
2 |
|
¶y |
2 |
|
¶z |
2 |
cρ |
cρ |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
è ¶x |
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
||||||||||||||||
где коэффициент a = |
|
λ |
|
называется коэффициентом температуропроводности, м2/с. |
|||||||||||||||||||||||||||||||||||||
cρ |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Данный коэффициент является теплофизическим параметром вещества, характеризующим скорость изменения температуры в теле. Значение коэффициента зависит от природы вещества. Если коэффициент теплопроводности характеризует способность тела (вещества) вообще проводить теплоту, то коэффициент температуропроводности является мерилом теплоинерционных свойств вещества. Другими словами, скорость изменения температуры в любой точке тела будет тем больше, чем больше значение коэффициента а. Если в теле отсутствуют внутренние источники теплоты, то выражение (2.18) принимает вид уравнения Фурье:
¶t |
= aÑ2t . |
(2.19) |
|
¶τ |
|||
|
|
При наличии внутренних источников теплоты, но в условиях стационарного теплового поля, выражение (2.19) принимает вид уравнения Пуассона:
æ |
2 |
t |
|
2 |
t |
|
2 |
t |
ö |
|
qν |
|
|
ç |
¶ |
+ |
¶ |
+ |
¶ |
÷ |
+ |
= 0 . |
(2.20) |
||||
¶x |
2 |
¶y |
2 |
¶z |
2 |
λ |
|||||||
è |
|
|
|
|
|
ø |
|
|
|
При отсутствии внутренних источников теплоты и в условиях стационарного теплового поля выражение (2.19) принимает вид уравнения Лапласа:
¶2t |
+ |
¶2t |
+ |
¶2t |
= 0 . |
(2.21) |
|
¶x2 |
¶y2 |
¶z2 |
|||||
|
|
|
|
Таким образом, уравнения (2.18) - (2.21) устанавливают связь между временным и пространственным изменением температуры при различных условиях протекания процесса теплопроводности.
Дифференциальное уравнение теплопроводности в самом общем виде описывает бесконечное множество явлений теплопроводности. Чтобы из этого бесконечного множества явлений выделить конкретно рассматриваемый (единичный) процесс и дать его математическое описание, необходимо к
дифференциальному уравнению теплопроводности присоединить математическое описание всех частных особенностей конкретного анализируемого процесса. Такие частные особенности, которые совместно с
дифференциальным уравнением дают возможность полного математического описания конкретного процесса теплопроводности, называются краевыми условиями, или условиями однозначности.
2.1.4. Краевые условия, или условия однозначности
Выделение частного процесса теплопроводности из всей совокупности процессов осуществляется заданием следующих условий однозначности.
PDF created with pdfFactory Pro trial version www.pdffactory.com
1.Начальные условия, которые определяют распределение температуры в теле в начальный момент времени процесса и в основном используются при нестационарном процессе теплопроводности.
2.Физические условия, определяемые теплофизическими параметрами тела, в котором происходит теплообмен теплопроводностью.
3.Геометрические условия, которые определяют форму и размеры тела.
4.Граничные условия, которые характеризуют взаимодействие рассматриваемого тела с окружающей
средой.
Граничные условия задаются несколькими способами.
Граничные условия первого рода - при этом задается распределение температуры на поверхности тела для каждого момента времени:
tc = f (x, y, z, τ), |
(2.22) |
где tc - температура на поверхности тела; x, y, z, - координаты поверхности тела.
В частном случае, когда температура на поверхности тела постоянна в течение всего процесса теплопроводности, уравнение (2.22) принимает упрощенный вид tc = const.
Неизвестным остается плотность теплового потока.
Граничные условия второго рода - в данном случае задается значение плотности теплового потока
каждой точки поверхности тела (поверхностная плотность теплового потока) и любого момента времени:
qп = f (x, y, x, τ) . |
(2.23) |
В частном случае плотность теплового потока остается постоянной по поверхности тела и во времени: qп = q0 = const.
Неизвестной остается температура на поверхности тела.
Граничные условия третьего рода - в данном случае задаются температура среды tср , окружающей
тело, и закон теплообмена между поверхностью тела и окружающей средой, а температура на поверхности тела определяется через температуру окружающей среды.
Для описания процесса теплообмена между окружающей средой и поверхностью тела в данном случае можно использовать закон Ньютона - Рихмана, согласно которому количество теплоты, отдаваемое с единицы поверхности тела в единицу времени, пропорционально разности температур поверхности тела и окружающей среды:
q = α(tc - tcр ), |
(2.24) |
где α - коэффициент пропорциональности, называемый коэффициентом теплоотдачи, Вт/(м2×К).
Коэффициент теплоотдачи является характеристикой интенсивности теплообмена между поверхностью тела и окружающей средой. Численно он равен количеству теплоты, отдаваемому или принимаемому
единицей поверхности тела в единицу времени при разности температур между поверхностью тела и окружающей средой в один градус.
Сопоставляя уравнение Фурье и уравнение закона Ньютона - Рихмана, имеем
æ |
¶t ö |
= α(tср - tc ) . |
|
-λс ç |
|
÷ |
|
|
|||
è |
¶n øc |
|
|
Индекс «с» указывает на то, что температура и температурный градиент относится к поверхности тела.
Тогда окончательно граничные условия третьего рода можно записать в виде
PDF created with pdfFactory Pro trial version www.pdffactory.com
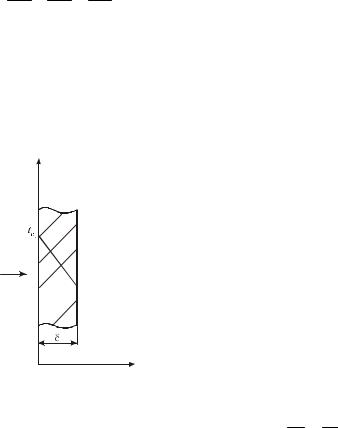
æ |
¶t ö |
= - |
λ |
c |
(tс |
- tср ) . |
(2.25) |
|
ç |
|
÷ |
|
|||||
|
|
|
||||||
è |
¶n øc |
|
α |
|
|
|||
С учетом приведенных условий однозначности рассмотрим наиболее типовые случаи процесса теплопроводности, которые позволяют решать ряд инженерных задач.
2.1.5. Теплопроводность в однослойной плоской стенке
Рассмотрим однородную, изотропную однослойную стенку неограниченной длины и ширины с толщиной, имеющей ограниченный размер, равный δ . При этом считаем, что внутренние источники теплоты в стенке отсутствуют, тепловое поле является стационарным. Материал стенки обладает постоянным коэффициентом теплопроводности.
Для данного случая уравнение теплопроводности имеет вид
¶2t + ¶2t + ¶2t = 0 . ¶x2 ¶y2 ¶z2
При граничных условиях первого рода на наружных поверхностях стенки поддерживается постоянная температура tc1 и tc2 , причем tc1 > tc2 . При обозначенных условиях задачи температура будет меняться
только по толщине стенки в направлении, перпендикулярном плоскости стенки. Если это направление совместить с осью ОХ (рис.2.3),
Z
q
 tc2
tc2
O X
Рис.2.3. Однородная плоская стенка
то температура в направлении двух других координатных осей меняться не будет, т.е. ¶¶yt = ¶¶zt = 0 .
После этих замечаний дифференциальное уравнение теплопроводности примет вид
d 2t |
= 0 . |
(2.26) |
|
dx2 |
|||
|
|
Сформулированные граничные условия первого рода применительно к рассматриваемой задаче записываются следующим образом:
x = 0 t = tc , |
|
|
1 |
(2.27) |
|
x = δ t = tc2 . |
||
|
Легко заметить, что уравнение (2.26) и условия однозначности (2.27) дают полную математическую формулировку задачи, в результате решения которой должно быть найдено распределение температуры в
PDF created with pdfFactory Pro trial version www.pdffactory.com
стенке (температурное поле) и определено количество теплоты, проходящее через плоскую стенку в единицы времени.
Распределение температуры по толщине стенки определяется двойным интегрированием уравнения (2.26). После первого интегрирования имеем
dt |
= grad t = C . |
(2.28) |
|
||
dx |
1 |
|
|
|
Таким образом, температурный градиент по толщине стенки является величиной постоянной.
После второго интегрирования получаем
t = C1 x + C2 . |
(2.29) |
Из последнего выражения видно, что при постоянном коэффициенте теплопроводности температура по толщине стенки меняется по линейному закону.
Из граничных условий (2.27) легко находятся постоянные интегрирования:
C = − |
tc |
− tc |
2 |
; C |
|
= t |
|
. |
1 |
|
2 |
c |
|||||
|
|
|
||||||
1 |
|
δ |
|
|
|
|
||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
Подставив значения постоянных интегрирования в (2.29), определим закон распределения температуры по толщине стенки:
t = tc − |
tc |
− tc |
2 |
x . |
(2.30) |
1 |
|
||||
|
δ |
|
|||
1 |
|
|
|
|
|
|
|
|
|
|
Совместное решение уравнения Фурье (2.8) и выражения (2.28) позволяет определить плотность
теплового потока |
|
|
|
|
|
|
q = |
λ |
(tc |
− tc |
|
). |
(2.31) |
|
δ |
1 |
|
2 |
|
|
Отношение l/d [Вт/(м2×К)] называется тепловой проводимостью стенки, а обратная величина d/l -
тепловым или термическим сопротивлением стенки.
Знание плотности теплового потока позволяет легко определить общее количество теплоты,
передаваемое через поверхность стенки площадью F за время t:
Q = qFτ = |
λ |
(tc |
− tc |
|
)Fτ . |
(2.32) |
||
|
|
δ |
|
1 |
|
2 |
|
|
Преобразовав выражение (2.31) в вид |
tc1 − tc2 |
= |
q |
и подставив |
его в уравнение (2.30), можно |
|||
δ |
|
|
λ |
|||||
|
|
|
|
|
|
|
||
заметить интересную закономерность: при всех прочих равных условиях температура в стенке убывает тем быстрее, чем больше плотность теплового потока.
2.1.6. Теплопроводность в многослойной плоской стенке
Пусть имеем плоскую стенку, состоящую из n плотно прилегающих друг к другу однородных слоев (рис.2.4). Толщина каждого слоя равна δ1, δ2...δn , а коэффициенты теплопроводности каждого
слоя равны соответственно. Граничные условия, как и для однослойной плоской стенки,
задаются граничными условиями первого рода.
Для данных условий необходимо рассмотреть процесс теплопроводности, определить величину теплового потока и температуры на границах раздела между слоями.
PDF created with pdfFactory Pro trial version www.pdffactory.com
