
DZ0
.docxМИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Национальный исследовательский университет «МИЭТ»
Кафедра: Электротехника
Дисциплина: Электротехника, электроника и схемотехника. Электротехника
210100.62 (выпускающая кафедра ИЭМС)
Пояснительная записка
к домашней работе (ДЗ № 0 вариант № 8 )
на тему:
Линейные электрические цепи постоянного тока.
Руководитель: проф.Волков Ю.И.
Выполнил: ст.гр.ЭКТ-24 Емельянов Анатолий
Дата: 22.10.2013
Москва 2013
Задача 1
ϕ1 ϕ2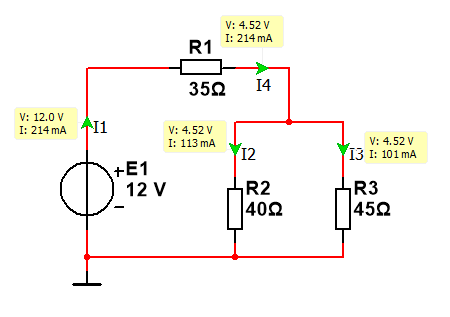
Дано:
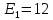 В
В 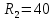 Ом
Ом
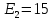 В
В 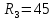 Ом
Ом
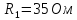
Вычислить:
-
Токи всех ветвей и потенциалы узлов, используя закон Ома, законы Кирхгофа и формулы делителя тока и делителя напряжения.
-
Баланс мощностей (мощность источников, мощность приёмников).
Решение
Найдем токи ветвей:
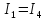
Определим количество уравнений по 1-му закону Кирхгофа:

По 1-му закону Кирхгофа:
Для
1-го узла
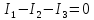
Определим количество уравнений по 2-му закону Кирхгофа:
 =2
=2
Произвольно выберем положительные направления обхода контуров для составления уравнений по второму закону Кирхгофа
I II ϕ1 ϕ2


По 2-му закону Кирхгофа:
Для
1-го контура
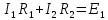
Для
2-го контура
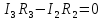
Находим совместное решение системы уравнений
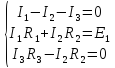
Составляем матрицу:

Решаем её методом Гаусса и получаем неизвестные токи ветвей:




Найдем потенциалы всех узлов:
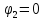
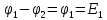 =12
В
=12
В
Баланс мощности
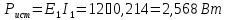
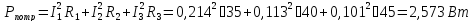
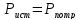
Ответ:
 ,
,
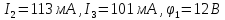 ,
,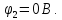
ϕ1 ϕ2
Задача 2

Дано:
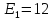 В
В 
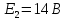


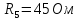
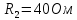
Вычислить:
-
Токи всех ветвей и потенциалы узлов, используя закон Ома, законы Кирхгофа и формулы делителя тока и делителя напряжения.
-
Баланс мощностей (мощность источников, мощность приёмников).
Решение
Найдем токи ветвей:
Определим количество уравнений по 1-му закону Кирхгофа:
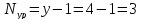
По 1-му закону Кирхгофа:
Для
1-го узла

Для
2-го узла
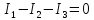
Для
3-го узла
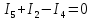
Определим количество уравнений по 2-му закону Кирхгофа:
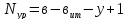 =3
=3
Произвольно выберем положительные направления обхода контуров для составления уравнений по второму закону Кирхгофа
ϕ0 ϕ1 ϕ2 ϕ3 I II III


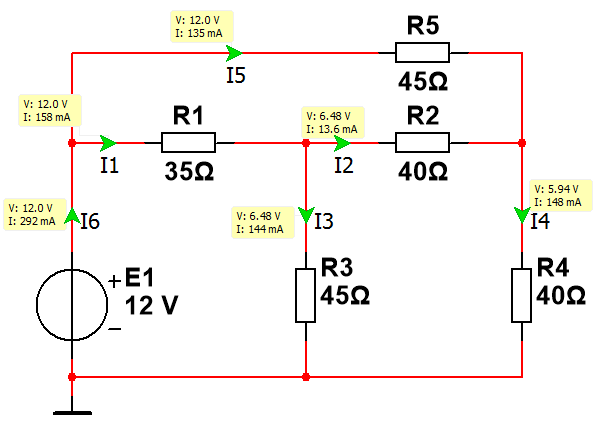
По 2-му закону Кирхгофа:
Для
1-го контура

Для
2-го контура
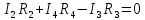
Для
3-го контура

Находим совместное решение системы уравнений

Составляем матрицу:
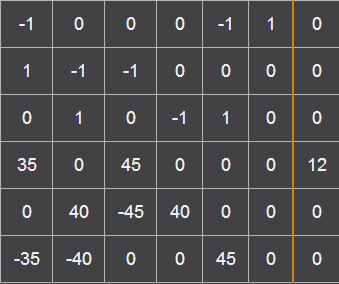
Решаем её методом Гаусса и получаем неизвестные токи ветвей:
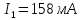
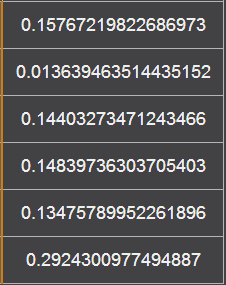
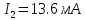
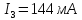

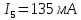
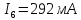
Найдем потенциалы всех узлов:

 =12
В
=12
В
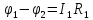
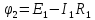 =6.47
В
=6.47
В

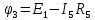 =5.925
В
=5.925
В
Баланс мощности
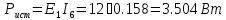
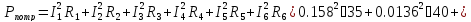

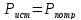
Ответ:
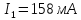 ,
,
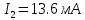 ,
,
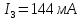 ,
,
 ,
,
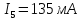 ,
,
 ,
,
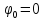 ,
, ,
, =5.925
В
=5.925
В
ϕ0 ϕ1 ϕ2 ϕ3
Задача 3
ϕ2 ϕ4 ϕ3 ϕ1
Дано:
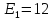 В
В 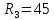 Ом
Ом
 В
В  Ом
Ом
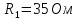
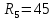 Ом
Ом
 Ом
Ом 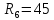 Ом
Ом
Вычислить:
-
Токи всех ветвей и потенциалы узлов, используя закон Ома, законы Кирхгофа и формулы делителя тока и делителя напряжения.
-
Баланс мощностей (мощность источников, мощность приёмников).
Решение
Найдем токи ветвей:
Определим количество уравнений по 1-му закону Кирхгофа:

По 1-му закону Кирхгофа:
Для
1-го узла
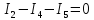
Для
2-го узла
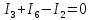
Для
3-го узла
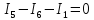
Определим количество уравнений по 2-му закону Кирхгофа:
 =3
=3
Произвольно выберем положительные направления обхода контуров для составления уравнений по второму закону Кирхгофа
ϕ1 ϕ4 ϕ2 ϕ3 II III I


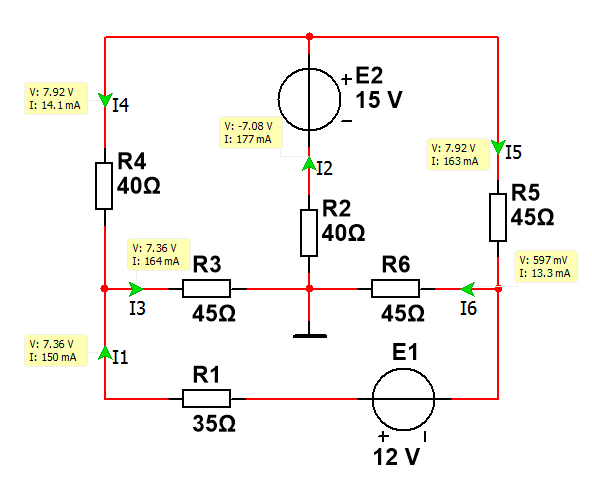
По 2-му закону Кирхгофа:
Для
1-го контура

Для
2-го контура

Для
3-го контура
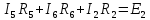
Находим совместное решение системы уравнений
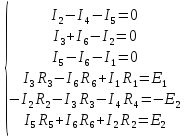
Составляем матрицу:
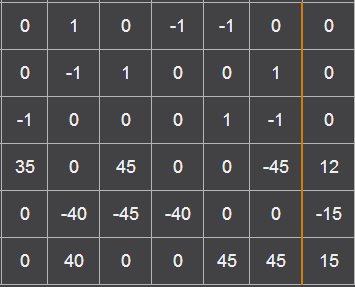
Решаем её методом Гаусса и получаем неизвестные токи ветвей:
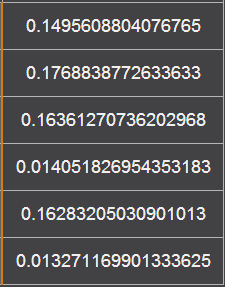
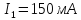


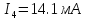

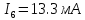
Найдем потенциалы всех узлов:
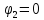
 =
7.38 В
=
7.38 В
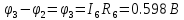
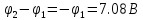
Баланс мощности
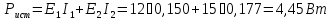
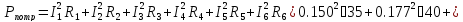
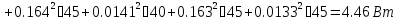
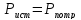
Ответ:
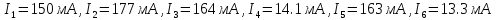 ,
,
 ,
,
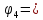 7.38
В
7.38
В

Задача 4

Дано:
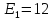 В
В  Ом
Ом
 В
В  Ом
Ом
Вычислить:
-
Токи всех ветвей и потенциалы узлов, используя метод наложения и метод двух узлов.
-
Баланс мощности (мощность источников, мощность приёмников).
Решение
Рассчитаем неизвестные токи ветвей методом наложения
Расчет
схемы с одним источником
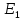 :
:
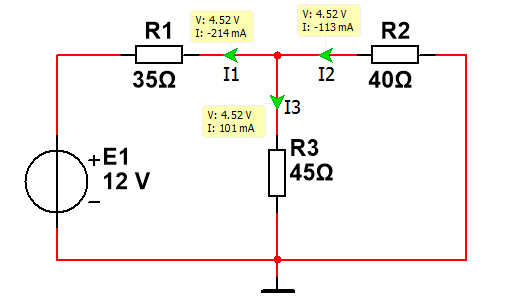
 -0.214
А
-0.214
А
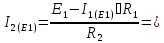 -0.113 А
-0.113 А
 0.101
А
0.101
А
Расчет схемы с
одним источником
 :
:
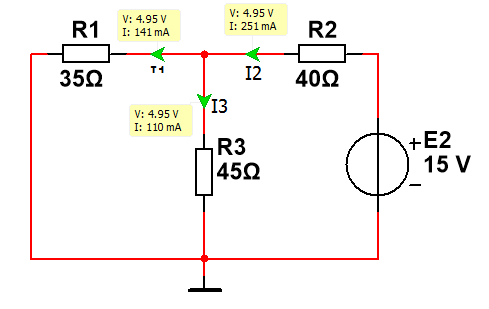
 0.251 А
0.251 А
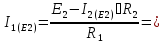 0.141
А
0.141
А
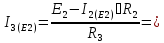 0.110
А
0.110
А
Расчет неизвестных токов:
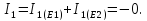 073
А
073
А
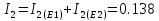 А
А
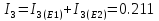 А
А
Рассчитаем неизвестные токи ветвей методом двух узлов:
ϕ1 ϕ2 U12

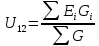 =
=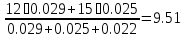

 =
-0.07 А
=
-0.07 А
 А
А
 А
А
Баланс мощности


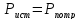
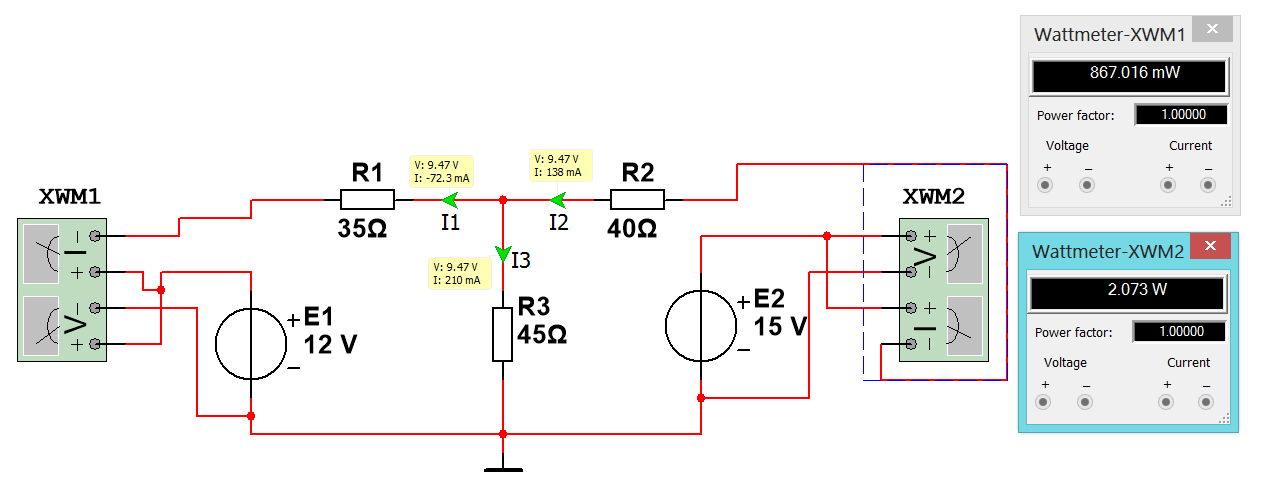
Задача 5
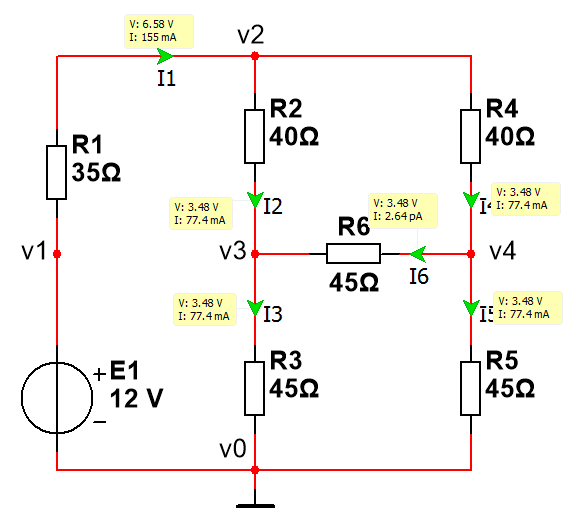
Дано:
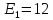 В
В  Ом
Ом

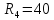 Ом
Ом
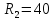 Ом
Ом 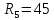 Ом
Ом
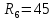 Ом
Ом
Вычислить:
-
Токи всех ветвей и потенциалы узлов, используя закон Ома, законы Кирхгофа, определить ветвь с наибольшей мощностью.
-
Баланс мощности (мощность источников, мощность приёмников).
-
Произвести свёртку электрической цепи относительно выбранной ветви. Составить электрическую цепь, состоящую из источника напряжения или тока, эквивалентного внутреннего сопротивления этого источника и резистора нагрузки в выбранной ветви.
Решение
Найдем токи ветвей:
Определим количество уравнений по 1-му закону Кирхгофа:

По 1-му закону Кирхгофа:
Для
1-го узла
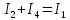
Для
2-го узла

Для
3-го узла
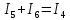
Определим количество уравнений по 2-му закону Кирхгофа:
 =3
=3
Произвольно выберем положительные направления обхода контуров для составления уравнений по второму закону Кирхгофа
I II III



По 2-му закону Кирхгофа:
Для
1-го контура
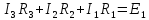
Для
2-го контура

Для
3-го контура
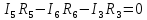
Находим совместное решение системы уравнений
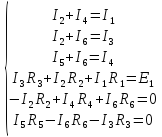
Составляем матрицу:

Решаем её методом Гаусса и получаем неизвестные токи ветвей:
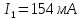

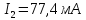
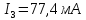
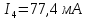

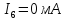
Найдем потенциалы всех узлов:
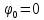
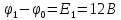

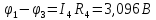
Баланс мощности
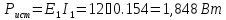

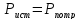
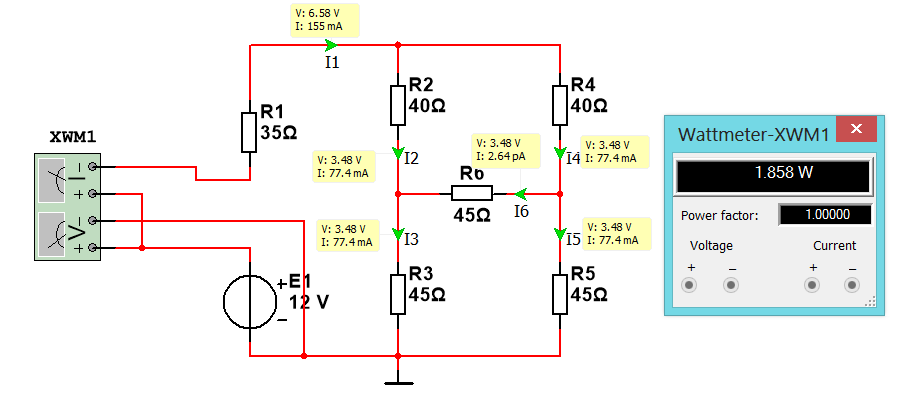
Произведем свёртку электрической цепи относительно выбранной ветви:


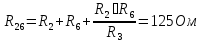
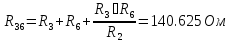
Посчитаем эквивалентое сопротивление:

Проверка:
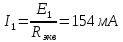
Составим электрическую схему, состоящую из источника напряжения, эквивалентного внутреннего сопротивления этого источника и резистора нагрузки в выбранной ветви:

Ответ:
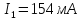
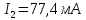

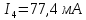


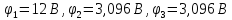 ,
,
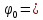 0
В
0
В
