
3. Логические операции
Над переменными логического класса можно совершать логические операции, приведенные в таблице 2.
|
Таблица 2. Логические операции. | ||
|
Символ операции |
Реализующая функция |
Описание |
|
& |
and(x,y) |
Логическое умножение скаляров (результат истина, только если xиyистинны). Логическое покомпонентное умножение массивов одинаковой размерности. Логическое умножение массива на скаляр. |
|
| |
or(x,y) |
Логическое сложение скаляров (результат ложь, только если xиyложны). Логическое покомпонентное сложение массивов одинаковой размерности. Логическое сложение массива со скаляром. |
|
~ |
not(x) |
Логическое отрицание скаляра или всех элементов массива |
|
|
xor(x,y) |
Сложение по модулю 2 скаляров (результат ложен в двух случаях: если xиyоба ложны илиxиyоба истинны). Покомпонентное сложение по модулю 2 массивов одинаковой размерности. Покомпонентное сложение по модулю 2 массива и скаляра. |
Пример 10.
>> x=logical([0 0 1 1])
x =
0 0 1 1
>> y=logical([0 1 0 1])
y =
0 1 0 1
>> x&y
ans =
0 0 0 1
>> x|y
ans =
0 1 1 1
>> xor(x,y)
ans =
0 1 1 0
>> a=1>=2, b=3<4
>> c=a&b
c =
0
>> d=a|b
d =
1
>> t=[1<2 5>3]
t =
1 1
>> ~t
ans=
0 0
Замечание.Если логические операции применить к числовым переменным, то 0 будет рассматриваться как ложь, а все остальные числа как истина.
Пример 11.
>> A=[2 3 0 1]
>> ~A
ans=
0 0 1 0
Пример 12.
>> z1=28-4i;z2=20+10i;
% выясним, верно ли предположение, что модули обоих чисел меньше 29
>> (abs(z1)<29)&(abs(z2)<29)
ans =
1
% предположение оказалось верным
% выясним, верно ли предположение, что модуль хотя бы одного из чисел больше 32
>> (abs(z1)>32)|(abs(z2)>32)
ans =
0
% предположение оказалось неверным
Упражнение 7.Пусть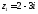 ,
, .
Используя операции отношения и логические
операции, выяснить, какие из приведенных
ниже утверждений верные, а какие нет:
.
Используя операции отношения и логические
операции, выяснить, какие из приведенных
ниже утверждений верные, а какие нет:
1)
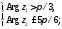 2)
2)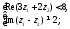 3)
3)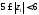 ;
;
4) только одно из чисел
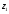 ,
,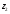 по модулю меньше 4.
по модулю меньше 4.
4. Логическое индексирование
Для того чтобы выделить из исходного массива данные нового массива или изменить группу элементов в исходном массиве, удовлетворяющих заданному условию, целесообразно использовать логическое индексирование. Для выполнения логического индексирования необходимо с помощью логических операций или операций отношения сформировать логический массив, содержащий одинаковое число элементов с исходным массивом. Сформированный логический массив состоит из нулей и единиц, где единичные элементы соответствуют выполнению условия, а нулевые значения – невыполнению этого условия. Если логическое индексирование используется справа от знака присваивания или является одиночной конструкцией, то создается новый массив из тех элементов исходного массива, индексы которых совпадают с индексами истинных элементов логического массива. В том случае если логическое индексирование используется слева от знака присваивания, то элементам исходного массива, индексы которых совпадают с индексами истинных элементов логического массива, присваивается значение, находящееся справа от знака присваивания.
Пример 13.
>> A=[1 2 3 4]
>> L=[1>2 1<2 1<2 1<2]
L =
0 1 1 1
>> B=A(L)
B =
2 3 4
>> A(L)=9
A =
1 9 9 9
Упражнение 8. Сформировать массив
с элементами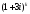 ,
где
,
где .
Используя операцию логического
индексирования, выбрать из массива
числа, удовлетворяющие условиям:
.
Используя операцию логического
индексирования, выбрать из массива
числа, удовлетворяющие условиям:
а)
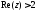 ;
б)
;
б)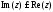 .
.
Упражнение 9. Сформировать массив
с элементами ,
где
,
где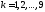 .
Используя операцию логического
индексирования, заменить в этом массиве
числа, удовлетворяющие условию
.
Используя операцию логического
индексирования, заменить в этом массиве
числа, удовлетворяющие условию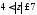 ,
на 0.
,
на 0.
Пример 14.На комплексной плоскости
построить множество точек, координаты
которых удовлетворяют условию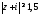 .
.
Программу оформим в виде скрипта, который сохраним под именем Example_2.
В программе используем функцию rand,
которая позволяет генерировать массив
случайных чисел, равномерно распределенных
на отрезке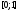 .
Если обратиться к этой функции без
аргумента, то получаем очередное
случайное число. Если у функции задается
один случайный аргумент, то функцияrand(n),
возвращает квадратную матрицуn-го
порядка, элементами которой являются
случайные числа из отрезка [0;1]. Функцияrand(n,m)
возвращает прямоугольную матрицу
размерности
.
Если обратиться к этой функции без
аргумента, то получаем очередное
случайное число. Если у функции задается
один случайный аргумент, то функцияrand(n),
возвращает квадратную матрицуn-го
порядка, элементами которой являются
случайные числа из отрезка [0;1]. Функцияrand(n,m)
возвращает прямоугольную матрицу
размерности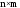 со
случайными числами. Обращениеrand(size(A))
позволяет сгенерировать матицу случайных
чисел, размерность которой совпадает
с размерностью массиваA.
со
случайными числами. Обращениеrand(size(A))
позволяет сгенерировать матицу случайных
чисел, размерность которой совпадает
с размерностью массиваA.
% Построение множества точек, комплексной плоскости, удовлетворяющих
% неравенству
%формируем массив из 100000 случайных чисел, лежащих на [-3;3] оси OX
x=3-6*rand(1,10^5);
%формируем массив из 100000 случайных чисел, лежащих на [-3;3]оси OY
y=3-6*rand(1,10^5);
z=x+y*i;
L=abs(z+i)>=1.5;
plot(x(L),y(L),'.')
grid on
axis equal
axis([-3 3 -3 3])
hold on
line ([-3 3],[0 0],'Color','black')
line ([0 0],[-3 3],'Color','black')
xlabel('Re(z)'),ylabel('Im(z)')
title('|z+i|>=1.5')
Набираем в командной строке команду
>> Example_2
В графическом окне отображается рисунок.
Упражнение 10.На комплексной плоскости построить множество точек, координаты которых удовлетворяют условиям (программы оформить, используя скрипты):
1)
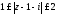 ;
2)
;
2)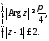
Скрипты
Система MATLABобычно работает в режиме интерпретации команд и операторов: во время работы они выводятся в командной строке, а система выполняет их немедленную обработку и выдает вычисленный результат. Однако в этом режиме нельзя без повторного набора всех операторов повторить предыдущие действия при новых значениях исходных данных; нельзя вернуться и повторить отдельные фрагменты действий или по некоторому условию перейти к другой последовательности операторов. Чтобы избежать этих проблем, часто применяемые последовательности операторов оформляют в виде программ, которые в языкеMATLABназывают М-файлами.
Различают два типа М-файлов: скрипты (script) и функции (function).
Для начала рассмотрим скрипты. Скрипты довольно простой тип М-файлов. Они позволяют автоматизировать выполнение последовательности операторов, которые в ином случае должны были бы многократно вводиться из командной строки. В скрипте можно применять любые команды и функции языка MATLAB. Скрипты не имеют входных и выходных аргументов. Они оперируют данными из рабочей области и могут создавать новые данные для последующей обработки в этом файле. Хотя скрипты не возвращают выходных аргументов, но все переменные сохраняются в рабочей области, так что после выполнения скрипта они могут быть использованы для продолжения вычислений в командном окне.
Создание нового скрипта начинается с
последовательности команд File
 New
New
 Scriptв строке главного
меню. В результате открывается окно
редактора, в котором и набивается
последовательность команд, аналогично
тому, как мы делали это в командном окне.
Строки, набираемые в окне редактора,
автоматически нумеруются. Это позволяет
идентифицировать сообщения об ошибках
набора, выдаваемых в командное окно.
После того, как программа набрана, нужно
ее запомнить. Для запоминания программы,
набранной в окне редактора, нужно
воспользоваться последовательностью
командFile
Scriptв строке главного
меню. В результате открывается окно
редактора, в котором и набивается
последовательность команд, аналогично
тому, как мы делали это в командном окне.
Строки, набираемые в окне редактора,
автоматически нумеруются. Это позволяет
идентифицировать сообщения об ошибках
набора, выдаваемых в командное окно.
После того, как программа набрана, нужно
ее запомнить. Для запоминания программы,
набранной в окне редактора, нужно
воспользоваться последовательностью
командFile
 Save as,
после чего набрать придуманное Вами
имя файла. При этом к имени будет
автоматически добавлено расширение
'.m’. Для того, чтобы
программа была выполнена, нужно в
командном окне набрать имя файла без
расширения. Имена скриптов нельзя
использовать в качестве операндов
арифметических выражений и в качестве
аргументов функций.
Save as,
после чего набрать придуманное Вами
имя файла. При этом к имени будет
автоматически добавлено расширение
'.m’. Для того, чтобы
программа была выполнена, нужно в
командном окне набрать имя файла без
расширения. Имена скриптов нельзя
использовать в качестве операндов
арифметических выражений и в качестве
аргументов функций.
Обратите внимание, что название файла скрипта должно подчинятся тем же правилам, что и названия переменных. Название может содержать только латинские буквы (прописные или строчные) и цифры. Не допускается использовать в названии пробелы или специальные символы (кроме знака подчеркивания). При этом название файла всегда должно начинаться с буквы.
При вызове скрипта MATLABразличает регистр символов в названии файла. Например, для файла с названием “Example_1.m”MATLABбудет выдавать сообщение об ошибке при вызове >>example_1 .
Также обратите внимание, что скрипт должен быть расположен в текущей папке. В противном случае, необходимо сменить текущий каталог на место расположения скрипта, либо указать путь (полный или относительный) к файлу скрипта в строке вызова.
Иногда в процессе отладки scriptа, хочется запустить для проверки отдельный фрагмент программы. Это можно сделать следующим образом: выделить фрагмент, затем дать командуRun(Запуск) в менюDebug(Отладка) или нажать клавишу <F5>. Результат выполнения фрагмента программы появится в командном окне.
