
Лабораторная работа метод Куммера
.docxЛабораторная работа №3.
Тема: Ряды
Для выполнения работы необходимо усвоить теоретический материал:
1. Что называется сумой сходящегося числового ряда?
2. Почему при исследовании сходимости ряда можно отбрасывать любое конечное начальных членов ряда?
3. Предел общего члена ряда равен нулю, можно утверждать, что ряд сходится?
4. Изучите теорему сравнения рядов;
5. В чем суть метода Даламбера сходимости ряда;
6. Какие числовые знакопеременные ряды называются абсолютно сходящимися и, какие условно сходящимися? Приведите примеры;
7. В чем состоит признак Лейбница сходимости рядов?
8. Понятие степенного ряда. Рассмотрите степенные ряды, имеющие нулевой, конечный и бесконечный радиус сходимости;
9. Для каких значений х справедливы разложения в ряд функций:
а) у = ℮х;
б) у = Sinx;
в) ln(1+x)?
Цель работы: Исследование рядов на сходимость. Вычисления суммы ряда
I. Вводные замечания
Рассмотрим
числовой ряд ![]() .
Необходимо установить сходимость ряда,
если ряд сходится, то вычислить сумму
с некоторой точностью .
.
Необходимо установить сходимость ряда,
если ряд сходится, то вычислить сумму
с некоторой точностью .
Исследование
числового ряда целесообразно начинать
с проверки необходимого
условия сходимости
ряда, именно с проверки условия ![]() ,
где аn –
общий член ряда. Если условие не выполнено,
т.е. либо предел
,
где аn –
общий член ряда. Если условие не выполнено,
т.е. либо предел ![]() не
существует, либо он бесконечен, либо
конечен, но равен 0, то ряд
не
существует, либо он бесконечен, либо
конечен, но равен 0, то ряд ![]() расходится.
Если же для ряда
расходится.
Если же для ряда ![]()
![]() ,
то вопрос о сходимости остается открытым,
и требуются дополнительные исследования
на сходимость.
,
то вопрос о сходимости остается открытым,
и требуются дополнительные исследования
на сходимость.
Продемонстрируем это на примерах.
З
а д а
ч а 1. Исследовать
на сходимость ряд ![]() .
.
Р е
ш е н и е. Проверим необходимое
условие, ![]() (этот
придел не существует), а
(этот
придел не существует), а ![]() .
Необходимое условие не выполнено.
Следовательно, данный ряд расходится.
.
Необходимое условие не выполнено.
Следовательно, данный ряд расходится.
Теперь покажем применение основных достаточных признаков сходимости рядов (признак сравнения, признак Даламбера,признак Коши, интегральный признак).
З
а д а
ч а 2. Исследовать
на сходимость ряд ![]() .
.
Р е
ш е н и е. Проверим необходимое условие,
общий член ряда ![]() ,
тогда
,
тогда ![]() следовательно
оно выполнено. Для доказательства
сходимости применим достаточный признак
сравнения рядов. Рассмотрим ряд с общим
членом
следовательно
оно выполнено. Для доказательства
сходимости применим достаточный признак
сравнения рядов. Рассмотрим ряд с общим
членом ![]() и
исследуем его на сходимость: а) Так
как
и
исследуем его на сходимость: а) Так
как ![]() ,
то необходимое условие выполнено.
,
то необходимое условие выполнено.
Для
проверки сходимости ряда ![]() применим
интегральный признак сходимости
рядов. Здесь
применим
интегральный признак сходимости
рядов. Здесь ![]() тогда
тогда ![]() ,
а так как производная
,
а так как производная ![]() для
всех х 2,),
то
для
всех х 2,),
то ![]() убывает
на 2,).
Все условия интегрального признака
выполнены. Тогда
для доказательства нужно вычислить
интеграл
убывает
на 2,).
Все условия интегрального признака
выполнены. Тогда
для доказательства нужно вычислить
интеграл![]() .
Интеграл расходится, но тогда и ряд
.
Интеграл расходится, но тогда и ряд ![]() тоже
расходится. Теперь применим предельный
признак сравнения рядов
тоже
расходится. Теперь применим предельный
признак сравнения рядов 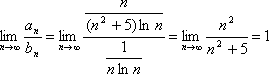 .
Видим, что предел конечен и отличен от
нуля, а так как ряд
.
Видим, что предел конечен и отличен от
нуля, а так как ряд ![]() расходится,
то и ряд
расходится,
то и ряд ![]() будет
расходящимся.
будет
расходящимся.
Достаточные
признаки Коши и Даламбера проиллюстрируем
при исследовании степенных рядов. Ели
проанализировать доказательство
признака Даламбера, то можно заметить,
что для ряда с положительными
членами ![]() существует
предел
существует
предел ![]() .
Если l <
1, то ряд сходится, а при l >
1 общий член ряда не стремится к нулю и,
следовательно, ряд расходится. Аналогичным
образом можно сформулировать признак
Коши.
.
Если l <
1, то ряд сходится, а при l >
1 общий член ряда не стремится к нулю и,
следовательно, ряд расходится. Аналогичным
образом можно сформулировать признак
Коши.
З
а д а
ч а 3.
Найти область сходимости степенного
ряда ![]() .
.
Р е ш е н и е. Применим признак Даламбера к данному ряду:
![]() ; рассмотрим
предел отношения
; рассмотрим
предел отношения
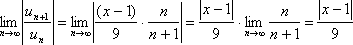 .
.
Тогда
ряд ![]() будет
сходящимся, если будет сходится ряд
будет
сходящимся, если будет сходится ряд 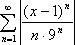 ,
но это возможно, в силу признака Даламбера,
если
,
но это возможно, в силу признака Даламбера,
если![]() т.е.,
если
т.е.,
если ![]() или
-8 < x <
10.
или
-8 < x <
10.
А
при x <
-8 и x >10
ряды 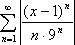 и
и ![]() будут
расходящимися т.к. для всех значений х (-;
-8) (10; )
общий член ряда un не
стремится к нулю.
будут
расходящимися т.к. для всех значений х (-;
-8) (10; )
общий член ряда un не
стремится к нулю.
Напомним,
что из расходимости ряда ![]() ,
вообще говоря, не следует расходимость
ряда
,
вообще говоря, не следует расходимость
ряда ![]() (см.
пример, где
(см.
пример, где ![]() ).
).
Поэтому
необходимо исследовать сходимость
данного ряда на концах интервала сходимости т.е.
при х =
-8 ряд ![]() в
силу признака Лейбница будет сходящимся,
а при х =
10 получим ряд
в
силу признака Лейбница будет сходящимся,
а при х =
10 получим ряд ![]() гармонический,
который расходится. Итак,
областью сходимости степенного
ряда
гармонический,
который расходится. Итак,
областью сходимости степенного
ряда![]() является
промежуток [-8; 10).
является
промежуток [-8; 10).
З
а д а
ч а 4. Найти
область сходимости степенного ряда 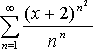 .
.
Р е
ш е н и е. Для исследования ряда применим
признак сходимости Коши к ряду ![]() ,
полагая
,
полагая 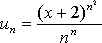 .
Тогда
.
Тогда  ;
;
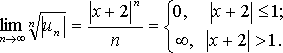
Далее рассуждения аналогичны задачи 3. Получим, что ряд сходится на отрезке [-3; -1]. В этом примере вопрос о сходимости ряда на концах интервала решен без дополнительного исследования.
Теория рядов часто применяется для приближенных вычислений значений функций и определенных интегралов. При этом следует обратить особое внимание на то, как оценить погрешность при замене суммы знакочередующегося ряда его частичной суммой. Если знакочередующийся ряд удовлетворяет условиям теоремы Лейбница, то допускаемая погрешность не превосходит по абсолютной величине первого из отброшенных членов ряда.
З
а д а
ч а 5. Вычислить ![]() с
точностью 0,001.
с
точностью 0,001.
Р е
ш е н и е. Представим ![]() .
.
Теперь воспользуемся разложением
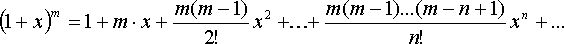 .
.
Положим ![]() получим
получим
![]()
![]()
Получаем
с точностью до 0,001 ![]()
Условия признака Лейбница выполнены и поэтому допускаемая погрешность по абсолютной величине должна быть меньше первого из отброшенных членов:
![]() .
.
Итак, ![]()
Рассмотрим
числовой ряд ![]() для
которого требуется вычислить сумму S с
некоторой точностью .
Заменяя S суммой
конечного числа членов ряда Sn при
этом допускаем погрешность, равную
остаточному члену Rn,
где
для
которого требуется вычислить сумму S с
некоторой точностью .
Заменяя S суммой
конечного числа членов ряда Sn при
этом допускаем погрешность, равную
остаточному члену Rn,
где
Rn = S - Sn .
Для обеспечения заданной точности вычисления необходимо потребовать, чтобы Rn < .
Рассмотрим
сущность метода Куммера. Говорят,
что ряд ![]() (*) сходится
медленно, если для получения его
суммы Sn с
точностью нужно
взять большое число его членов. Но есть
другой ряд сходящийся
быстрее данного ряда (*) т.е. есть два
сходящихся ряда
(*) сходится
медленно, если для получения его
суммы Sn с
точностью нужно
взять большое число его членов. Но есть
другой ряд сходящийся
быстрее данного ряда (*) т.е. есть два
сходящихся ряда ![]() и
и ![]() причем,
причем,
![]() ,
тогда bn = o(an)
при n в
этом случае говорят, что ряд
,
тогда bn = o(an)
при n в
этом случае говорят, что ряд ![]() сходится
быстрее ряда
сходится
быстрее ряда ![]() .
Сущность метода Куммера и заключается
в том, чтобы данный ряд
.
Сущность метода Куммера и заключается
в том, чтобы данный ряд ![]() заменить
рядом сходящимся быстрее, а именно
заменить
рядом сходящимся быстрее, а именно![]() .
.
II. Описание метода
Пусть
ряд ![]() сходится
и сумма его равна S.
Подберем ряд
сходится
и сумма его равна S.
Подберем ряд ![]() сумма
которого известна S1,
причем,
сумма
которого известна S1,
причем, ![]() .
.
Представим
ряд ![]() в
виде
в
виде
 .
.
Так как  т.е.
т.е. ![]() ,
то ряд
,
то ряд  сходится
быстрее ряда
сходится
быстрее ряда ![]() и
поэтому, вычисляя S по
формуле
и
поэтому, вычисляя S по
формуле
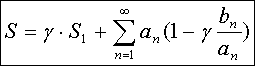 ,
,
получаем требуемую точность при меньшем числе членов.
В
качестве рядов ![]() -
вспомогательных рядов с известными
суммами можно использовать следующие
ряды:
-
вспомогательных рядов с известными
суммами можно использовать следующие
ряды:
|
Ряд |
Сумма |
|
|
|
|
|
|
|
|
|
|
|
ln2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
III. Ход выполнения лабораторной работы
З
а д
а
н и е. Применяя метод Куммера убыстрения
сходимости рядов, вычислить сумму ряда
![]() с точностью .
с точностью .
Выполнение лабораторной работы необходимо разбить на несколько этапов:
1. Если величина, которую нужно вычислять, не представлена числовым рядом, нужно получить это представление (см. Зад. 5).
2. Исследовать ряд на сходимость следуя задачам 1- 4.
3. Определить количество членов ряда n, необходимое для обеспечения заданной точности .
4. Подобрать
вспомогательный ряд ![]() из
таблицы п.II такой,
чтобы
из
таблицы п.II такой,
чтобы ![]() .
.
5. Представить
заданный ряд ![]() в
виде
в
виде  ,
где
,
где ![]() .
.
6. Определить
количество членов ряда  ,
необходимое для обеспечения заданной
точности .
,
необходимое для обеспечения заданной
точности .
7. Вычислить
сумму ряда ![]() с
точностью .
с
точностью .
П р и м е р. Вычислить сумму ряда
![]()
с точностью = 10-6, применяя метод Куммера.
Р е ш е н и е. Сходимость ряда проверить самостоятельно.
Определим количество членов, необходимое для обеспечения требуемой точности = 10-6 .
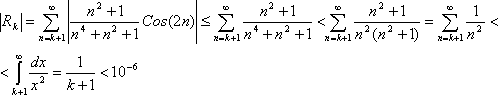
Решая последнее неравенство, получим
k + 1 > 10-6 , k > 10-6 - 1.
Итак, для обеспечения точности = 10-6 необходимо взять примерно106 членов ряда.
Теперь воспользуемся вспомогательным рядом из таблицы
![]() =
= ![]() при
х = 2
при
х = 2
имеем
![]() =
= ![]() .
.
Находим
![]()
Отсюда
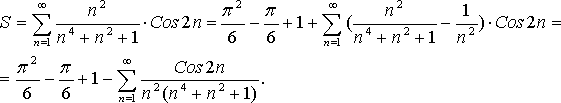
Определим количество членов полученного ряда, необходимое для обеспечения точности .
 .
.
Откуда находим, что k 10.
Таким образом,

Вычисление полученной суммы можно произвести на ЭВМ.
