ГОСКОМИТЕТ РОССИЙСКОЙ ФЕДЕРАЦИИ ПО ВЫСШЕМУ ОБРАЗОВАНИЮ

МОСКОВСКИЙ ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ ИНСТИТУТ

ЭЛЕКТРОННОЙ ТЕХНИКИ (ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)

"УТВЕРЖДАЮ"

Зав.кафедрой КФН

_____________ Горбацевич .А.А

“___"_________ 2009 г.

Лабораторная работа № 7

Определение характеристик структуры металл-полупроводник вольтфарадным методом

Авторы:

доцент Анфалова Е.С

Ст.преподаватель Бурзин С.Б.

Ведущий инженер Михалин В.В

МОСКВА 2009 г

Физика твердого тела и полупроводников

Лабораторная работа № 7

Определение характеристик структуры металл-полупроводник вольтфарадным методом

Вольтфарадный (C-V) метод широко используется для измерения электрофизических параметров структур металл-диэлектрик-полупроводник (МДП), диодов Шоттки, резких р-n переходов.

Метод основан на измерении емкости приповерхностной области полупроводника в зависимости от приложенного напряжения, обедняющего приповерхностный слой полупроводника основными носителями.

В настоящей работе измеряются C-V характеристики диодов Шоттки в структуре металл-полупроводник на основе арсенида галлия.

1. Контакт металл-полупроводник.

1.1. Образование контакта металл-полупроводник

Рассмотрим свойства идеального контакта металл-полупроводник. Предположим, что полупроводник не вырожден, на границе между полупроводником и металлом отсутствуют поверхностные состояния (ПС), полупроводник однородно легирован донорной примесью с концентрацией N_D и вся примесь ионизирована, последовательным сопротивлением подложки можно пренебречь.

Термодинамическая (или внутренняя) работа выхода электрона из твердого тела _S - это разница между энергией электрона в вакууме E₀ и энергией Ферми в твердом теле F_S. Внешняя работа выхода (или электронное сродство)  – это разность между энергией электрона в вакууме и энергией дна зоны проводимости Е_С. (рис.1(а)).

Термодинамическая работа выхода электрона из полупроводника определяется следующим соотношением.

,

(1)

где eVn = Е_C - F_S - разность между энергией дна зоны проводимости Е_C и уровнем Ферми F_S полупроводника.

Сродство к электрону  - это внутреннее свойство полупроводника, оно не изменяется при образовании контакта с металлом.

Обозначим работу выхода из металла _M. Если _M>_S, то при контакте металла и полупроводника часть электронов из полупроводника перейдет в металл, и на границе раздела образуется потенциальный барьер е_B (рис.1(6)), который называют барьером Шоттки, а структуру металл-полупроводник с таким барьером - диодом Шоттки.

При установлении термодинамического равновесия уровни Ферми в металле и полупроводнике совпадают, поэтому

.

(2)

Величина V_B=(_M - _S)/e - контактная разность потенциалов. Из (2) следует, что

.

(3)

Величина потенциального барьера зависит лишь от природы материалов контакта.

На рис.1(б) представлена энергетическая диаграмма барьера Шоттки при термодинамическом равновесии, то есть когда внешнее напряжение отсутствует (U=0). Энергетические диаграммы потенциального барьера при прямом (U>0) и обратном (U<0) смещениях на металлическом электроде изображены на рис.1(в) и 1(г), соответственно.

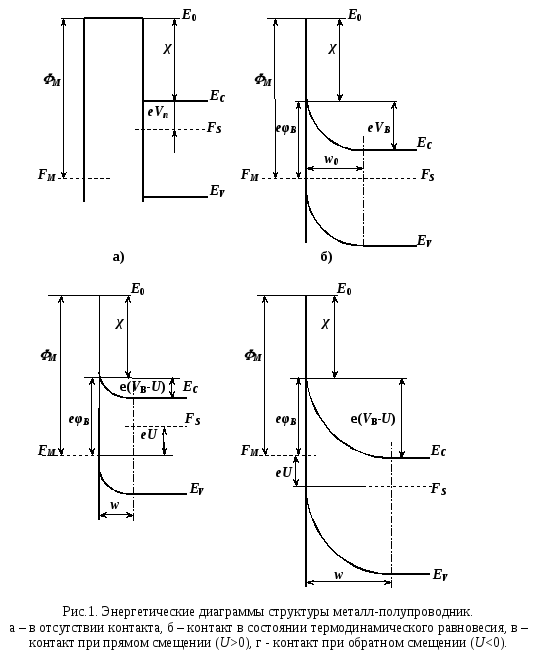
1.2. Область пространственного заряда

При наличии потенциального барьера е_B приповерхностная область полупроводника n-типа проводимости толщиной w обеднена электронами и заряжена положительно. Эта область называется областью пространственного заряда (ОПЗ). Потенциал V(x) в ОПЗ отрицателен и определяется уравнением Пуассона.

,

(4)

где  - диэлектрическая проницаемость полупроводника, ₀ - диэлектрическая постоянная, е=1.6∙10^-19 Кл – абсолютное значение заряда электрона, N_D - концентрация донорной примеси в полупроводнике; n(х) - концентрация свободных электронов в ОПЗ.

Полупроводник однородно легирован, тогда n₀=N_D, где n₀ - концентрация электронов в нейтральном объеме полупроводника. Для невырожденного полупроводника можно записать.

.

(5)

Тогда уравнение Пуассона (4) можно представить в следующем виде.

.

(6)

Будем искать решение, удовлетворяющее граничным условиям.

.

(6а)

Уравнение (6) удобно проинтегрировать по переменной V. Для этого умножим обе части уравнения на 2(dV/dx) и, используя тождество

,

представим уравнение (6) в следующем виде.

.

(7)

Проинтегрируем (7) и найдем

,

где A - постоянная интегрирования.

Из граничных условий (6а) следует, что , поэтому

.

(8)

Для потенциального барьера на границе (х=0) всегда выполняется условие . Поэтому в режиме обеднения (V(x)<0) выражение в квадратных скобках, оставаясь отрицательным, изменяется в области пространственного заряда от V_B+kT/e до нуля. Тогда уравнение (8) существенно упрощается.

,

(9)

Разделяя переменные x и V в (9) и интегрируя, получим

,

(10)

где x₀ - постоянная интегрирования, которую определим из (10) с помощью граничного условия V(0)=V_B.

.

(11)

Возведя обе части выражения (10) в квадрат и учитывая (11), получим

,

(11 а)

где тепловой потенциал В при комнатной температуре.

Пренебрегая величиной теплового потенциала _T по сравнению с V_B, запишем зависимость потенциала V от координаты х в ОПЗ следующим образом.

,

(11 б)

Из (11 6) найдем толщину w области пространственного заряда, на границе которой V(w)=0.

.

(11 в)

Если к структуре приложить внешнее напряжение U>0, то высота потенциального барьера со стороны полупроводника уменьшится, основные носители подтянутся к контакту, и толщина ОПЗ, согласно (11в), также уменьшится (рис.1(в)).

(12)

При обратном смещении U<0 ширина ОПЗ увеличивается (рис.1(г)).

Величина потенциального барьера eV_B снижается еще и за счет положительного заряда, индуцируемого полем электронов в ОПЗ полупроводника. Расчет методом "сил зеркального изображения" дает для величины понижения барьера е следующую величину.

,

(13)

где Е(0) – напряженность электрического поля на поверхности полупроводника. Величина  в S1 и GaAs мала. Так, в поле Е(0)1*10⁵ В/см она не превышает нескольких сотых вольта. В полях же, близких к пробивным (1*10⁶ В/см),  может составлять десятые доли вольта.