
- •1 Семестр
- •Глава 1. Пределы и непрерывность
- •§ 1.1. Числовые множества
- •1.1.1. Ограниченные множества
- •1.1.2. Точные грани множества
- •1.1.3. Существование точных граней
- •§ 1.2. Предел последовательности
- •Предельные точки и предел последовательности
- •Свойства предела последовательности
- •Арифметические свойства предела последовательности
- •Глава 2. Предел функции и непрерывность
- •§ 2.1. Предел функции в точке
- •Эквивалентные определения
- •2.1.2. Свойства предела функции в точке.
- •2.1.3. Арифметические свойства пределов
- •2.1.4. Критерий Коши существования предела
- •2.1.5. Односторонние пределы и пределы на бесконечности
- •§ 2.2. Непрерывность в точке и на отрезке
- •2.2.1. Непрерывность функции в точке
- •2.2.2. Первый замечательный предел
- •2.2.3. Второй замечательный предел
- •2.2.4. Бесконечно малые функции
- •2.2.5. Бесконечно большие функции
- •2.2.6. Классификация точек разрыва
- •2.2.7. Непрерывность функции на отрезке
§ 2.2. Непрерывность в точке и на отрезке
2.2.1. Непрерывность функции в точке
Определение.
Функция
![]() называетсянепрерывной
в точке
называетсянепрерывной
в точке
![]() если
если![]() то есть
то есть
![]()
Запишем определение
непрерывности на языке приращений.
Рассмотрим функцию
![]() определённую в некоторой окрестности
точки
определённую в некоторой окрестности
точки![]() и точку
и точку![]() из этой окрестности.Приращением
аргумента
называется
величина
из этой окрестности.Приращением
аргумента
называется
величина
![]() Приращению аргумента соответствует
приращение
функции
Приращению аргумента соответствует
приращение
функции
![]() Функция
Функция
![]() непрерывна в точке
непрерывна в точке![]() если
если![]()
Функция
![]() непрерывна
в точке
непрерывна
в точке![]() тогда и только тогда, когда в этой точке
существуют односторонние пределы,
равные значению в этой точке.
тогда и только тогда, когда в этой точке
существуют односторонние пределы,
равные значению в этой точке.
Если
![]() то функция называется непрерывной
справа
в точке
то функция называется непрерывной
справа
в точке
![]() если
если![]() тонепрерывной
слева.
тонепрерывной
слева.
Непрерывные в точке функций обладают всеми свойствами функций, имеющих предел в точке.
Теорема о
непрерывности сложной функции. Если
функция
![]() непрерывна в точке
непрерывна в точке![]() а
функция
а
функция![]() непрерывна в точке
непрерывна в точке![]() то сложная функция
то сложная функция![]() непрерывна в точке
непрерывна в точке![]()
Доказательство.
Зададим
![]() Так как функция
Так как функция![]() непрерывна в точке
непрерывна в точке![]() то найдётся
то найдётся![]() такое, что для всех
такое, что для всех![]() удовлетворяющих неравенству
удовлетворяющих неравенству![]() выполняется неравенство
выполняется неравенство![]() Так как функция
Так как функция![]() непрерывна в точке
непрерывна в точке![]() то для этого
то для этого![]() найдётся
найдётся![]() такое, что для всех
такое, что для всех![]() удовлетворяющих неравенству
удовлетворяющих неравенству![]() выполняется неравенство
выполняется неравенство![]() то есть
то есть![]() следовательно,
следовательно,![]() то есть
то есть![]() Значит,
Значит,![]() непрерывна в точке
непрерывна в точке![]()
Следствие. Если
![]()
![]() то
то![]()
Доказательство.
Рассмотрим
функции
![]() при
при![]()
![]() и
и
![]() при
при
![]()
![]() Так как функция
Так как функция
![]() непрерывна
в точке
непрерывна
в точке
![]() а функция
а функция![]() непрерывна в точке
непрерывна в точке![]() то функция
то функция
![]() непрерывна
в точке
непрерывна
в точке
![]()
![]()
Пример.
Функцию
![]() можно
рассматривать как сложную функцию
можно
рассматривать как сложную функцию![]() где
где![]()
![]() Ранее было доказано, что
Ранее было доказано, что![]()
![]() то есть функции
то есть функции![]() и
и![]() непрерывны в любой точке числовой
прямой. Тогда функция
непрерывны в любой точке числовой
прямой. Тогда функция![]() также непрерывна.
также непрерывна.
Из доказанных
свойств пределов и приведённых примеров
следует, что функции
![]()
![]() (
(![]() и
и![]() - многочлены),
- многочлены),![]()
![]() непрерывны во всех точках области
определения.
непрерывны во всех точках области
определения.
2.2.2. Первый замечательный предел
Теорема.
![]()
Доказательство.
Рассмотрим
![]() Можно считать, что
Можно считать, что
![]() По ранее доказанному неравенству имеем
По ранее доказанному неравенству имеем![]() Отметим
на единичной окружности точки
Отметим
на единичной окружности точки![]() и
и![]() соответствующие углам
соответствующие углам![]() и
и![]() и проведём из них касательные,
пересекающиеся в точке
и проведём из них касательные,
пересекающиеся в точке![]() лежащей на оси
лежащей на оси![]() Тогда длина дуги
Тогда длина дуги![]() равна
равна![]() и меньше дины ломаной
и меньше дины ломаной![]() равной
равной![]() то есть выполняется неравенство
то есть выполняется неравенство![]() Тогда получаем
Тогда получаем![]() Так как в силу непрерывности косинуса
Так как в силу непрерывности косинуса![]() то существует
то существует
![]() Рассмотрим теперь
Рассмотрим теперь
![]() Сделав замену
Сделав замену
![]() получим
получим
![]() Так как
односторонние пределы существуют и
равны между собой, то
Так как
односторонние пределы существуют и
равны между собой, то
![]()
Следствие. Если
![]() то
то
![]()
2.2.3. Второй замечательный предел
По определению
числа
![]() оно равно пределу последовательности
оно равно пределу последовательности![]() Однако, не для всякой функции
Однако, не для всякой функции![]() существование предела последовательности
существование предела последовательности![]() влечёт за собой существование предела
влечёт за собой существование предела![]() Например, для функции
Например, для функции![]() не существует предела при
не существует предела при![]() стремящемся к бесконечности, однако
последовательность
стремящемся к бесконечности, однако
последовательность![]() сходящаяся.
сходящаяся.
Теорема.
![]()
Доказательство.
Рассмотрим
сначала
![]() Можно
считать, что
Можно
считать, что
![]() Тогда
выполняются неравенства
Тогда
выполняются неравенства
![]() (
(![]() - целая часть
- целая часть![]() т.е. наибольшее целое число, не превосходящее
т.е. наибольшее целое число, не превосходящее![]() ).
Получаем
).
Получаем
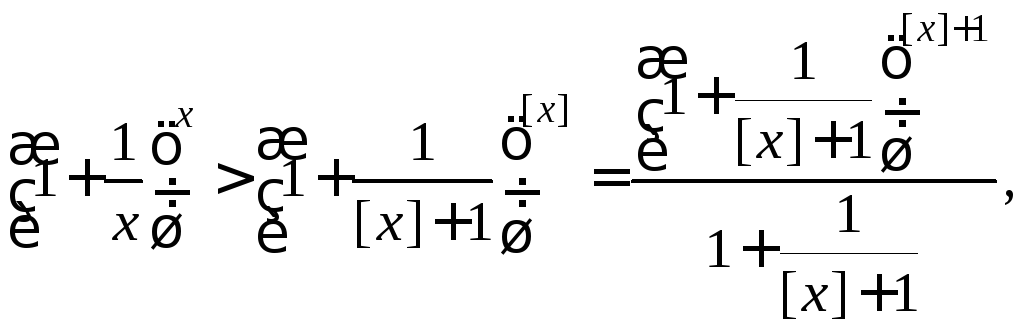
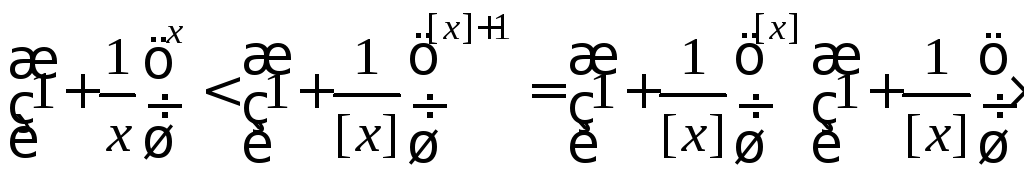
Так как
![]() и
и![]() натуральные, то
натуральные, то
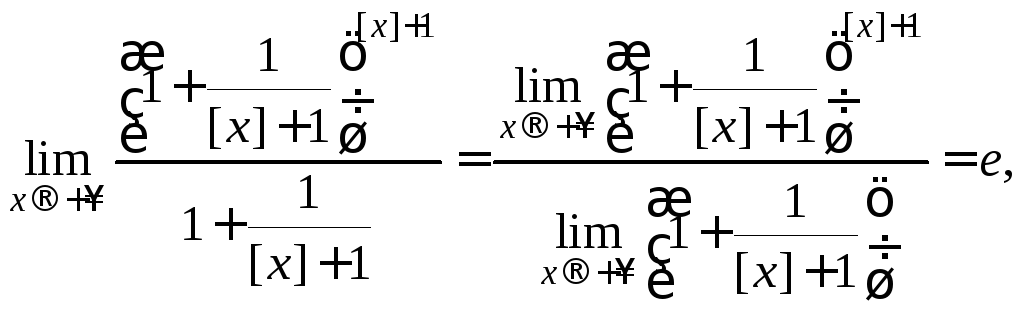
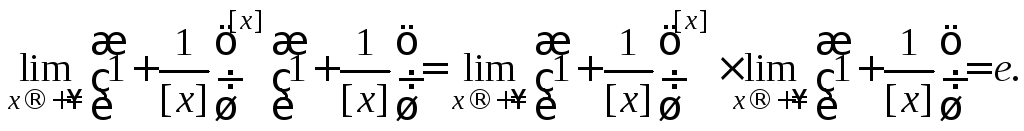 Следовательно,
Следовательно,
![]()
Рассмотрим
![]() сделав
замену
сделав
замену
![]()
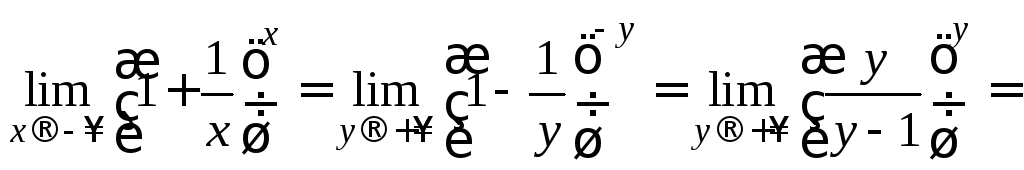
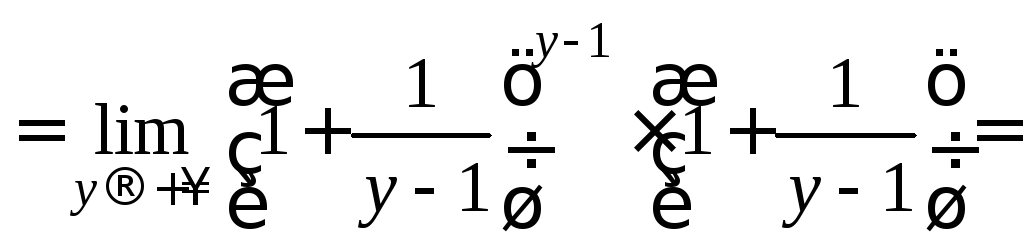

Следствия.
1. Если
![]() то
то![]()
2.
![]() 3.
3.![]()
4.
![]()
2.2.4. Бесконечно малые функции
Определение.
Функция
![]() называетсябесконечно
малой при
называетсябесконечно
малой при
![]() стремящемся к
стремящемся к![]() если
если![]()
Аналогично
определяются функции, бесконечно малые
при
![]() стремящемся к бесконечности.
стремящемся к бесконечности.
Утверждение.
![]() тогда и только тогда, когда функция
тогда и только тогда, когда функция![]() является бесконечно малой при
является бесконечно малой при![]() стремящемся к
стремящемся к![]()
Если
![]()
![]() - бесконечно малые при
- бесконечно малые при![]() то
то![]() также является бесконечно малой при
также является бесконечно малой при![]()
Если
![]() - бесконечно малая при
- бесконечно малая при![]() а
а![]() ограниченна в некоторой окрестности
точки
ограниченна в некоторой окрестности
точки![]() то
то![]() является бесконечно малой при
является бесконечно малой при![]()
Определение.
Две
функции
![]() и
и![]() являющиеся бесконечно малыми при
являющиеся бесконечно малыми при![]() называютсяэквивалентными
при
называютсяэквивалентными
при
![]() (
(![]() при
при![]() ),
если
),
если![]()
При
![]() справедливы следующие эквивалентности:
справедливы следующие эквивалентности:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Теорема. Если
![]() при
при![]() и существуют пределы
и существуют пределы![]()
![]() то существуют и пределы
то существуют и пределы![]()
![]()
Доказательство.
![]()
![]()
![]()
Если
![]() при
при![]() то
то![]() при
при![]()
Если
![]()
![]() при
при![]() то
то![]() при
при![]()
Пример. Вычислим
предел
![]() Так как при
Так как при![]() справедливы эквивалентности:
справедливы эквивалентности:
![]()
![]()
![]()
то

Определение.
Пусть даны
две
бесконечно
малые при
![]() функции
функции
![]() и
и![]() Порядком
малости
Порядком
малости
![]() относительно
относительно
![]() называется число
называется число![]() такое, что
такое, что![]() Если
Если![]() то говорят, что
то говорят, что
![]() является
бесконечно малой
большего порядка малости, чем
является
бесконечно малой
большего порядка малости, чем
![]() или
или
![]() является
о-малым
от
является
о-малым
от
![]() обозначается
обозначается
![]()
Теорема. Две
бесконечно
малые при
![]() функции
функции
![]() и
и![]() эквивалентны тогда и только тогда, когда
эквивалентны тогда и только тогда, когда![]()
Доказательство.
При
![]() равносильны утверждения:
равносильны утверждения:
![]()
![]()
![]()
Функции
![]() ,
бесконечно малые при
,
бесконечно малые при
![]() обычно
сравниваются с
обычно
сравниваются с
![]() Функции
Функции![]() ,
бесконечно малые при
,
бесконечно малые при
![]() сравниваются
с
сравниваются
с
![]()
Примеры.
1. Найдём
порядок бесконечно малой
![]() при
при
![]() относительно
относительно
![]()
![]() при
при
![]() порядок равен 3.
порядок равен 3.
2. Найдём порядок
бесконечно малой
![]() при
при
![]() относительно
относительно
![]()
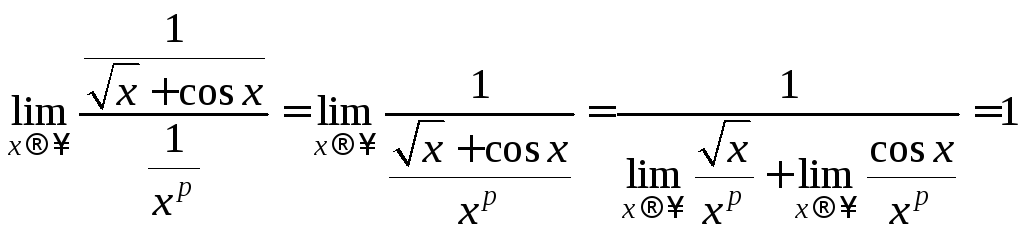
при
![]() т.к.
т.к.![]() как произведение бесконечно малой на
ограниченную. Порядок бесконечно малой
равен 0,5
как произведение бесконечно малой на
ограниченную. Порядок бесконечно малой
равен 0,5
