
7. Закон сохранения момента импульса Момент силы и момент импульса относительно неподвижной точки
 Важные
законы механики связаны с понятиями
момента силы и момента импульса. Пусть
на материальную точку
Важные
законы механики связаны с понятиями
момента силы и момента импульса. Пусть
на материальную точку
![]() ,
положение которой относительно
неподвижной точки
,
положение которой относительно
неподвижной точки![]() определяется радиус-вектором
определяется радиус-вектором![]() (рис. 1), действует сила
(рис. 1), действует сила![]() Моментом
силы
Моментом
силы
![]() относительно точки
относительно точки![]() называют вектор
называют вектор![]() равный
векторному произведению векторов
равный
векторному произведению векторов![]() и
и![]()
![]() .
(1)
.
(1)
Модуль вектора
![]() равен
равен
![]()
где
![]() – угол между векторами
– угол между векторами![]() и
и![]()
![]() –плечо
силы относительно точки
–плечо
силы относительно точки
![]() (плечо силы – это кратчайшее расстояние
между точкой
(плечо силы – это кратчайшее расстояние
между точкой![]() и линией действия силы). Отсюда
непосредственно следует, что момент
силы не изменится, если точку приложения
силы перенести в любую другую точку,
расположенную на линии действия силы,
например, в точку, положение которой
определяется радиус-вектором
и линией действия силы). Отсюда
непосредственно следует, что момент
силы не изменится, если точку приложения
силы перенести в любую другую точку,
расположенную на линии действия силы,
например, в точку, положение которой
определяется радиус-вектором![]() (см. рис. 1).
(см. рис. 1).
Аналогично
определяется момент
импульса
![]() относительно точки
относительно точки![]()
![]() ,
(2)
,
(2)
где
![]() – импульс материальной точки.
Продифференцируем по времени последнее
выражение
– импульс материальной точки.
Продифференцируем по времени последнее
выражение
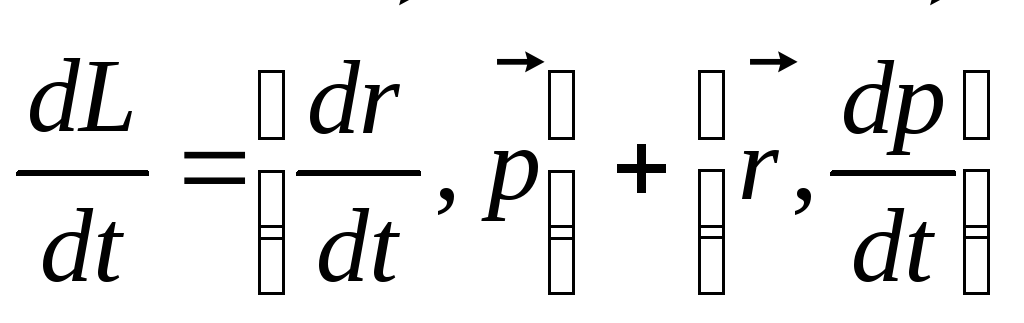 .
(3)
.
(3)
Импульс
![]() материальной точки
материальной точки![]() коллинеарен с ее скоростью
коллинеарен с ее скоростью![]() ,
поэтому первое векторное произведение
в уравнении (3) равно нулю. Учитывая, что
,
поэтому первое векторное произведение
в уравнении (3) равно нулю. Учитывая, что![]() ,
уравнение (3) принимает вид
,
уравнение (3) принимает вид
![]() (4)
(4)
Это уравнение называется уравнением моментов для одной материальной точки.
Рассмотрим систему
материальных точек. Запишем уравнение
(4) для каждой материальной точки, понимая
теперь под
![]() момент как внешних, так и внутренних
сил, действующих на рассматриваемую
точку. Затем сложим все эти уравнения
момент как внешних, так и внутренних
сил, действующих на рассматриваемую
точку. Затем сложим все эти уравнения
![]() ,
,
где
![]() – момент всех внешних сил, действующих
на систему, а
– момент всех внешних сил, действующих
на систему, а![]() – момент всех внутренних сил. Внутренние
силы входят в систему попарно: сила
– момент всех внутренних сил. Внутренние
силы входят в систему попарно: сила![]() ,
с которой
,
с которой![]() -я
точка действует на
-я
точка действует на![]() -ю,
равна силе
-ю,
равна силе![]() ,
с которой
,
с которой![]() -я
точка действует на
-я
точка действует на![]() -ю.
Эти силы направлены в противоположные
стороны и действуют вдоль одной и той
же прямой. Суммарный момент таких двух
сил, а значит и суммарный момент всех
внутренних сил равен нулю. В результате
получаемуравнение
моментов для
системы материальных точек
-ю.
Эти силы направлены в противоположные
стороны и действуют вдоль одной и той
же прямой. Суммарный момент таких двух
сил, а значит и суммарный момент всех
внутренних сил равен нулю. В результате
получаемуравнение
моментов для
системы материальных точек
![]() ,
(5)
,
(5)
т.е. производная момента импульса системы по времени равна суммарному моменту всех внешних сил.
Если
момент внешних сил относительно
неподвижной точки
![]() равен
нулю, то
момент импульса системы относительно
той же точки остается постоянным во
времени. Это
положение называется законом
сохранения момента импульса относительно
неподвижной точки .
равен
нулю, то
момент импульса системы относительно
той же точки остается постоянным во
времени. Это
положение называется законом
сохранения момента импульса относительно
неподвижной точки .
Уравнение моментов относительно неподвижной оси
Под уравнением
моментов относительно неподвижной оси
понимают проекцию уравнения моментов
(5) относительно неподвижной точки
![]() на ось
на ось
![]() ,
проходящую через эту точку
,
проходящую через эту точку
![]() ,
(6)
,
(6)
где
![]() –
алгебраическая сумма проекций моментов
импульса каждой материальной точки на
ось
–
алгебраическая сумма проекций моментов
импульса каждой материальной точки на
ось![]()
![]() –
алгебраическая сумма проекций на ось
–
алгебраическая сумма проекций на ось![]() моментов внешних сил, действующих на
данную систему материальных точек.
моментов внешних сил, действующих на
данную систему материальных точек.
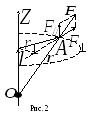 Для
того чтобы понять смысл величин, входящих
в уравнение (6), рассмотрим сначала одну
материальную точку
Для
того чтобы понять смысл величин, входящих
в уравнение (6), рассмотрим сначала одну
материальную точку![]() ,
на которую действует сила
,
на которую действует сила![]() Представим радиус-вектор
Представим радиус-вектор![]() определяющий положение точки
определяющий положение точки![]() относительно точки
относительно точки
![]() в виде суммы двух векторов (рис. 2)
в виде суммы двух векторов (рис. 2)
![]() (7)
(7)
где
![]() – вектор, параллельный оси
– вектор, параллельный оси![]() ,
а
,
а![]() – вектор, перпендикулярный оси
– вектор, перпендикулярный оси![]()
Силу
![]() также представим в виде суммы двух
векторов
также представим в виде суммы двух
векторов
![]() (8)
(8)
где
![]() – направлена вдоль оси
– направлена вдоль оси![]() а
а![]() –лежит
в плоскости, перпендикулярной оси
–лежит
в плоскости, перпендикулярной оси
![]() Подставляя (7) и (8) в уравнение (1) и делая
несложные преобразования, получим
Подставляя (7) и (8) в уравнение (1) и делая
несложные преобразования, получим
![]() .
(9)
.
(9)
Первое
векторное произведение равно нулю, т.к.
![]() и
и
![]() коллинеарныевектора.
Векторы, представляющие второе и третье
векторные произведения, перпендикулярны
оси
коллинеарныевектора.
Векторы, представляющие второе и третье
векторные произведения, перпендикулярны
оси
![]() поэтому проекции этих векторов на эту
ось равны нулю. Таким образом, составляющая
вектора
поэтому проекции этих векторов на эту
ось равны нулю. Таким образом, составляющая
вектора![]() параллельная
оси
параллельная
оси![]() равна
равна
![]() .
.
Только
эта составляющая и играет роль при
нахождении момента силы на ось
![]() .
Модуль этого вектора равен
.
Модуль этого вектора равен
![]()
где
![]() – плечо силы
– плечо силы![]() относительно оси
относительно оси![]() (плечо
силы относительно оси – это кратчайшее
расстояние от линии действия силы
(плечо
силы относительно оси – это кратчайшее
расстояние от линии действия силы![]() до оси
до оси![]() ).
).
Проводя
аналогичные рассуждения для момента
импульса
![]() ,
получим
,
получим
![]()
где
![]() – проекция импульса материальной точки
– проекция импульса материальной точки![]() на плоскость, перпендикулярную оси
на плоскость, перпендикулярную оси![]() .
.
Распространяя этот результат на систему материальных точек, получим
![]()
![]()
Напомним,
что
![]() – это момент внешних сил, действующих
на систему.
– это момент внешних сил, действующих
на систему.
