
- •1. Дифференциальные уравнения 1-го порядка
- •1.1. Дифференциальные уравнения семейства кривых
- •1.2. Дифференциальные уравнения с разделяющимися переменными
- •1.3. Однородные дифференциальные уравнения
- •1.4. Линейные дифференциальные уравнения
- •1.5. Дифференциальное уравнение Бернулли
- •1.6. Дифференциальные уравнения в полных дифференциалах
- •1.7. Нахождение уравнений кривых с помощью дифференциальных уравнений 1-го порядка
- •1.8. Применение дифференциальных уравнений 1-го порядка для решения задач физики и химии
- •Справочный материал
- •1.8.1. Дополнительные задачи.
- •1.9. Уравнения Лагранжа и Клеро
1.9. Уравнения Лагранжа и Клеро
Уравнения
Лагранжа и Клеро относят к типу
дифференциальных уравнений, не разрешённых
относительно производной
![]() .
.
Уравнение
Лагранжа.
Стандартная форма записи уравнения:
![]() .
Для решения таких уравнений разработан
специальный способ – поиск решенияв
параметрической форме:
.
Для решения таких уравнений разработан
специальный способ – поиск решенияв
параметрической форме:
1. Полагают![]() =
=![]() и записывают исходное уравнение в
виде
и записывают исходное уравнение в
виде![]() .
.
2. Дифференцируют
выражение
![]() по переменной
по переменной![]() :
:![]() .
Заменяя
.
Заменяя![]() на
на![]() ,
получают:
,
получают:
![]() . (1.24)
. (1.24)
3. Если уравнение
![]() имеет корни
имеет корни![]() ,
то функции
,
то функции![]() будут решениями уравнения (1.24), а прямые
будут решениями уравнения (1.24), а прямые![]() решениями уравнения Лагранжа.
решениями уравнения Лагранжа.
4. Если
![]() ,
то уравнение (1.24) записывают как линейное
относительно переменной
,
то уравнение (1.24) записывают как линейное
относительно переменной![]()
![]() –
–![]() =
=![]() .
Найдя его решение
.
Найдя его решение![]() и, составив систему
и, составив систему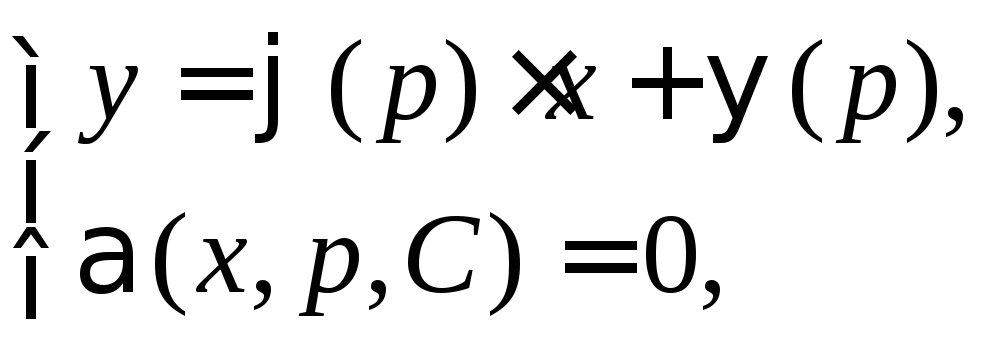 получают решение
уравнения Лагранжа в параметрическом
виде.
получают решение
уравнения Лагранжа в параметрическом
виде.
Пример 1.9.Найти
общее решение уравнения Лагранжа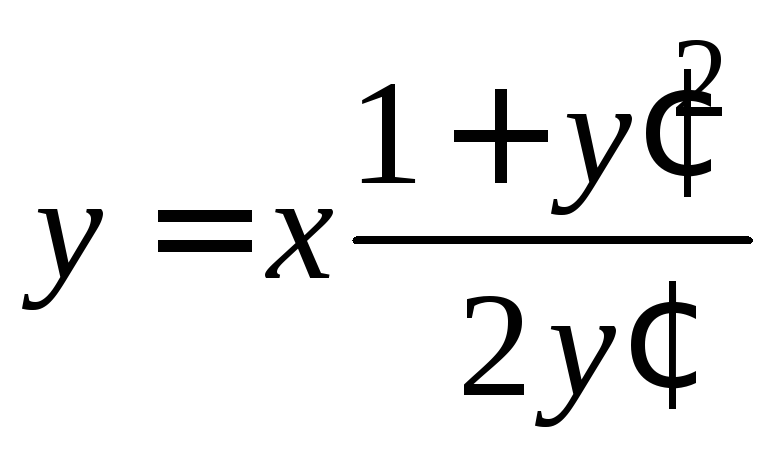 в параметрической форме.
в параметрической форме.
Решение.1)
Запишем уравнение в стандартном виде
![]() ,
где
,
где![]() =
=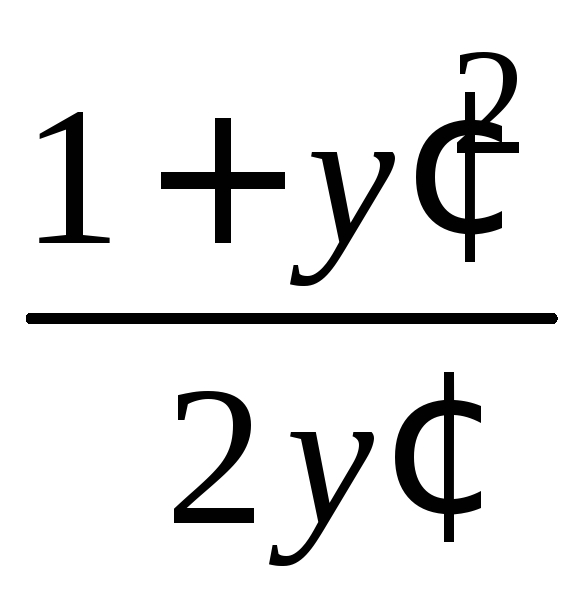 и
и![]() = 0.
Полагаем
= 0.
Полагаем![]() =
=![]() .
Перепишем исходное уравнение
.
Перепишем исходное уравнение![]() =
=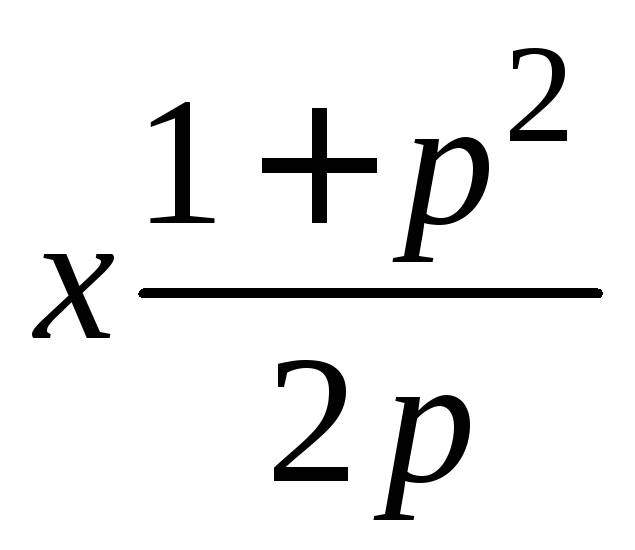 .
.
2) Дифференцируем
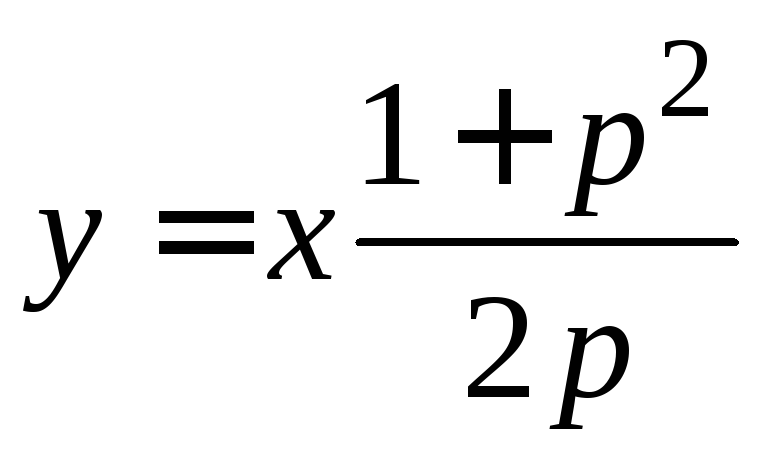 по переменной
по переменной![]()
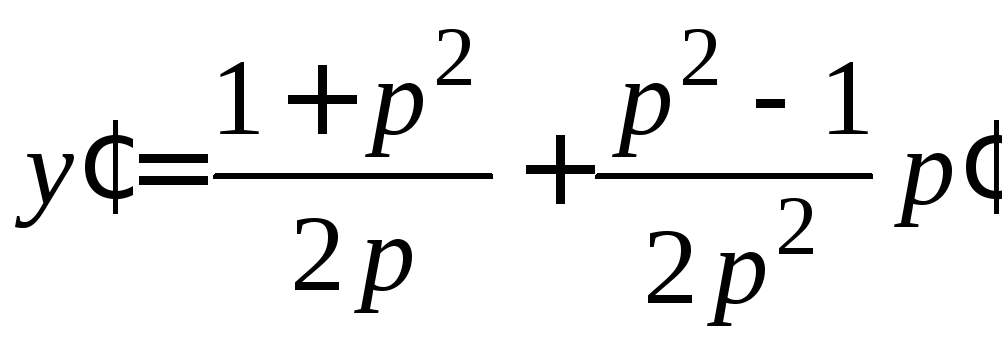 .
Заменяя
.
Заменяя![]() на
на![]() получим
получим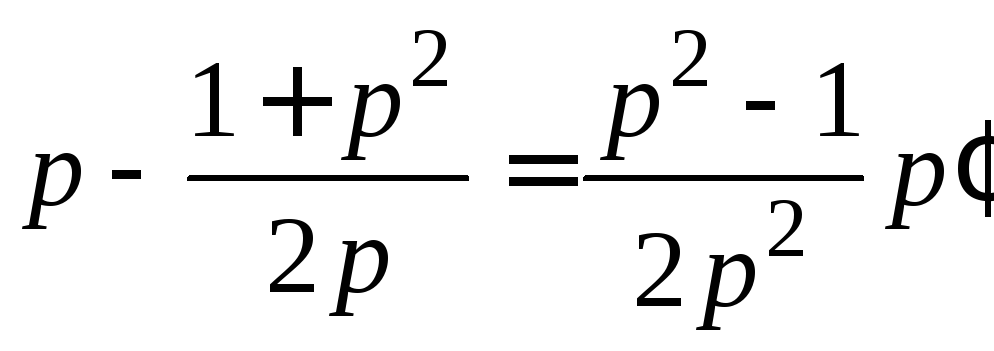 .
.
3) Уравнение
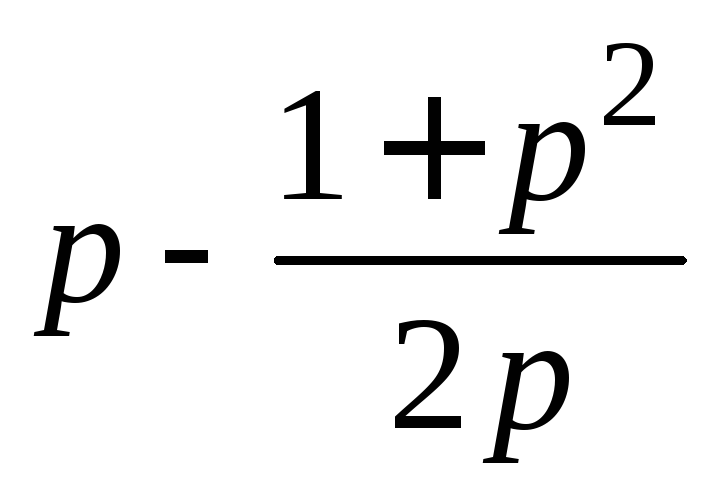 =0
имеет корни
=0
имеет корни![]() = –1
и
= –1
и![]() = 1.
Следовательно, функции
= 1.
Следовательно, функции![]() и
и![]() ,
то есть
,
то есть![]() =
=![]() и
и![]() =
=![]() являются решениями исходного уравнения.
являются решениями исходного уравнения.
4) В случае
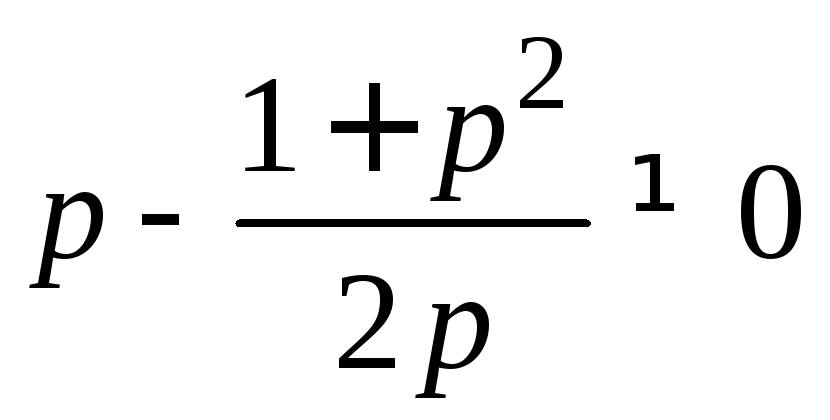 ,
учитывая, что
,
учитывая, что![]() =
=![]() ,
после простых преобразований уравнение
,
после простых преобразований уравнение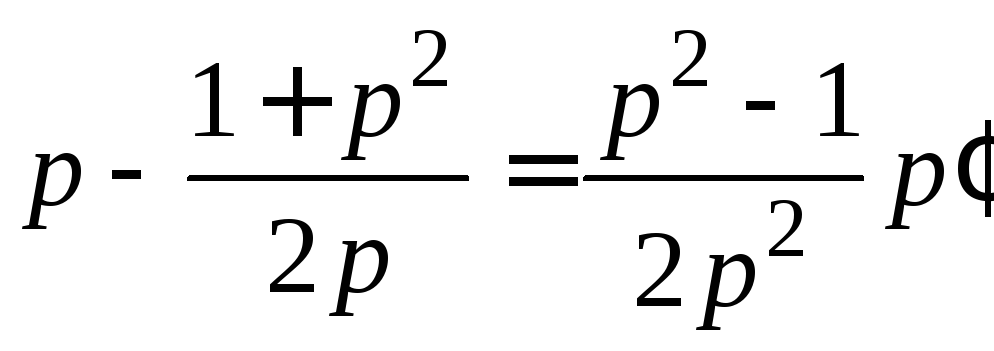 перепишем в виде линейного уравнения
относительно
перепишем в виде линейного уравнения
относительно![]()
![]() =
=![]() .
Откуда
.
Откуда![]() .
.
5) Составим систему
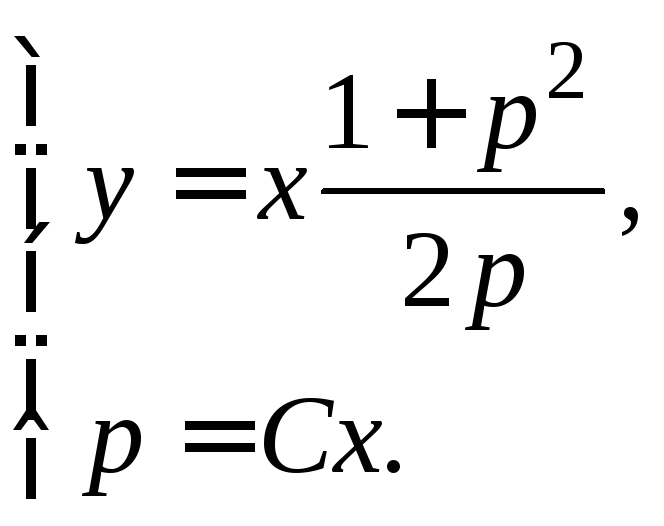 – решение уравнения Лагранжа
в параметрической форме, из которой
легко получить решение в явном виде
– решение уравнения Лагранжа
в параметрической форме, из которой
легко получить решение в явном виде![]() .
.
Ответ.
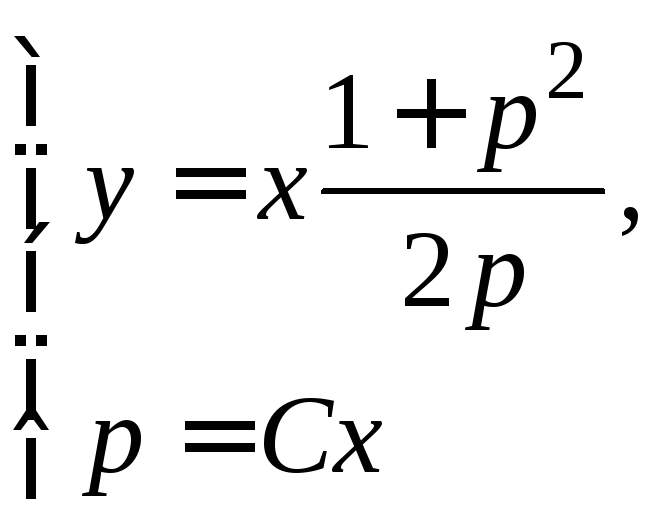 или
или
![]() ;
;
![]() .
.
Задание 1.9. Решить уравнения Лагранжа.
|
Вар. |
Уравнение: |
Вар. |
Уравнение: |
|
1.9.1. |
|
1.9.4. |
|
|
1.9.2. |
|
1.9.5. |
|
|
1.9.3. |
|
1.9.6. |
|
Уравнение
Клеро.
Стандартная форма записи уравнения
![]() .
Уравнение Клеро является частным случаем
уравнения Лагранжа. Решение его ищут,
как и уравнения Лагранжа,
в параметрической форме.
.
Уравнение Клеро является частным случаем
уравнения Лагранжа. Решение его ищут,
как и уравнения Лагранжа,
в параметрической форме.
Пример 1.10.Решить уравнение Клеро![]() ,
применяя метод введения параметра.
,
применяя метод введения параметра.
Решение.1)
Полагая![]() =
=![]() и дифференцируя выражение
и дифференцируя выражение![]() ,
получим уравнение
,
получим уравнение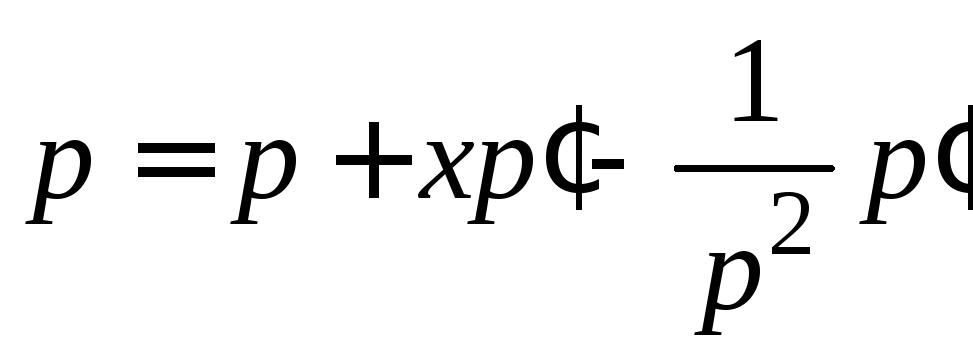 или
или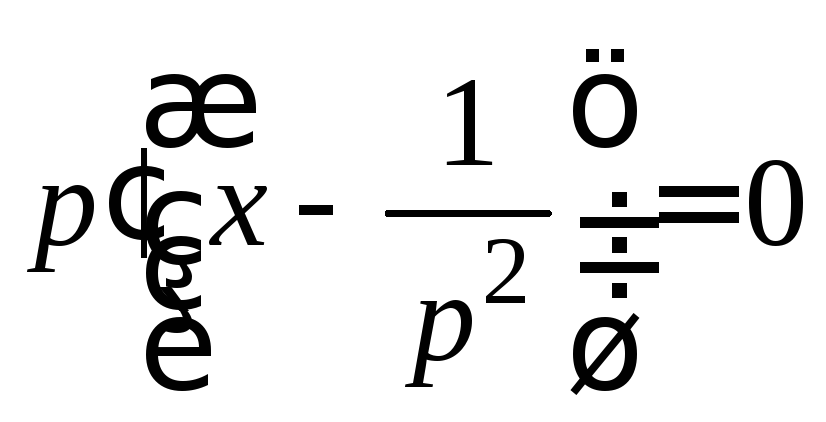 .
.
2 )
Пусть
)
Пусть![]() .
Тогда
.
Тогда![]() и получаем следующее решение уравнения
Клеро в параметрической форме
и получаем следующее решение уравнения
Клеро в параметрической форме
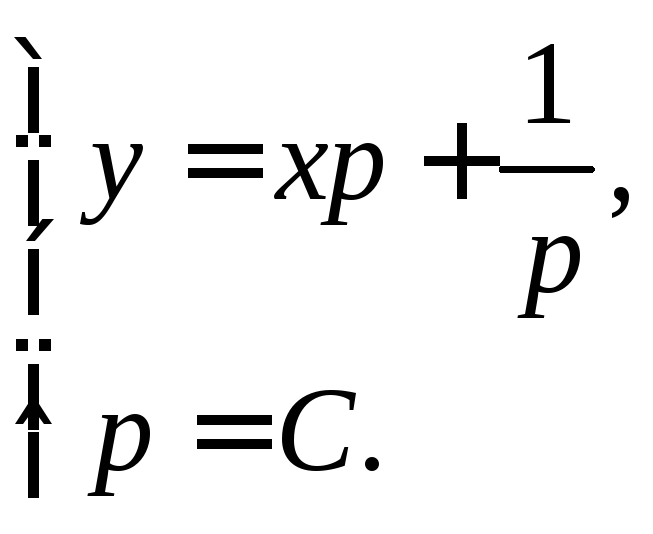 Исключая
Исключая![]() ,
найдем решение в явном виде
,
найдем решение в явном виде![]() .
Это решение задает одно параметрическое
семейство прямых.
.
Это решение задает одно параметрическое
семейство прямых.
3) Пусть
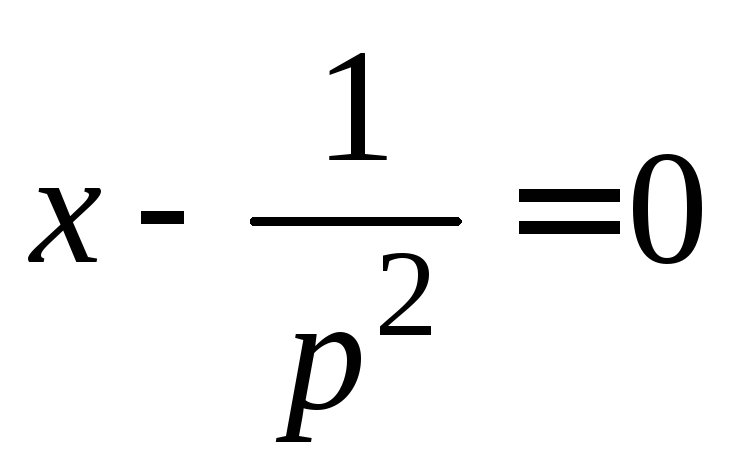 .
В этом случае получаем, что решением
является линия
.
В этом случае получаем, что решением
является линия
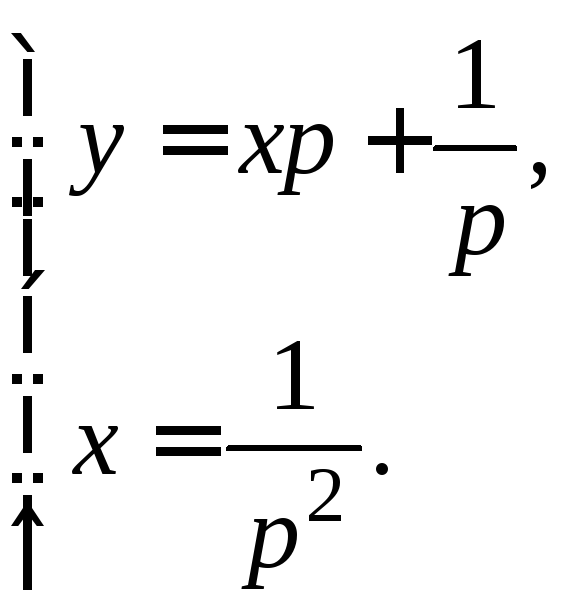 Исключая параметр
Исключая параметр![]() ,
получим решение в явном виде
,
получим решение в явном виде![]() – парабола. Данная парабола является
огибающей семейства
– парабола. Данная парабола является
огибающей семейства![]() (то есть в каждой своей точке касается
одной из прямых семейства (см.рис.1.8)) и
задаетособоерешение исходного
уравнения (решение особое, если через
каждую его точку проходит более одного
решения дифференциального уравнения).
(то есть в каждой своей точке касается
одной из прямых семейства (см.рис.1.8)) и
задаетособоерешение исходного
уравнения (решение особое, если через
каждую его точку проходит более одного
решения дифференциального уравнения).
Ответ.![]() ,
особое решение:
,
особое решение:![]() .
.
Задание 1.10. Решить уравнения Клеро.
|
Вар. |
Уравнение: |
Вар. |
Уравнение: |
|
1.10.1. |
|
1.10.4. |
|
|
1.10.2. |
|
1.10.5. |
|
|
1.10.3. |
|
1.10.6. |
|
