
- •1. Дифференциальные уравнения 1-го порядка
- •1.1. Дифференциальные уравнения семейства кривых
- •1.2. Дифференциальные уравнения с разделяющимися переменными
- •1.3. Однородные дифференциальные уравнения
- •1.4. Линейные дифференциальные уравнения
- •1.5. Дифференциальное уравнение Бернулли
- •1.6. Дифференциальные уравнения в полных дифференциалах
- •1.7. Нахождение уравнений кривых с помощью дифференциальных уравнений 1-го порядка
- •1.8. Применение дифференциальных уравнений 1-го порядка для решения задач физики и химии
- •Справочный материал
- •1.8.1. Дополнительные задачи.
- •1.9. Уравнения Лагранжа и Клеро
1.8. Применение дифференциальных уравнений 1-го порядка для решения задач физики и химии
Для составления дифференциального уравнения – математической модели физической (химической) задачи – часто применяют следующие способы:
1) записывают условие на производную искомой величины, используя известные законы физики и физический смысл производной;
2) определяют, какая
из величин будет независимой переменной
(обозначим её x), а
какая зависимой (обозначим еёy);
затем, используя соотношения между
нужными величинами при постоянных
значениях параметров, находят линейное
приближение для приращения![]() когда независимая переменная получила
приращение
когда независимая переменная получила
приращение![]() ;
разделив
;
разделив![]() на
на![]() и переходя к пределу при
и переходя к пределу при![]() ,
получают дифференциальное уравнение.
,
получают дифференциальное уравнение.
Для правильного составления уравнений требуется знание физических законов (первый и второй законы Ньютона, законы Кирхгофа для цепи переменного тока, закон Ньютона для скорости изменения температуры тела (см. указание 3 к заданию 1.8 и некоторые другие) в рамках стандартного курса общей физики по разделам: механика, термодинамика и молекулярная физика, электричество и магнетизм.
Справочный материал
Закон гравитации.
Сила притяжения двух точечных (или
сферически симметричных) масс![]() и
и![]() ,
находящихся на расстоянии
,
находящихся на расстоянии![]() друг от друга:
друг от друга:
![]() ,
,
где
![]() (в системе СИ) – гравитационная постоянная.
(в системе СИ) – гравитационная постоянная.
Уравнение состояния идеального газа
![]() ,
,
где
![]() – давление,
– давление,![]() – объём,
– объём,![]() – абсолютная
температура,
– абсолютная
температура,![]() – молярная
масса,
– молярная
масса,![]()
![]() – универсальная газовая постоянная.
– универсальная газовая постоянная.
Закон Кулона.
Сила взаимодействия двух точечных
(или сферически симметричных) зарядов![]() и
и![]() ,
находящихся на расстоянии
,
находящихся на расстоянии![]() друг от друга:
друг от друга:
![]() ,
,
где
![]() (в системе СИ) – постоянная закона
Кулона. Также постоянную
(в системе СИ) – постоянная закона
Кулона. Также постоянную![]() записывают в виде
записывают в виде![]() ,
где
,
где![]() – электрическая постоянная.
– электрическая постоянная.
Сила, действующая на точечный заряд в электрическом поле
![]() ,
,
где
![]() – напряжённость электрического поля
в точке, где расположен заряд.
– напряжённость электрического поля
в точке, где расположен заряд.
Закон Ома связывает
силу тока![]() ,
протекающего через проводник сопротивлением
,
протекающего через проводник сопротивлением![]() ,
и напряжение (разность потенциалов)
,
и напряжение (разность потенциалов)![]() на концах этого проводника
на концах этого проводника
![]() .
.
Электрический конденсатор (ёмкость)
![]() ,
,
где
![]() – ёмкость конденсатора,
– ёмкость конденсатора,![]() – заряд конденсатора,
– заряд конденсатора,![]() – напряжение между обкладками
конденсатора.
– напряжение между обкладками
конденсатора.
Потенциальная энергия конденсатора
![]() .
.
Плоский конденсатор
![]() ,
,
где
![]() – площадь каждой пластины (обкладки)
конденсатора,
– площадь каждой пластины (обкладки)
конденсатора,![]() – расстояние между пластинами,
– расстояние между пластинами,![]() – диэлектрическая проницаемость среды,
заполняющей пространство между
пластинами.
– диэлектрическая проницаемость среды,
заполняющей пространство между
пластинами.
Напряжённость электрического поля между пластинами плоского конденсатора
![]() .
.
Сила притяжения пластин плоского конденсатора между собой
![]() ,
,
где
![]() – заряд конденсатора,
– заряд конденсатора,![]() – напряжённость электрического поля
в конденсаторе.
– напряжённость электрического поля
в конденсаторе.
Механический момент, действующий на электрический диполь в однородном электрическом поле
![]() ,
,
где
![]() – вектор дипольного момента,
– вектор дипольного момента,![]() – модуль зарядов диполя,
– модуль зарядов диполя,![]() – вектор, направленный из точки зарядом
– вектор, направленный из точки зарядом![]() в точку с зарядом
в точку с зарядом![]() .
.
П ример
1.8.Чаша в форме параболоида вращения
в начальный момент заполнена водой. В
самой нижней части чаши имеется отверстие
радиуса
ример
1.8.Чаша в форме параболоида вращения
в начальный момент заполнена водой. В
самой нижней части чаши имеется отверстие
радиуса![]() ,
через которое вытекает вода (рис.1.5).
Найти зависимость
,
через которое вытекает вода (рис.1.5).
Найти зависимость![]() уровня воды в чаше от времени, если
высота чаши
уровня воды в чаше от времени, если
высота чаши![]() ,
радиус верхнего края
,
радиус верхнего края![]() .
За какой промежуток времени
.
За какой промежуток времени![]() из чаши вытечет вся вода?
из чаши вытечет вся вода?
Решение.Зависимость между уровнем![]() воды в чаше и радиусом
воды в чаше и радиусом![]() горизонтальной поверхности воды имеет
вид
горизонтальной поверхности воды имеет
вид
![]() .
.
Пусть за промежуток
времени
![]() уровень воды изменится на
уровень воды изменится на![]() (рис.1.5), тогда изменение объёма воды в
чаше
(рис.1.5), тогда изменение объёма воды в
чаше
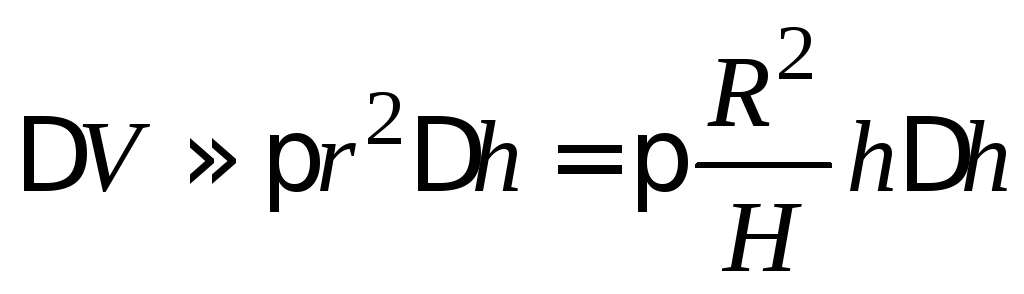 . (1.15)
. (1.15)
С другой стороны, это изменение равно
![]() ,
(1.16)
,
(1.16)
где
![]() –
скорость истечения воды из отверстия
(см. Указание 1 к решению задач).
–
скорость истечения воды из отверстия
(см. Указание 1 к решению задач).
Приравнивая (1.15)
и (1.16) и переходя к пределу при
![]() ,
получим дифференциальное уравнение
,
получим дифференциальное уравнение
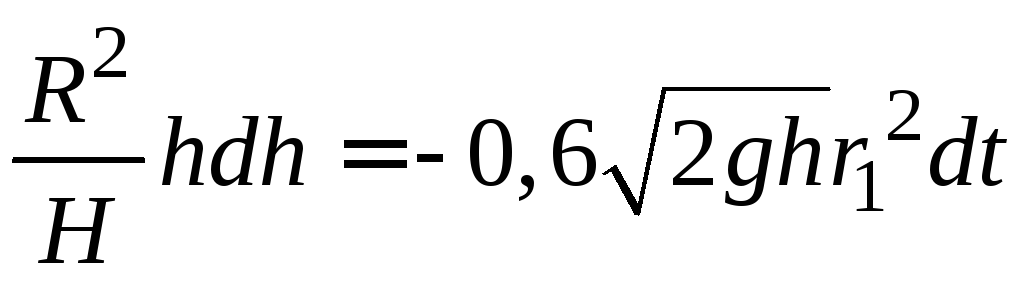 .
(1.17)
.
(1.17)
После разделения переменных в (1.17) и интегрирования, имеем:
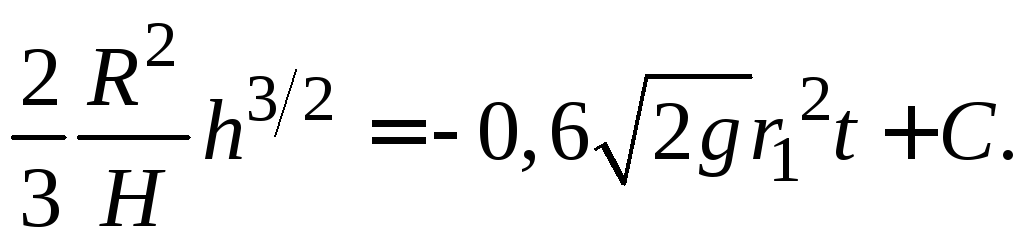 (1.18)
(1.18)
Найдём константу
![]() из начальных условий. Так как
из начальных условий. Так как![]() ,
то
,
то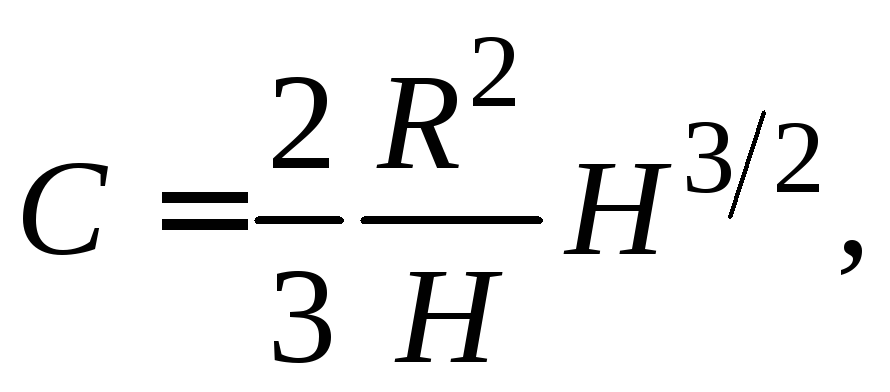 поэтому (1.18) примет вид
поэтому (1.18) примет вид
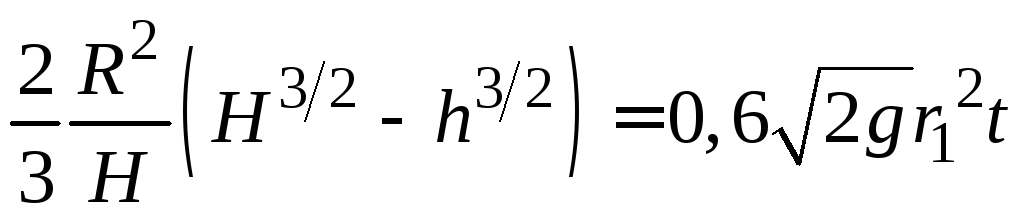 .
(1.19)
.
(1.19)
Выражая
![]() из (1.19), получим искомую зависимость:
из (1.19), получим искомую зависимость:
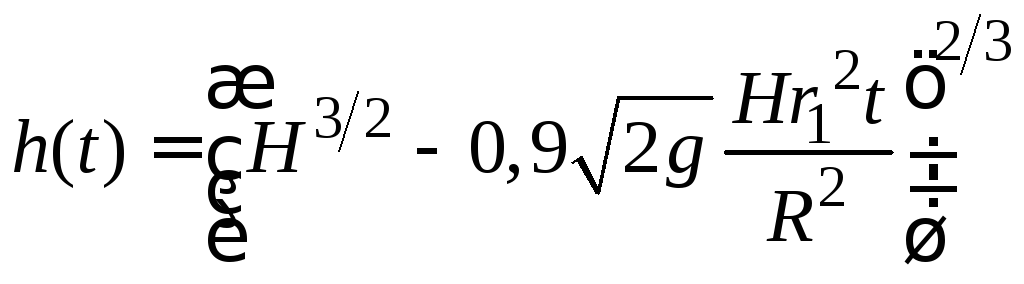 .
.
Поскольку
![]() ,
то из (1.19) найдём время, за которое вытечет
вся вода:
,
то из (1.19) найдём время, за которое вытечет
вся вода:
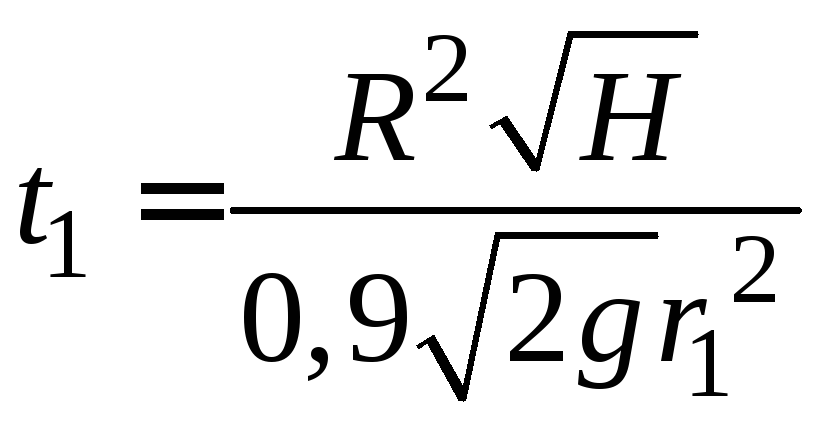 .
.
Задание 1.8. Решить задачи.
Указание 1.
В задачах 1.8.13-1.8.20 принять, что жидкость
с учётом вязкости вытекает из сосуда
со скоростью![]() ,
где
,
где![]() – высота уровня воды над отверстием.
– высота уровня воды над отверстием.
Указание 2:В задачах 1.8.27, 1.8.29, Д3 – Д5, Д8, Д9 производные![]() (или
(или![]() )
следует выразить как производные сложной
функции
)
следует выразить как производные сложной
функции![]() (или
(или![]() )
через
)
через![]() и
и![]() (или через
(или через![]() и
и![]() ).
).
Указание 3.В задачах 1.8.6, 1.8.7 считать, что скорость изменения температуры тела пропорциональна разности между температурой окружающей среды и температурой этого тела.
Пуля массой
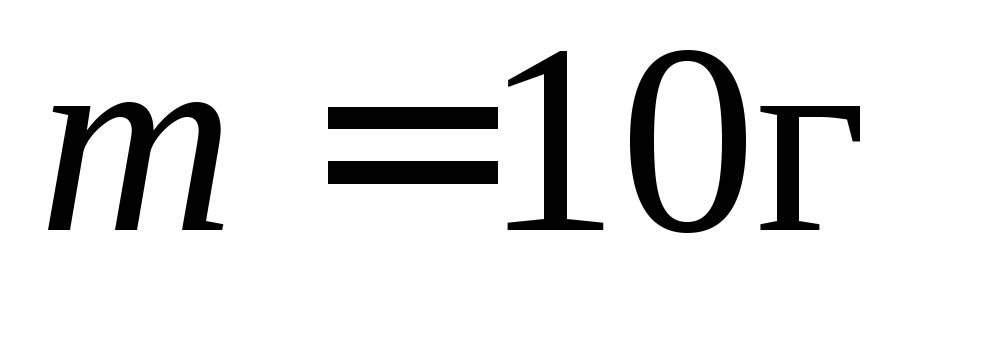 летящая
со скоростью
летящая
со скоростью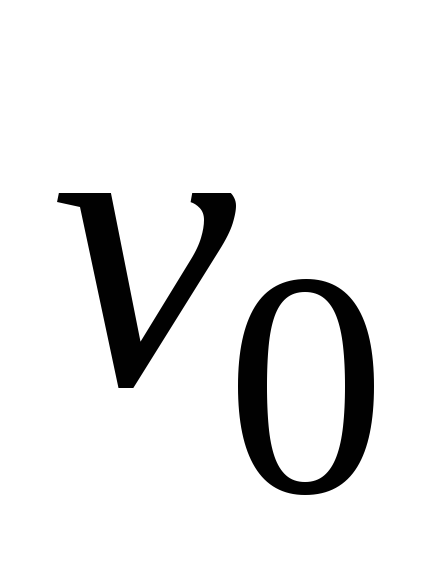 = 200 м/c,
пробивает доску за
= 200 м/c,
пробивает доску за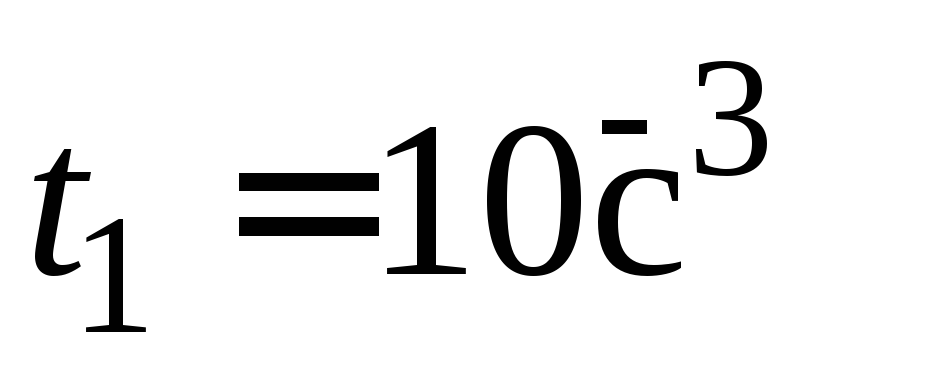 .
Найти скорость пули
.
Найти скорость пули после вылета из доски, если внутри
доски сила сопротивления пропорциональна
квадрату скорости пули с коэффициентом
после вылета из доски, если внутри
доски сила сопротивления пропорциональна
квадрату скорости пули с коэффициентом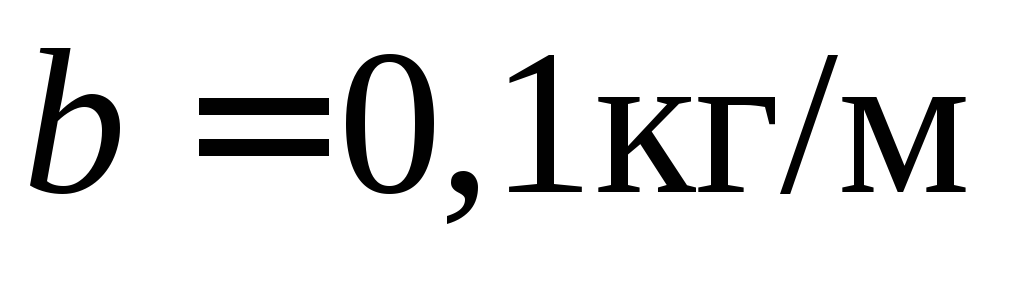 .
Найти также толщину
.
Найти также толщину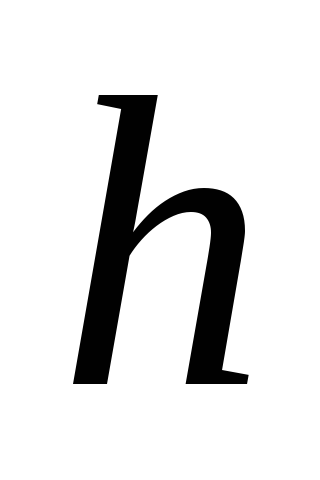 доски.
доски.
Лодка замедляет свое движение под действием сопротивления воды, которое пропорционально скорости лодки. Начальная скорость лодки
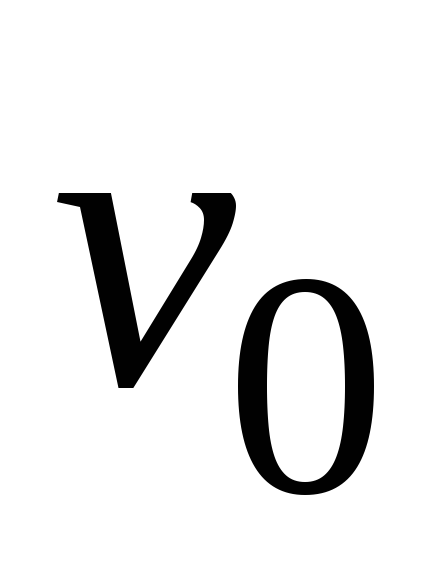 = 1,5 м/с,
через
= 1,5 м/с,
через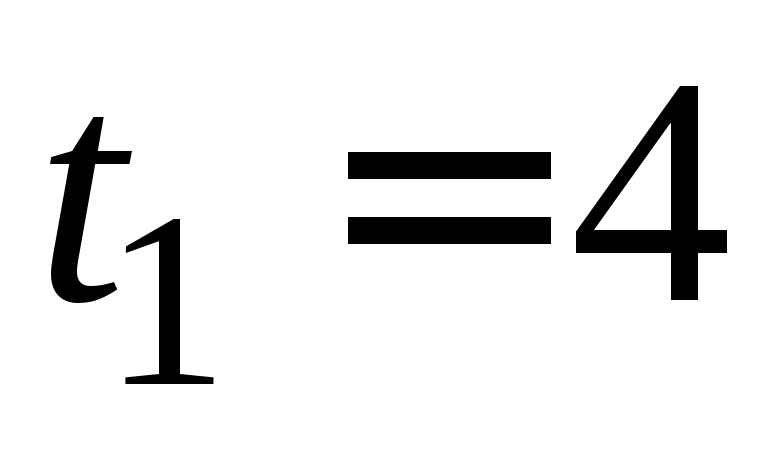 с
скорость ее стала
с
скорость ее стала = 1 м/с.
В какой момент
= 1 м/с.
В какой момент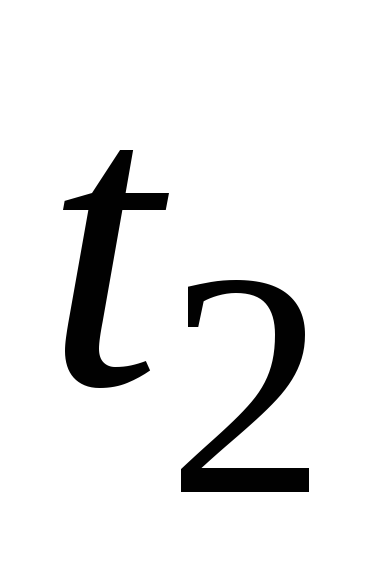 времени после начала торможения
скорость лодки будет равна
времени после начала торможения
скорость лодки будет равна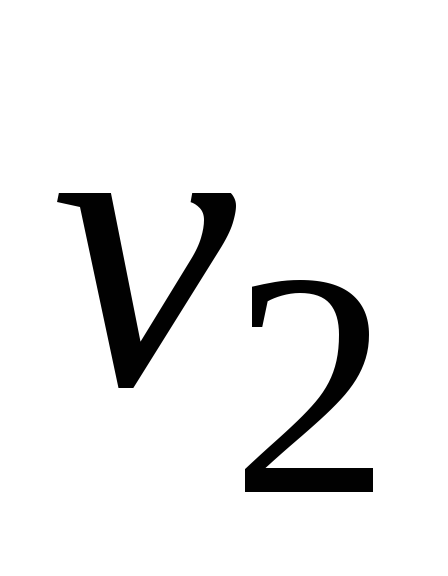 = 1 см/с?
Какой путь
= 1 см/с?
Какой путь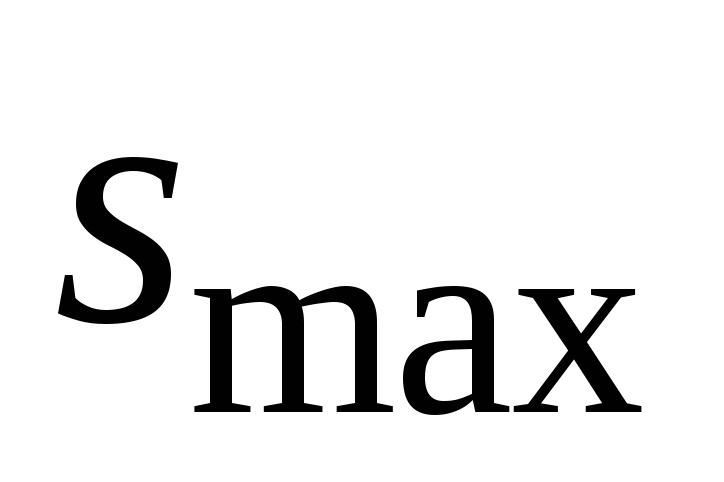 может пройти лодка до полной остановки?
может пройти лодка до полной остановки?В сосуде объемом
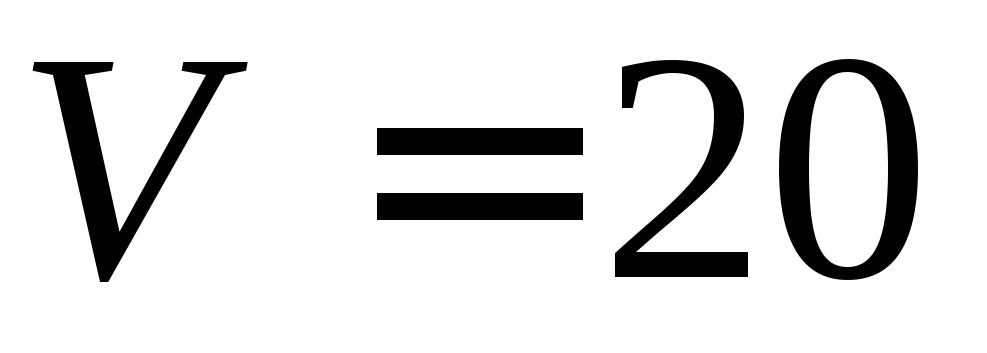 л
в начальный момент содержался воздух
с объёмной долей азота
л
в начальный момент содержался воздух
с объёмной долей азота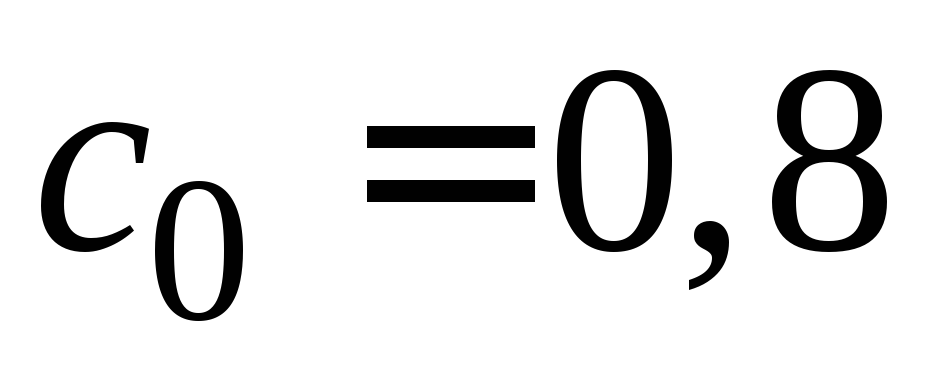 .
В течение последующего времени в сосуд
втекало
.
В течение последующего времени в сосуд
втекало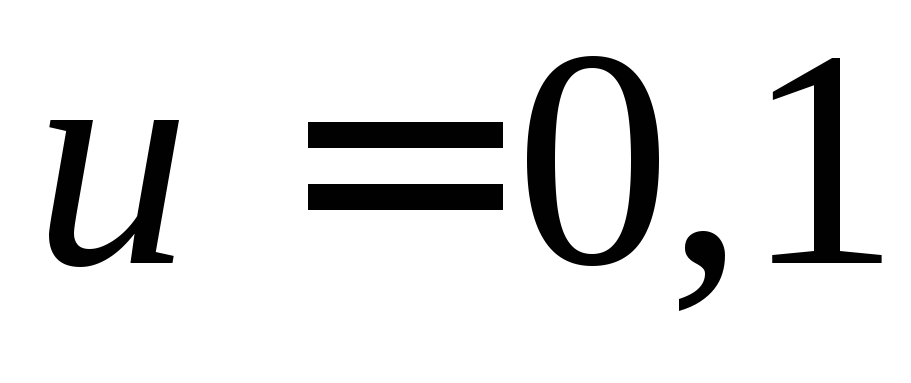 л
азота за секунду, который непрерывно
перемешивался, и вытекало такое же
количество смеси. Найти зависимость
объёмной доли
л
азота за секунду, который непрерывно
перемешивался, и вытекало такое же
количество смеси. Найти зависимость
объёмной доли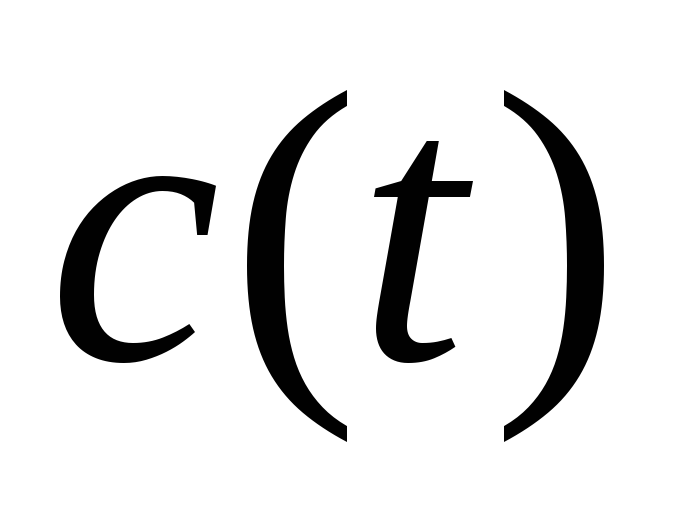 азота в сосуде от времени. Через какое
время
азота в сосуде от времени. Через какое
время объёмная
доля азота в сосуде стала равной
объёмная
доля азота в сосуде стала равной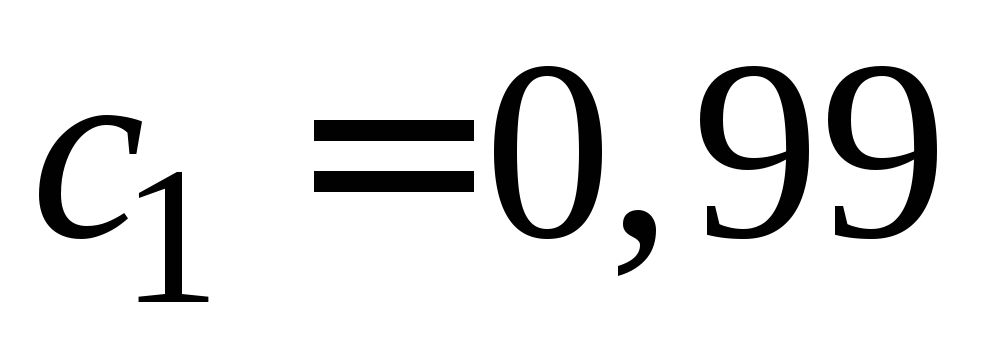 ?
?В баке в начальный момент находилось
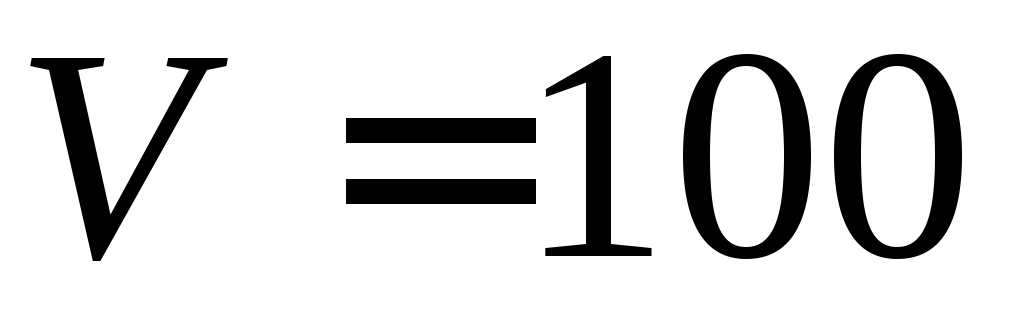 л
раствора, содержащего
л
раствора, содержащего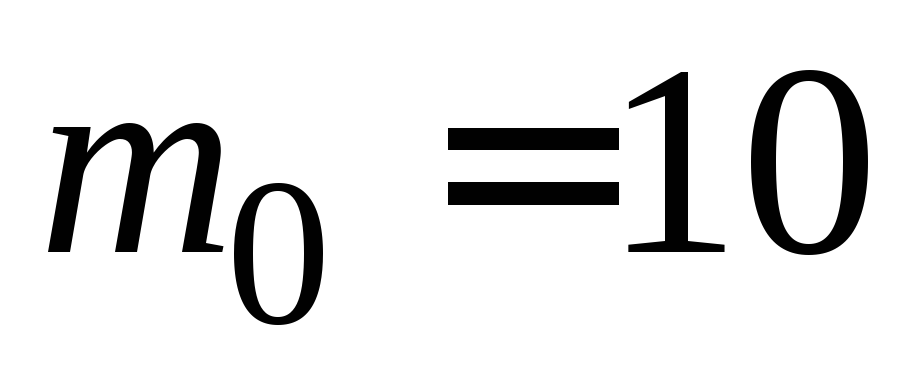 кг
соли. В течение последующего времени
в бак непрерывно подавалась вода со
скоростью
кг
соли. В течение последующего времени
в бак непрерывно подавалась вода со
скоростью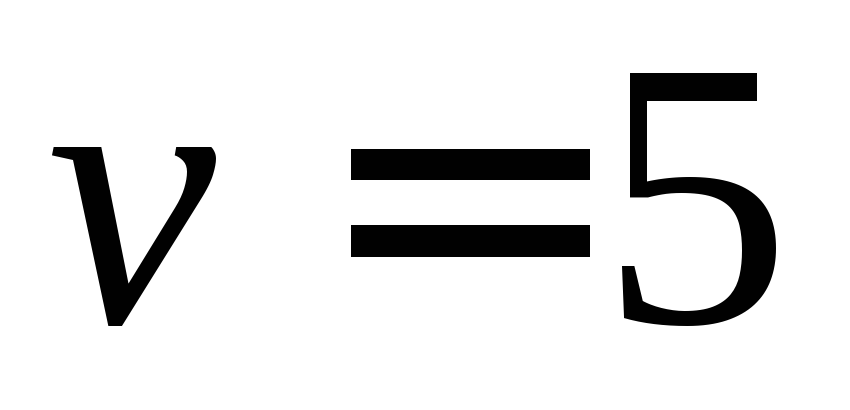 л/мин,
которая перемешивалась с имеющимся
раствором, при этом смесь вытекала с
той же скоростью. Найти зависимость
массы соли
л/мин,
которая перемешивалась с имеющимся
раствором, при этом смесь вытекала с
той же скоростью. Найти зависимость
массы соли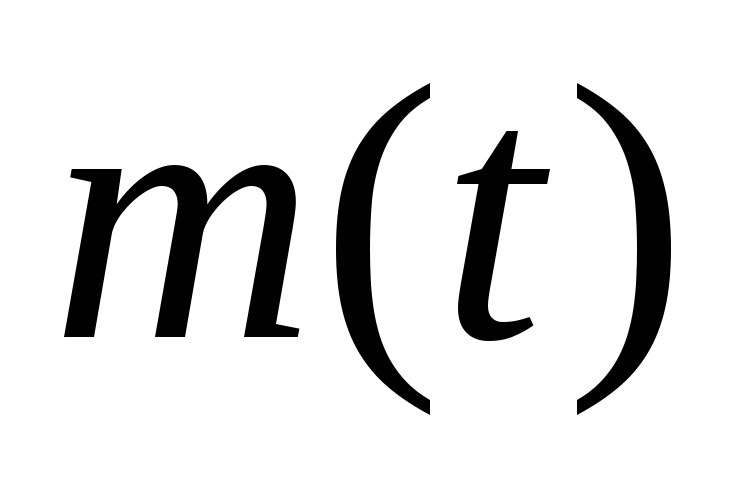 в баке от времени. Какая масса соли
в баке от времени. Какая масса соли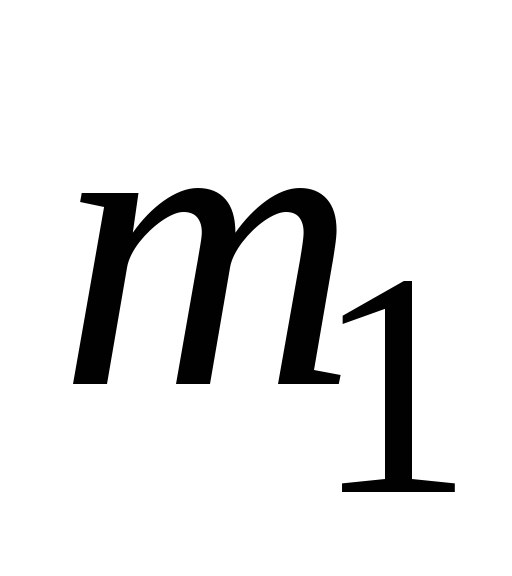 оставалась в баке через
оставалась в баке через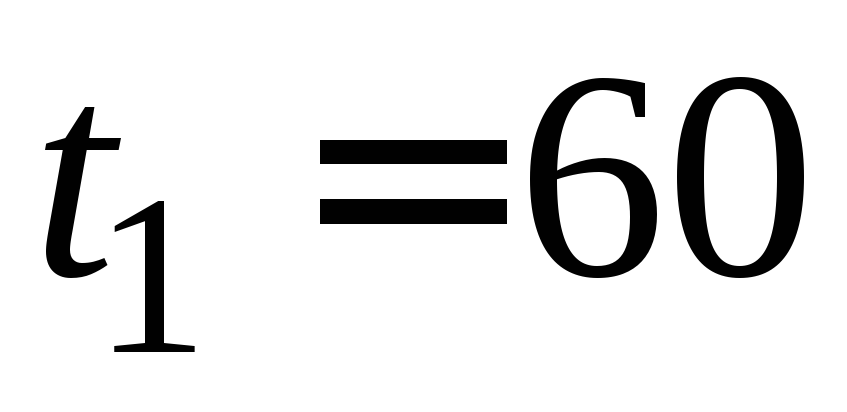 мин?
мин?Первоначальная объёмная доля
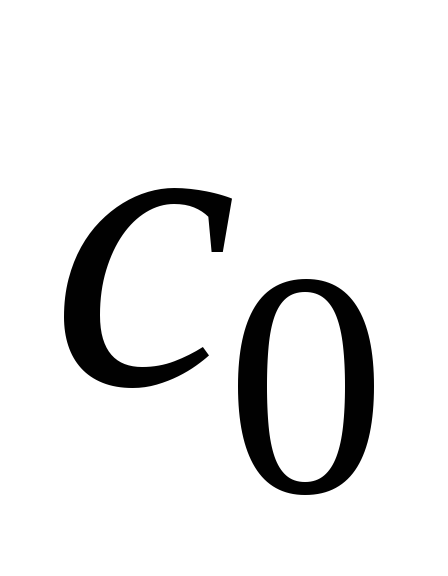 углекислого газа в воздухе комнаты
объемом
углекислого газа в воздухе комнаты
объемом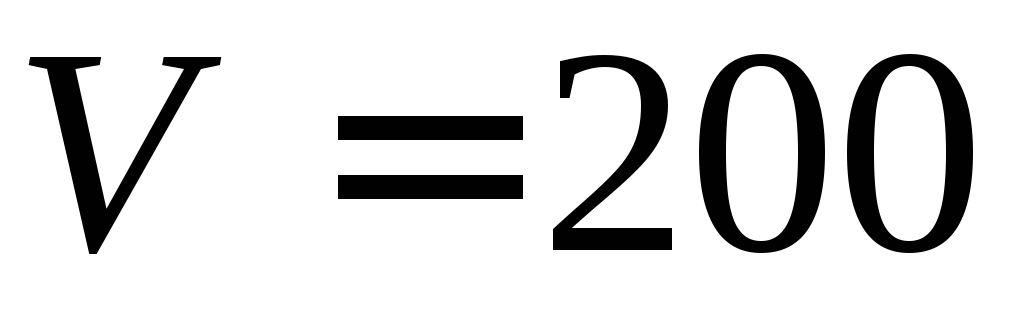 м³
была равна 0,15%. В последующее время
вентиляция подавала в минуту
м³
была равна 0,15%. В последующее время
вентиляция подавала в минуту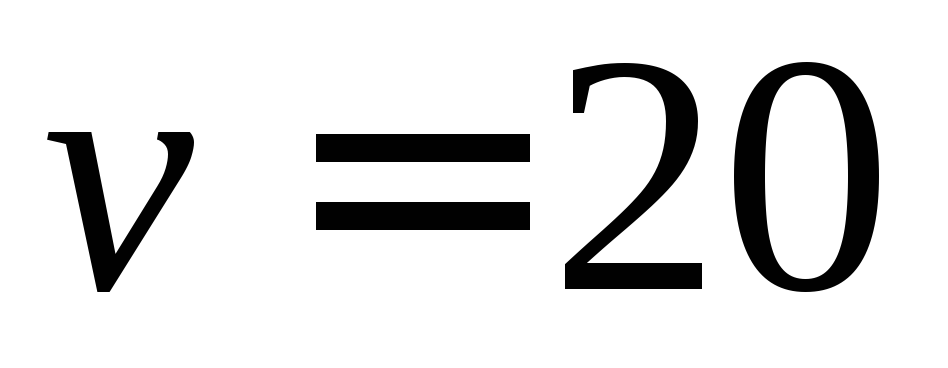 м3воздуха с объёмной долей
м3воздуха с объёмной долей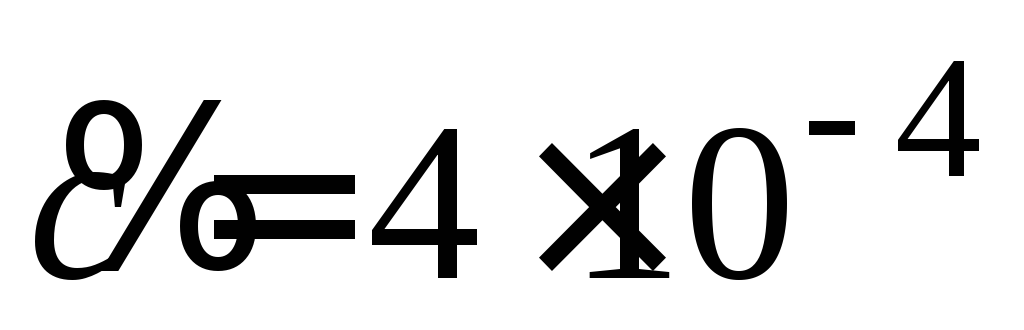 углекислого газа. Найти зависимость
объёмной доли
углекислого газа. Найти зависимость
объёмной доли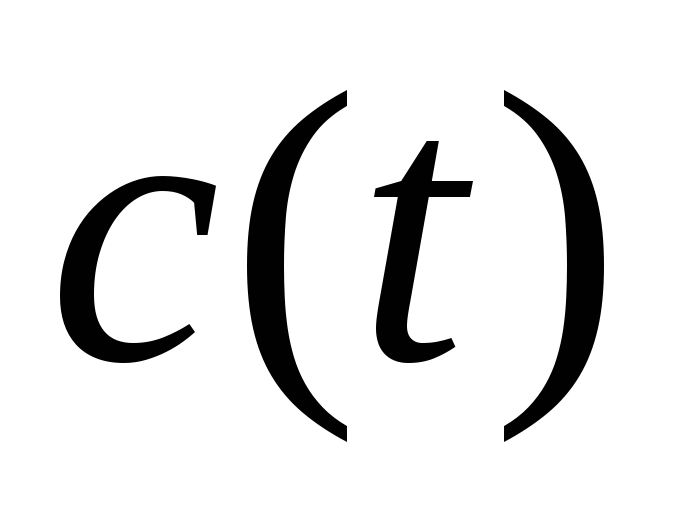 углекислого газа в воздухе комнаты
от времени. Через какое время
углекислого газа в воздухе комнаты
от времени. Через какое время количество углекислого газа в воздухе
комнаты уменьшилось втрое?
количество углекислого газа в воздухе
комнаты уменьшилось втрое?Тело охладилось за
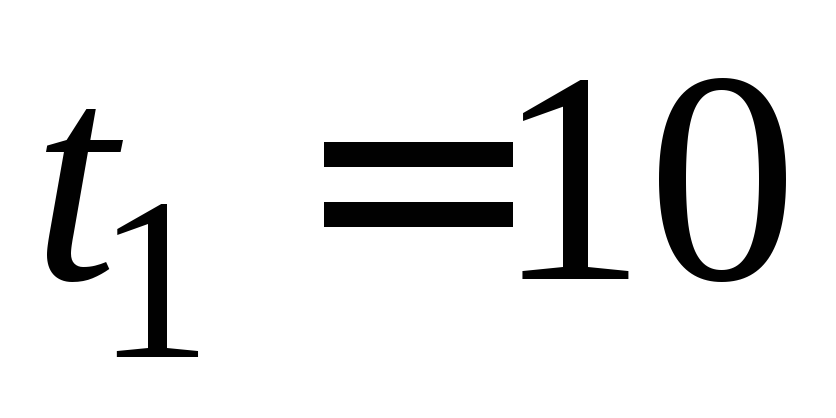 мин от
мин от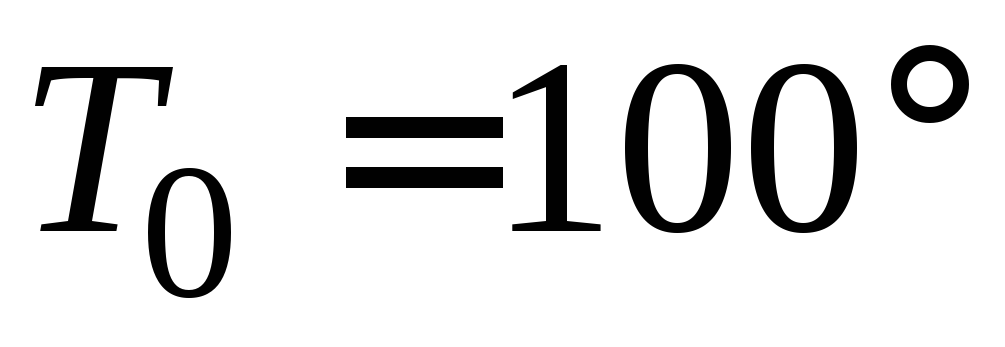 С
до
С
до С.
Температура окружающего воздуха
поддерживается равной
С.
Температура окружающего воздуха
поддерживается равной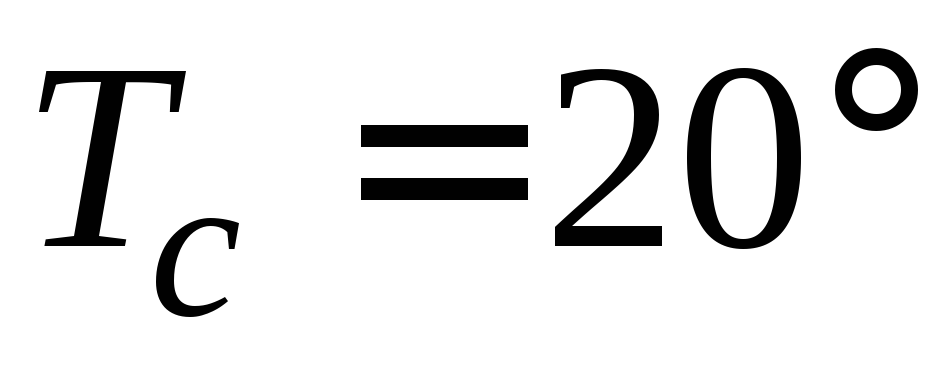 С.
Найти зависимость температуры тела
С.
Найти зависимость температуры тела от времени. К какому моменту времени
от времени. К какому моменту времени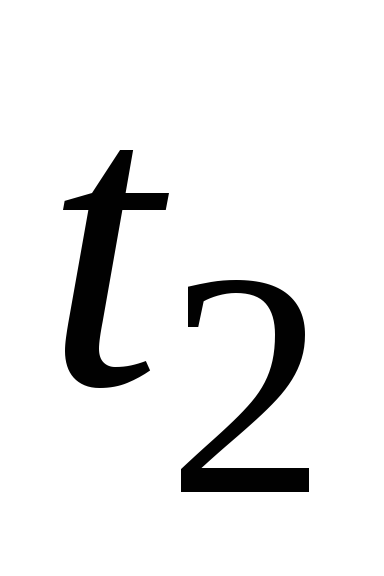 тело остынет до
тело остынет до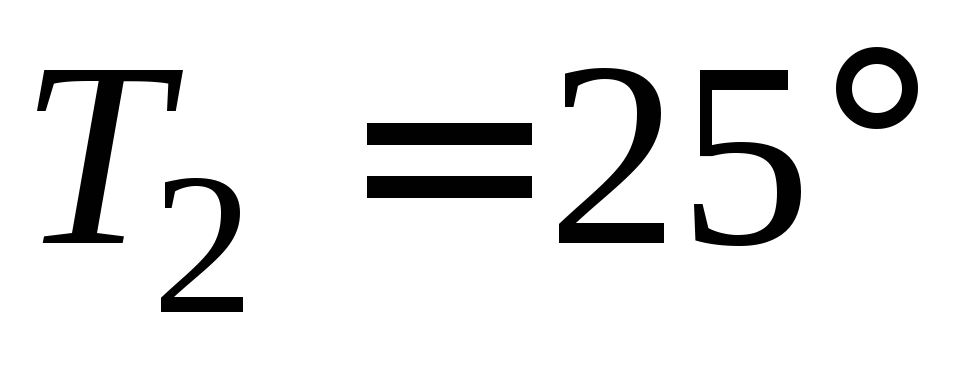 С?
С?Кусок метала с температурой
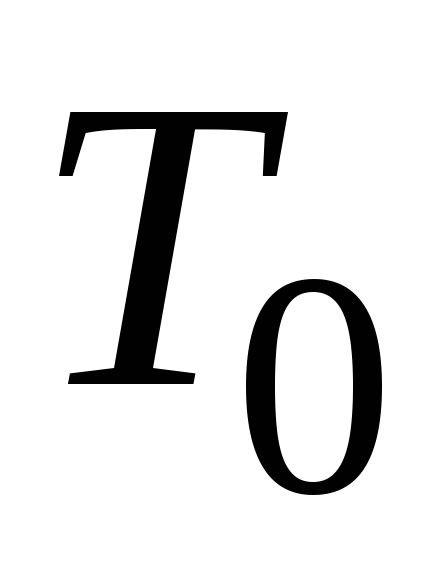 градусов помещен в печь, температура
которой в течение часа равномерно
повышается от
градусов помещен в печь, температура
которой в течение часа равномерно
повышается от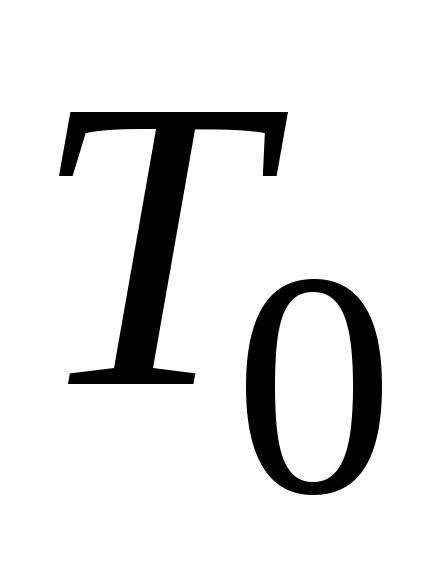 до
до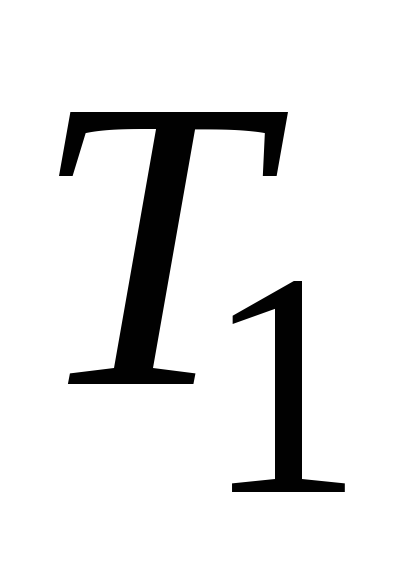 градусов. При разности температур
печи и металла, равной
градусов. При разности температур
печи и металла, равной градусов, металл нагревается со
скоростью
градусов, металл нагревается со
скоростью градусов в минуту. Найти зависимость
температуры металла от времени. Найти
температуру
градусов в минуту. Найти зависимость
температуры металла от времени. Найти
температуру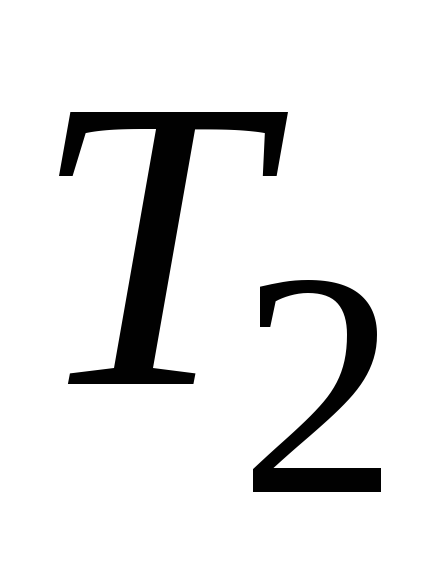 металла через 1 час.
металла через 1 час.За первый день распалось 50% первоначального количества радиоактивного вещества. Найти зависимость количества нераспавшегося радиоактивного вещества
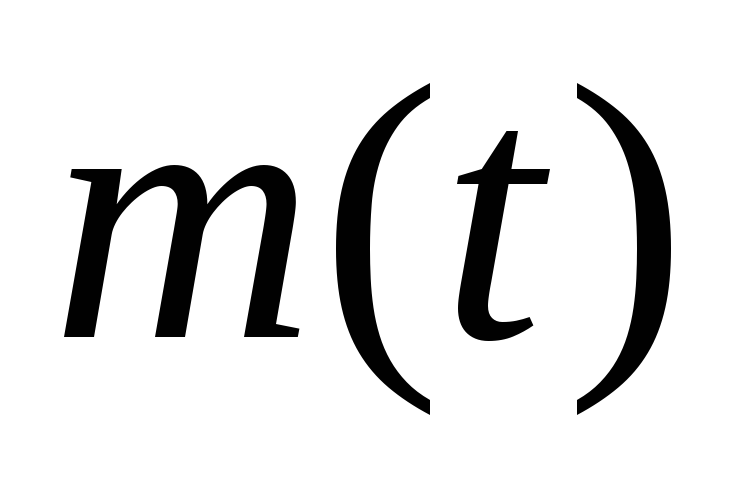 от времени, если вначале оно было равно
от времени, если вначале оно было равно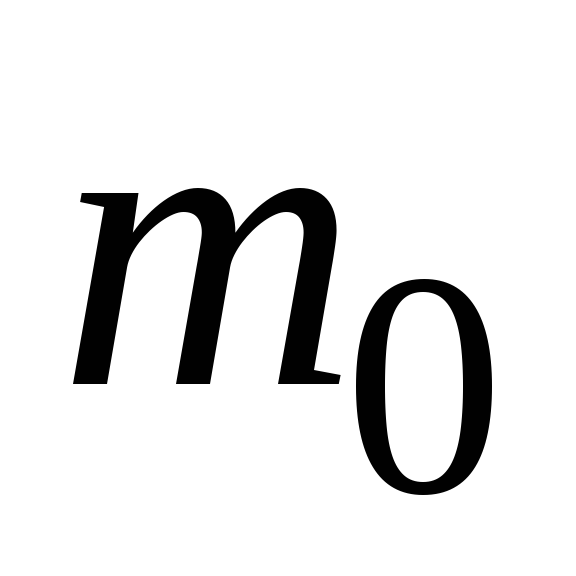 .
Через какой промежуток времени
.
Через какой промежуток времени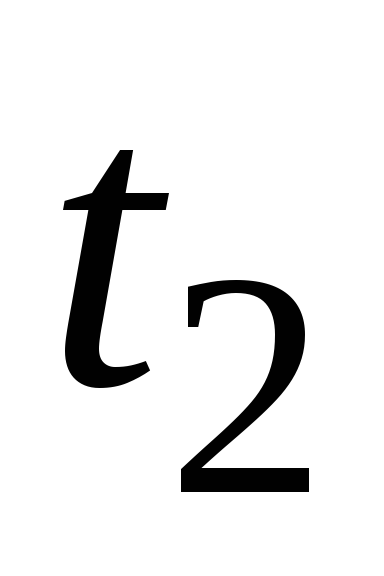 останется 1% от первоначального
количества?
останется 1% от первоначального
количества?Количество света, поглощаемое слоем воды малой толщины, пропорционально количеству падающего на него света и толщине слоя. Слой воды толщиной
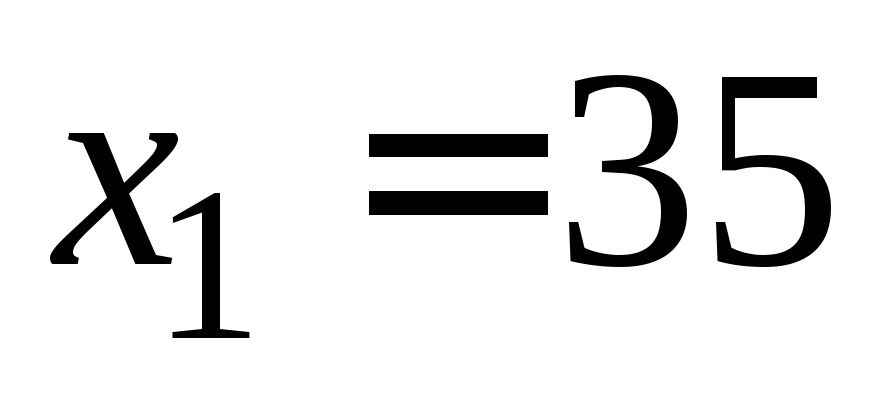 см
поглощает половину падающего на него
света. Найти зависимость количества
(интенсивности) света
см
поглощает половину падающего на него
света. Найти зависимость количества
(интенсивности) света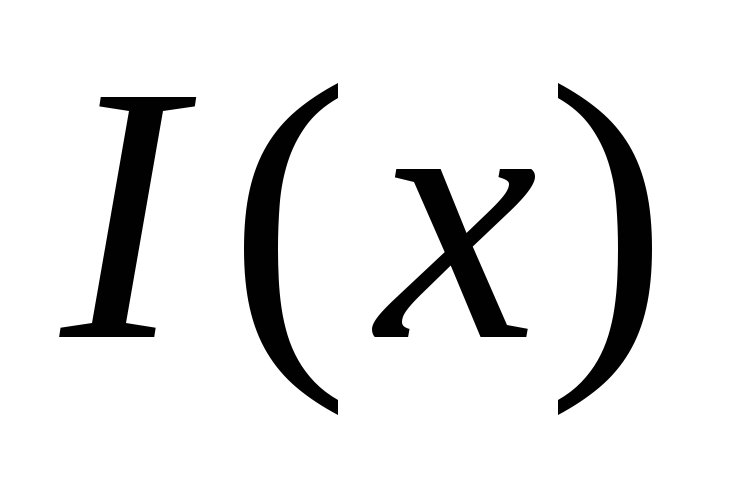 ,
прошедшего сквозь слой воды, от толщины
,
прошедшего сквозь слой воды, от толщины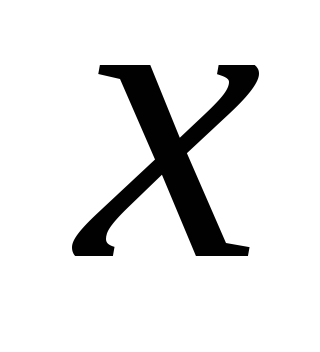 этого слоя, если на слой воды падает
свет интенсивности
этого слоя, если на слой воды падает
свет интенсивности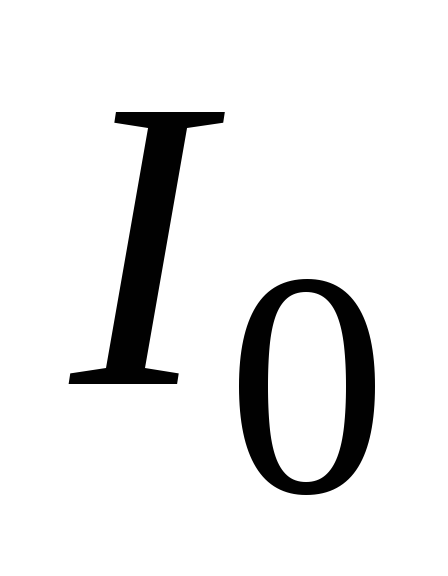 .
Какую часть
.
Какую часть света поглотит слой толщиной в
света поглотит слой толщиной в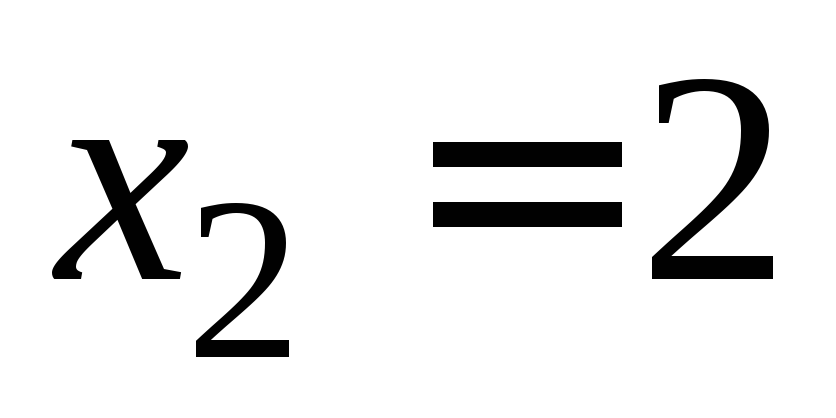 м?
м?Парашютист, совершая затяжной прыжок, раскрыл парашют в момент, когда его скорость
 составляла половину от предельной
скорости
составляла половину от предельной
скорости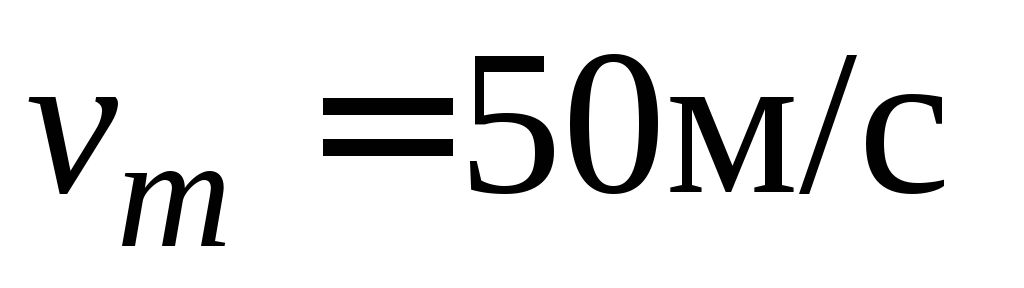 падения человека в воздухе нормальной
плотности. Найти зависимость скорости
парашютиста от времени с начала прыжка,
считая, что сопротивление воздуха
пропорционально квадрату скорости.
В какой момент
падения человека в воздухе нормальной
плотности. Найти зависимость скорости
парашютиста от времени с начала прыжка,
считая, что сопротивление воздуха
пропорционально квадрату скорости.
В какой момент времени от начала прыжка он раскрыл
парашют?
времени от начала прыжка он раскрыл
парашют?Футбольный мяч массой
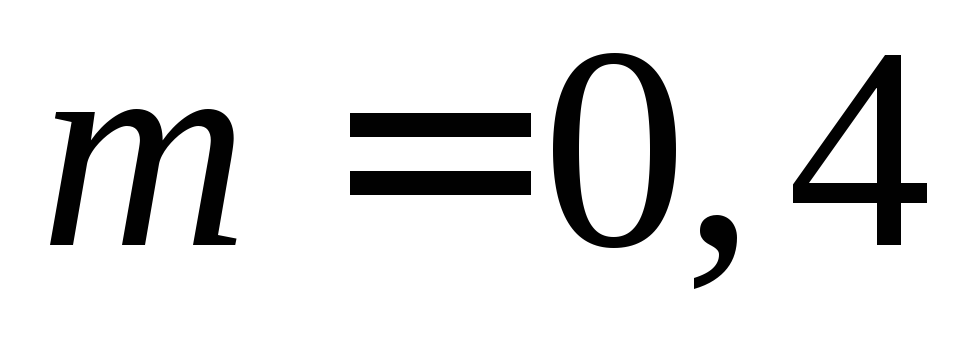 кг
брошен вверх со скоростью
кг
брошен вверх со скоростью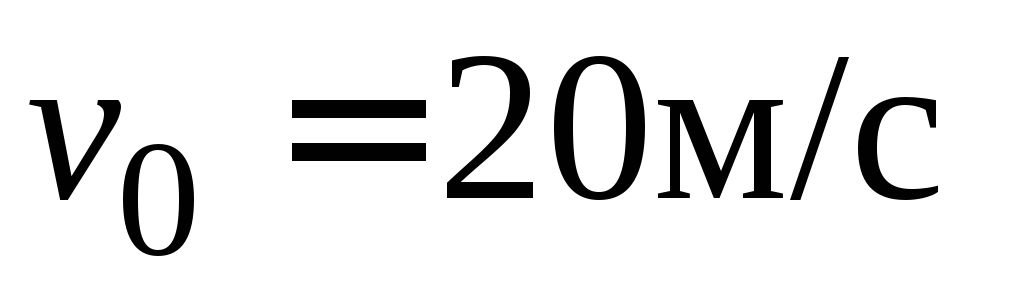 .
Сопротивление воздуха пропорционально
квадрату скорости с коэффициентом
.
Сопротивление воздуха пропорционально
квадрату скорости с коэффициентом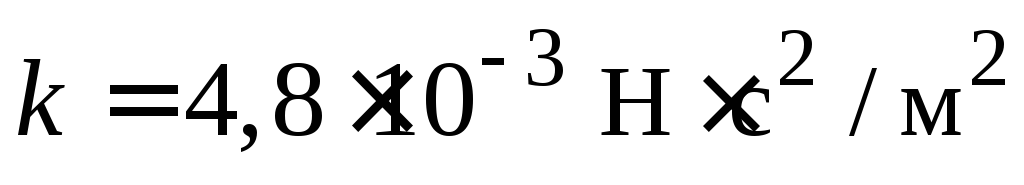 .
Найти зависимость
.
Найти зависимость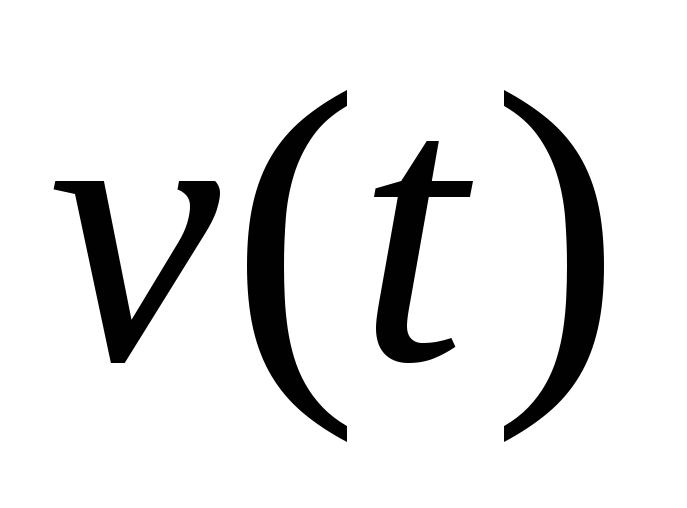 скорости
мяча от времени. Вычислить время
скорости
мяча от времени. Вычислить время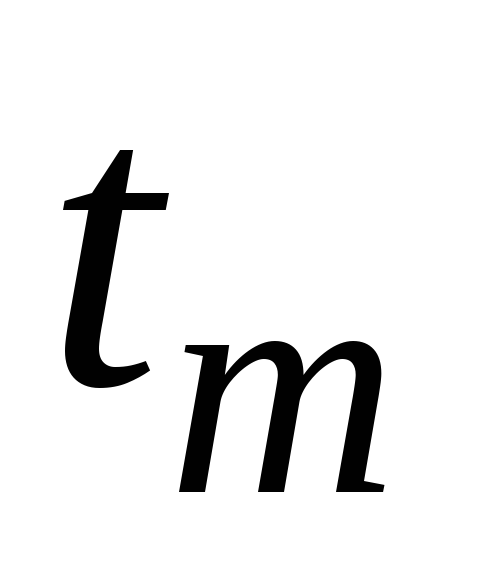 подъёма мяча на наибольшую высоту.
подъёма мяча на наибольшую высоту.Футбольный мяч массой
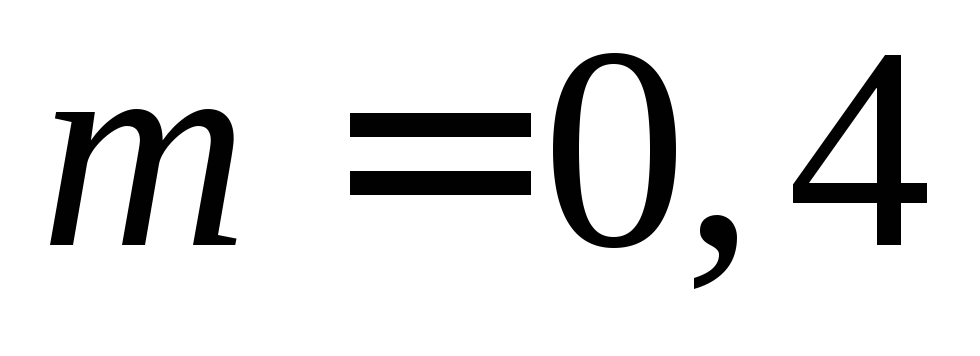 кг
падает с некоторой высоты без начальной
скорости. Найти зависимость скорости
мяча от времени падения, считая, что
сопротивление воздуха пропорционально
скорости мяча с коэффициентом
кг
падает с некоторой высоты без начальной
скорости. Найти зависимость скорости
мяча от времени падения, считая, что
сопротивление воздуха пропорционально
скорости мяча с коэффициентом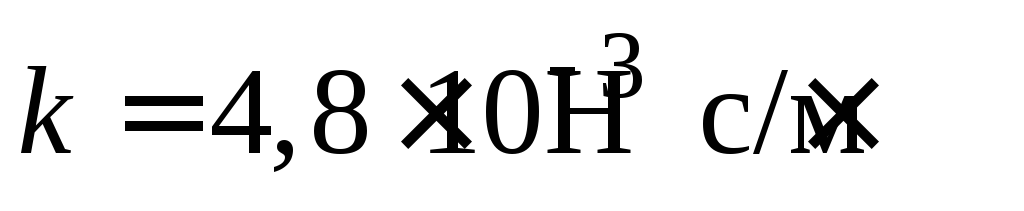 .
Вычислить скорость
.
Вычислить скорость мяча после
мяча после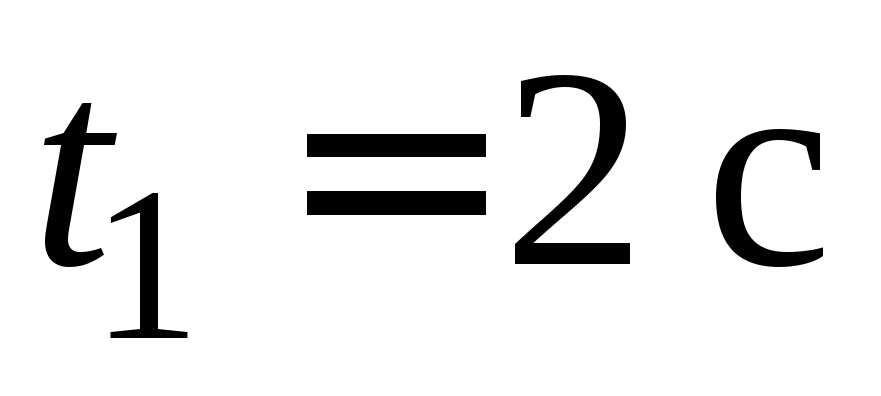 падения.
падения.Из наполненного изначально доверху цилиндрического бака с радиусом
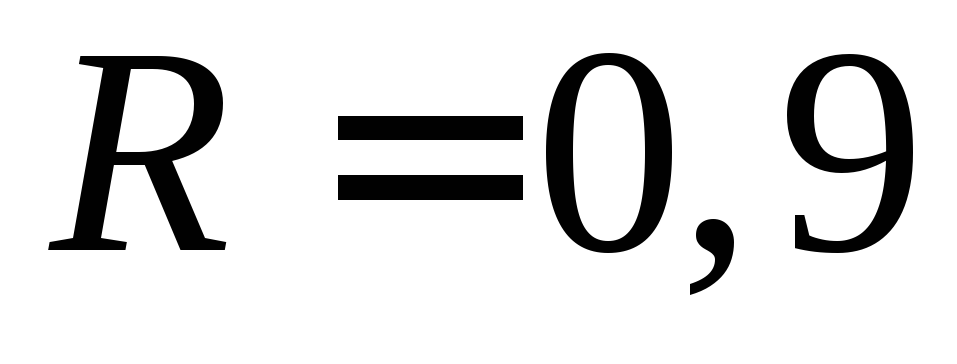 м
и высотой
м
и высотой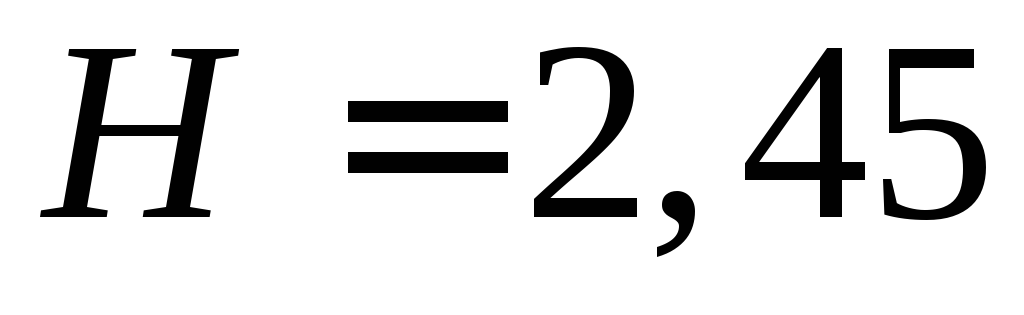 м
через отверстие в дне радиусом
м
через отверстие в дне радиусом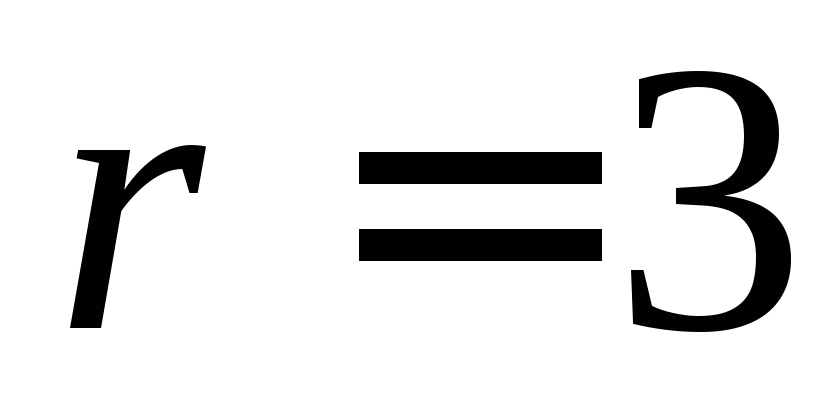 см
вытекает вода. Найти зависимость
см
вытекает вода. Найти зависимость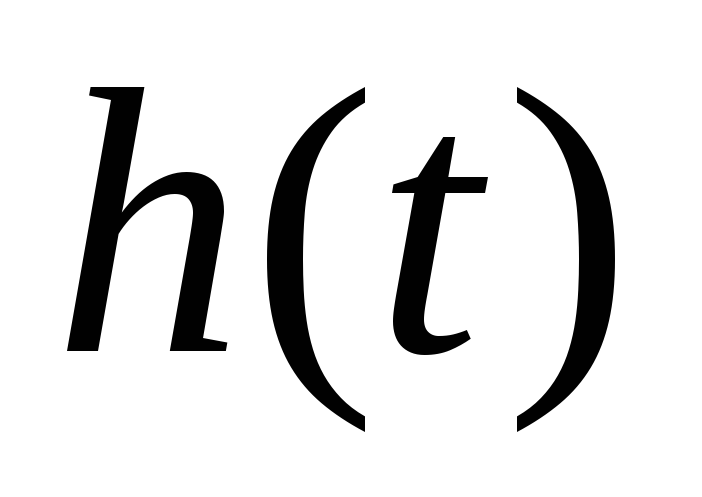 уровня воды в баке от времени. За какой
промежуток
уровня воды в баке от времени. За какой
промежуток времени вытечет вся вода? Ось цилиндра
вертикальна.
времени вытечет вся вода? Ось цилиндра
вертикальна.Из полного цилиндрического бака высотой
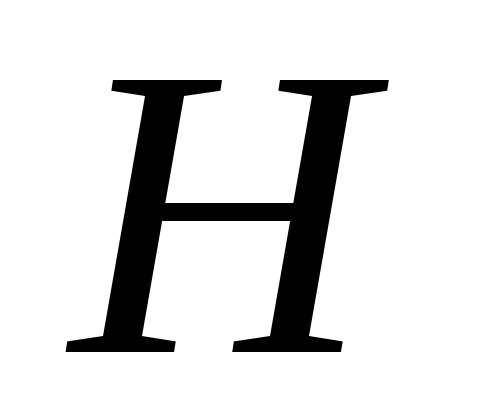 через отверстие в дне половина воды
вытекает за
через отверстие в дне половина воды
вытекает за =5 мин.
Найти зависимость
=5 мин.
Найти зависимость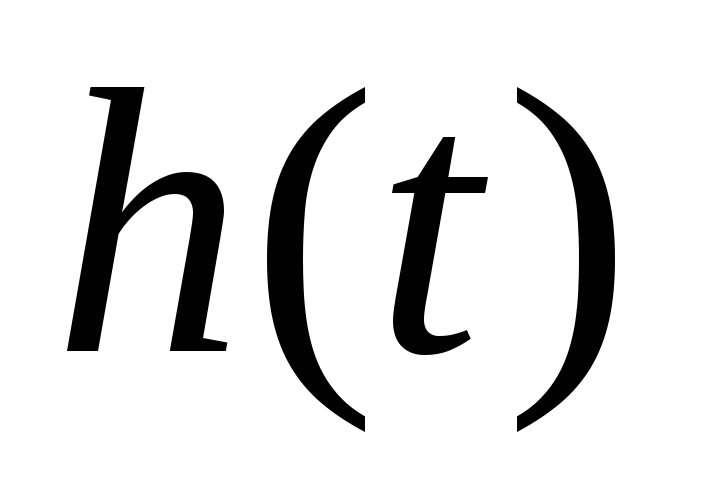 уровня воды в баке от времени. За какой
промежуток
уровня воды в баке от времени. За какой
промежуток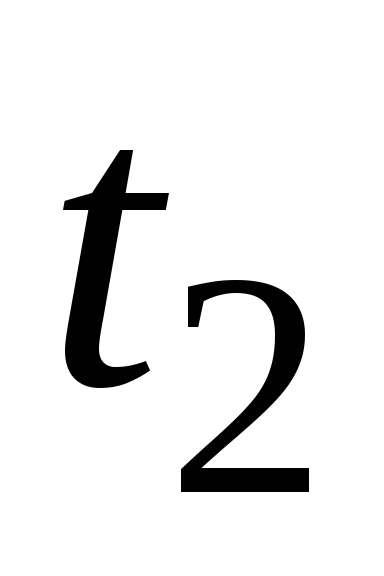 времени вытечет вся вода? Ось цилиндра
вертикальна.
времени вытечет вся вода? Ось цилиндра
вертикальна.В прямоугольный бак длиной
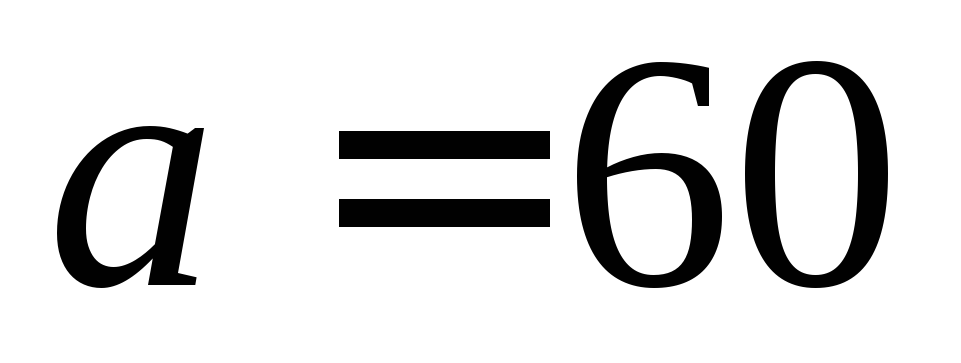 см,
шириной
см,
шириной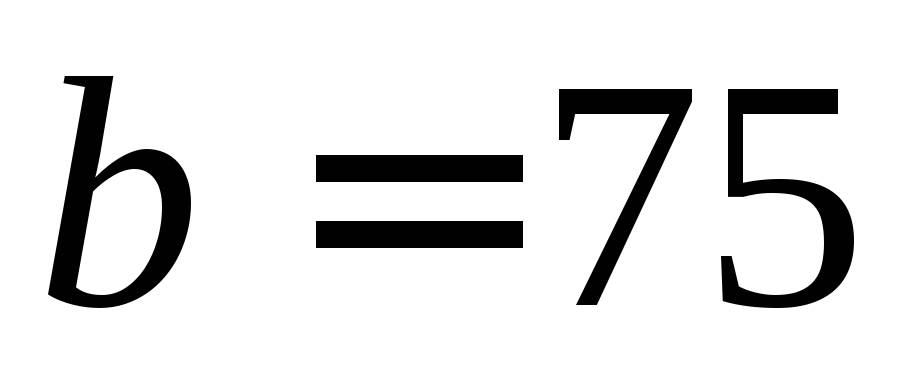 см
и высотой
см
и высотой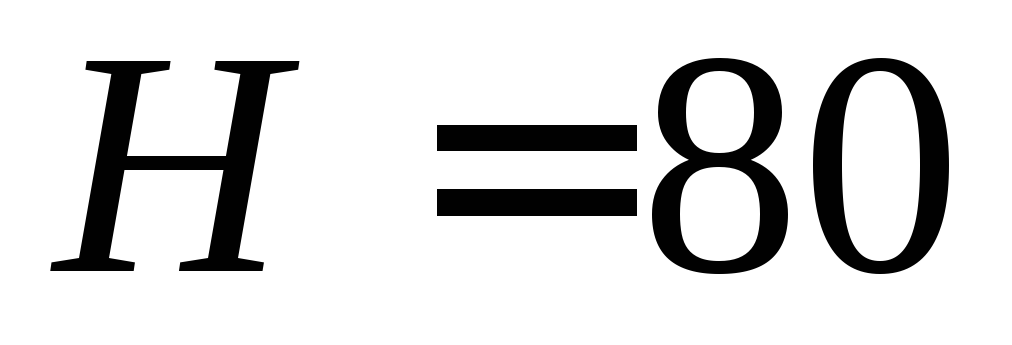 см
поступает вода со скоростью
см
поступает вода со скоростью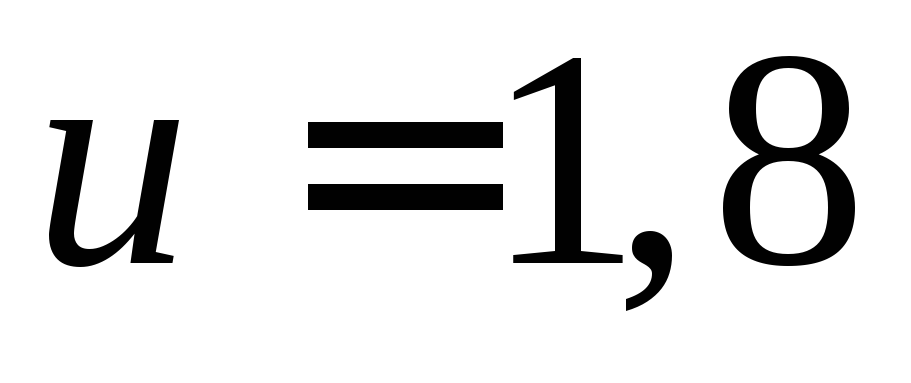 л/с.
В дне имеется отверстие площадью
л/с.
В дне имеется отверстие площадью см².
Найти зависимость между временем
наполнения бака и уровнем воды
см².
Найти зависимость между временем
наполнения бака и уровнем воды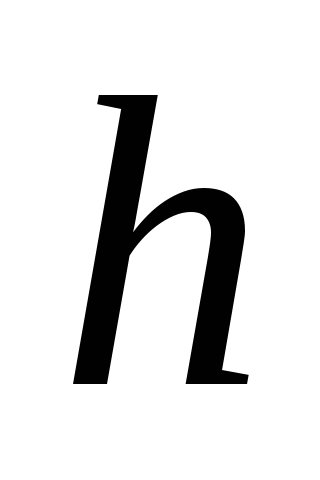 в нём. За какое время
в нём. За какое время наполняется весь бак?
наполняется весь бак?В начальный момент воронка в форме конуса радиусом
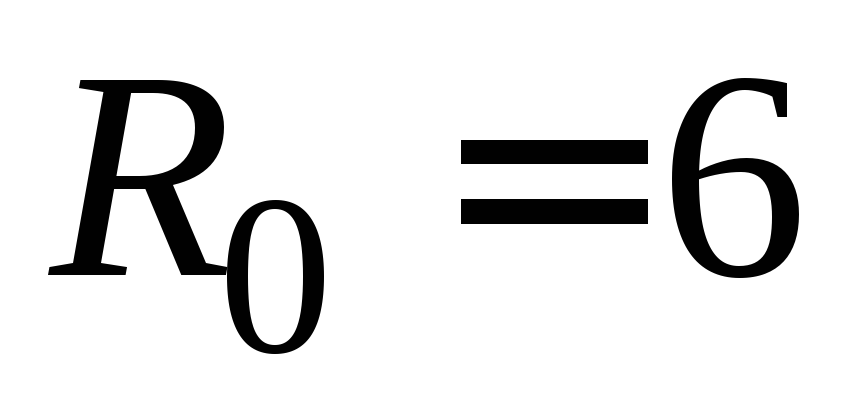 см
и высотой
см
и высотой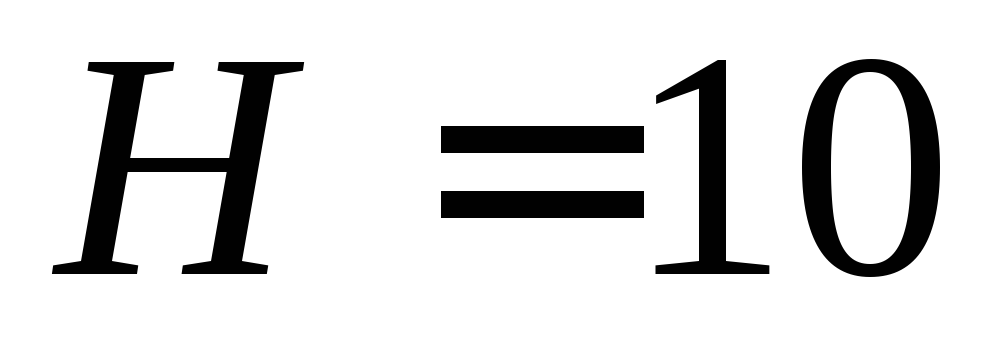 см,
обращенного вершиной вниз, доверху
наполнена водой. В вершине конуса
имеется отверстие радиусом
см,
обращенного вершиной вниз, доверху
наполнена водой. В вершине конуса
имеется отверстие радиусом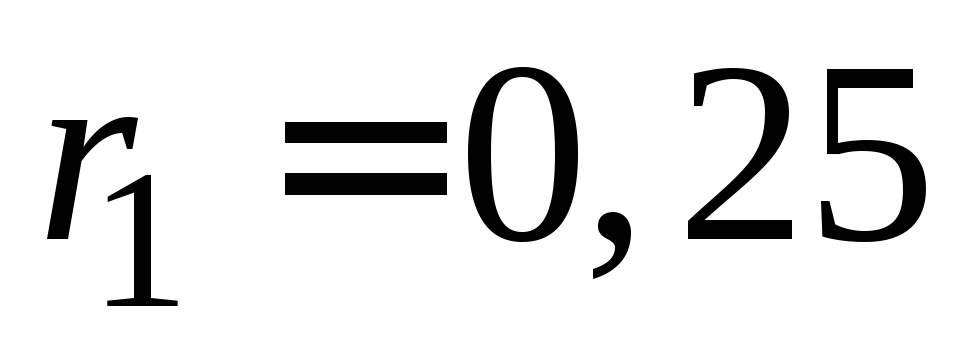 см,
через которое вытекает вода. Найти
зависимость между временем, прошедшим
с начального момента, и уровнем воды
см,
через которое вытекает вода. Найти
зависимость между временем, прошедшим
с начального момента, и уровнем воды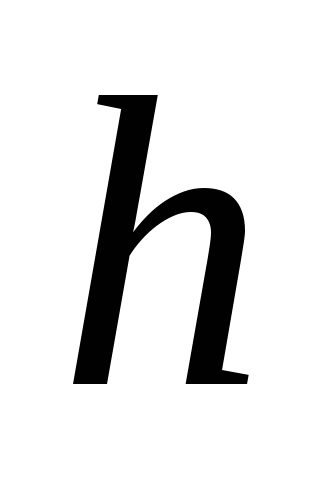 в воронке. За какое время
в воронке. За какое время из воронки вытечет вся вода?
из воронки вытечет вся вода?В начальный момент бак в форме конуса радиусом
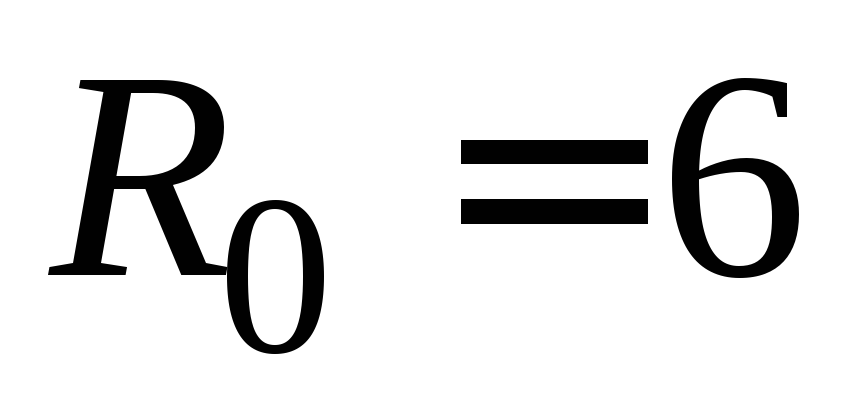 см
и высотой
см
и высотой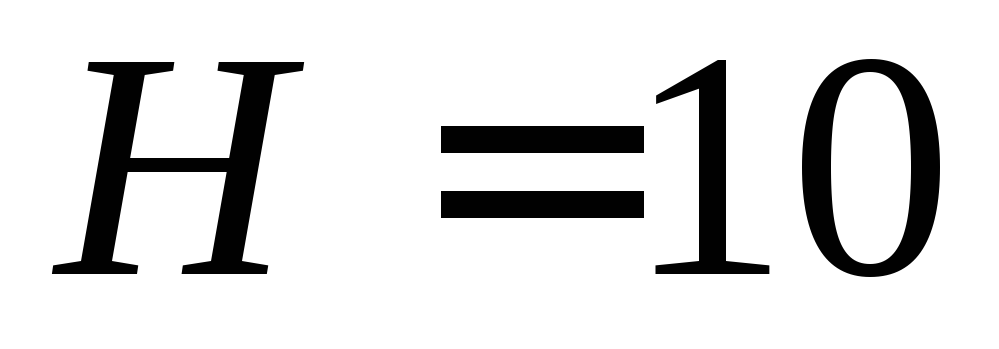 см
вершиной вверх заполнен водой. В
основании конуса имеется отверстие
радиусом
см
вершиной вверх заполнен водой. В
основании конуса имеется отверстие
радиусом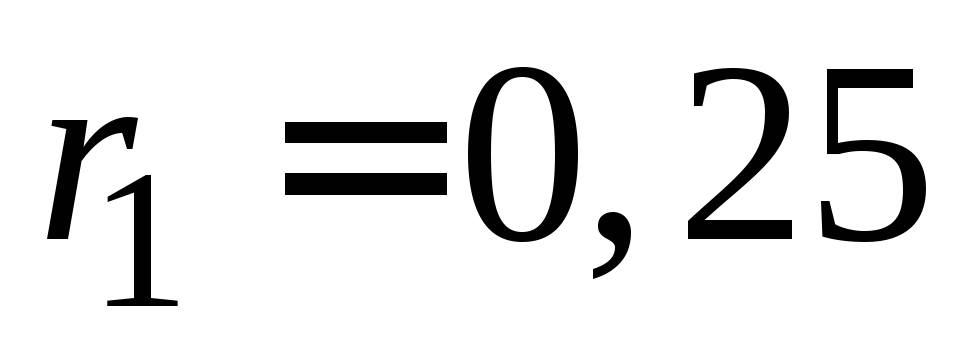 см,
через которое вытекает вода. Найти
зависимость между временем, прошедшим
с начального момента, и уровнем воды
см,
через которое вытекает вода. Найти
зависимость между временем, прошедшим
с начального момента, и уровнем воды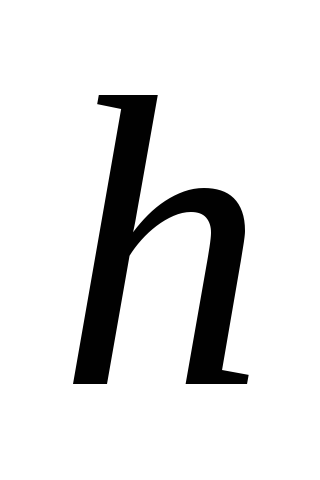 в баке. За какое время
в баке. За какое время из бака вытечет вся вода?
из бака вытечет вся вода?Бак имеет форму клина ребром вниз, торцевые стенки которого перпендикулярны боковым. Длина клина равна
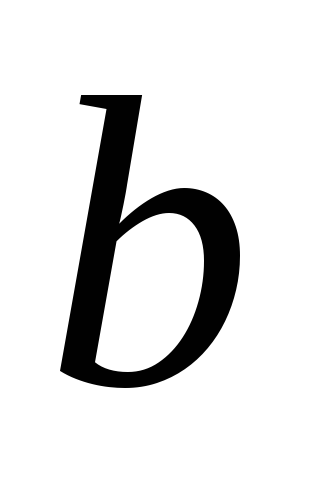 ,
высота
,
высота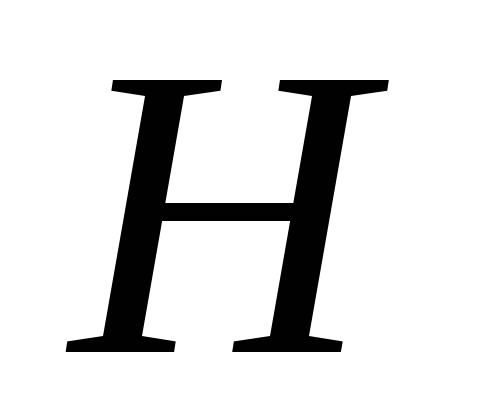 ,
длина основания торца равна
,
длина основания торца равна ,
в нижнем ребре клина сделано отверстие
площадью
,
в нижнем ребре клина сделано отверстие
площадью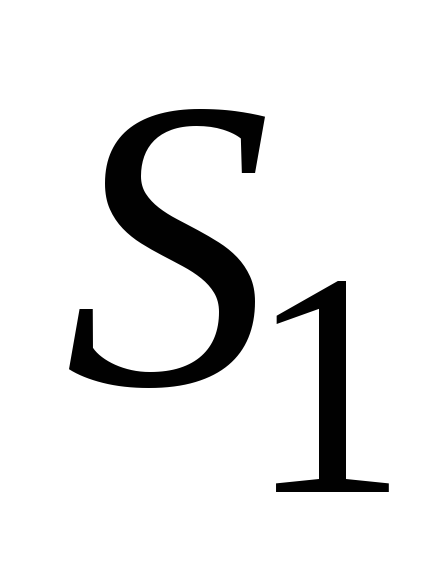 ,
через которое может вытекать вода. В
начальный момент бак заполнен водой.
Найти зависимость между временем,
прошедшим с начального момента, и
уровнем воды
,
через которое может вытекать вода. В
начальный момент бак заполнен водой.
Найти зависимость между временем,
прошедшим с начального момента, и
уровнем воды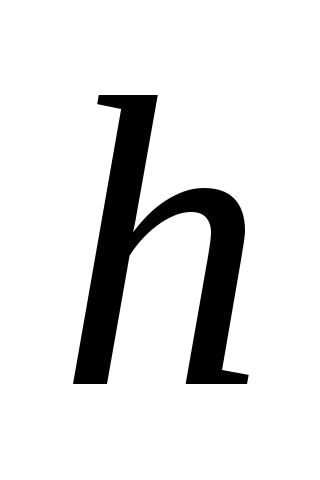 в баке. За какое время
в баке. За какое время из бака вытечет вся вода?
из бака вытечет вся вода?Бак имеет форму клина ребром вверх, торцевые стенки которого перпендикулярны боковым. Длина клина равна
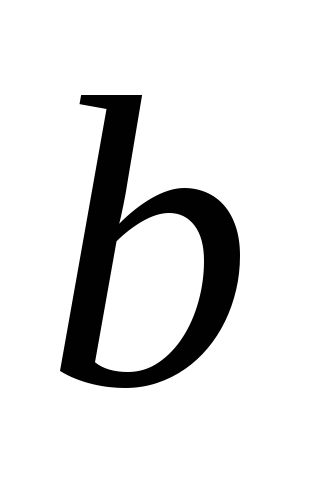 ,
высота –
,
высота –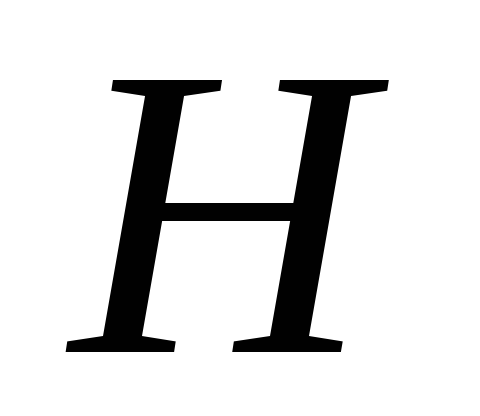 ,
длина основания торца равна
,
длина основания торца равна ,
в нижнем основании бака сделано
отверстие площадью
,
в нижнем основании бака сделано
отверстие площадью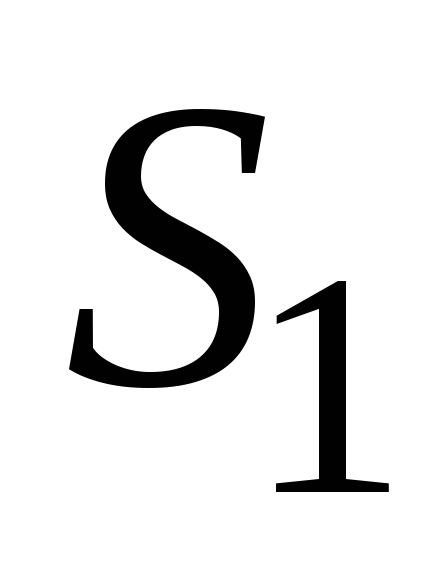 ,
через которое может вытекать вода. В
начальный момент бак заполнен водой.
Найти зависимость между временем,
прошедшим с начального момента, и
уровнем воды
,
через которое может вытекать вода. В
начальный момент бак заполнен водой.
Найти зависимость между временем,
прошедшим с начального момента, и
уровнем воды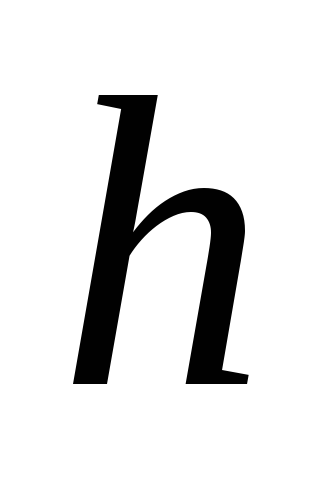 в баке. За какое время
в баке. За какое время из бака вытечет вся вода?
из бака вытечет вся вода?Бак имеет форму шара радиусом
 ,
в самой нижней части бака сделано
отверстие площадью
,
в самой нижней части бака сделано
отверстие площадью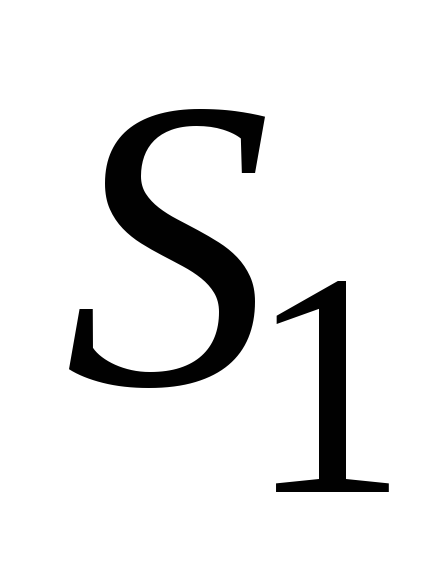 ,
через которое может вытекать вода. В
начальный момент бак заполнен водой.
Найти зависимость между временем,
прошедшим с начального момента, и
уровнем воды
,
через которое может вытекать вода. В
начальный момент бак заполнен водой.
Найти зависимость между временем,
прошедшим с начального момента, и
уровнем воды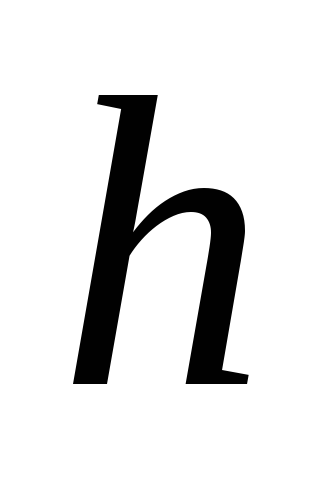 в баке. За какое время
в баке. За какое время из бака вытечет вся вода?
из бака вытечет вся вода?Незаряженный в момент
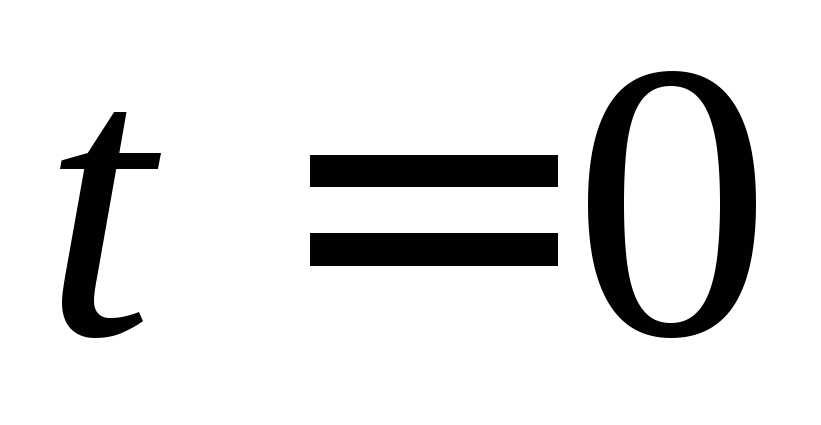 конденсатор ёмкостью
конденсатор ёмкостью последовательно с сопротивлением
последовательно с сопротивлением включается в цепь с источником,
напряжение на котором линейно возрастает
от 0 до
включается в цепь с источником,
напряжение на котором линейно возрастает
от 0 до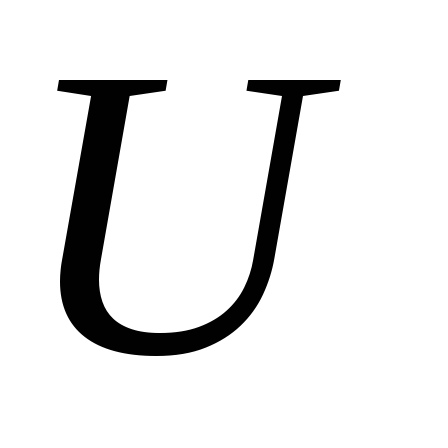 за промежуток времени от
за промежуток времени от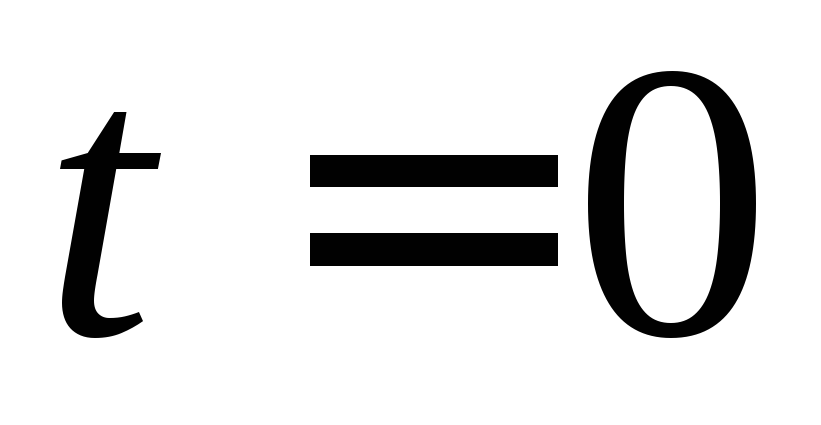 до
до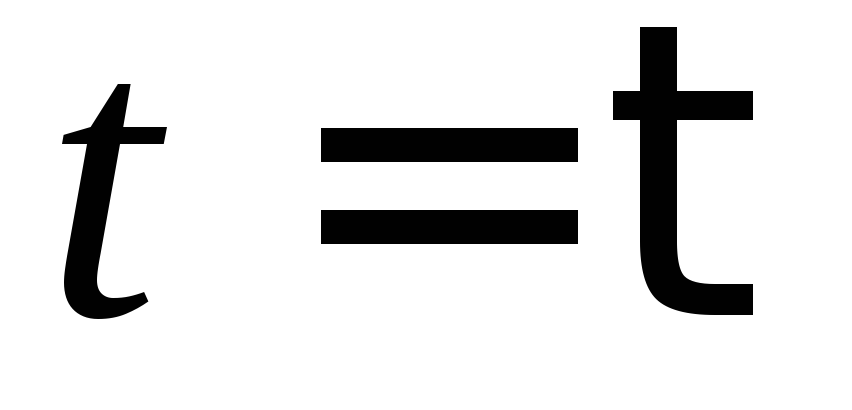 .
Найти заряд
.
Найти заряд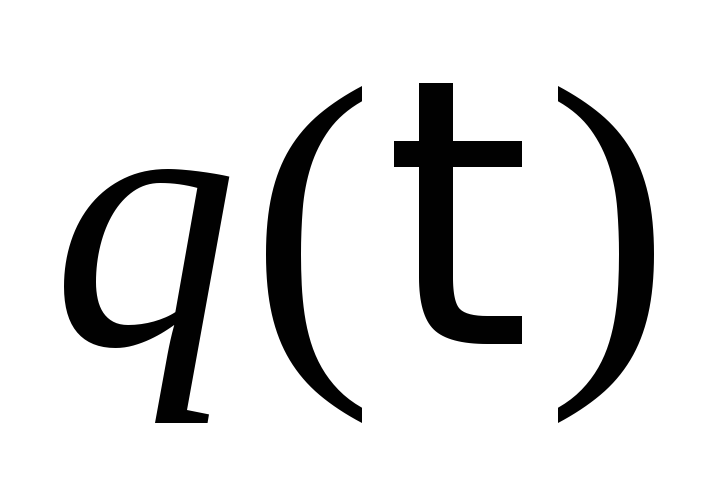 на конденсаторе в момент времени
на конденсаторе в момент времени .
.Катушка с индуктивностью
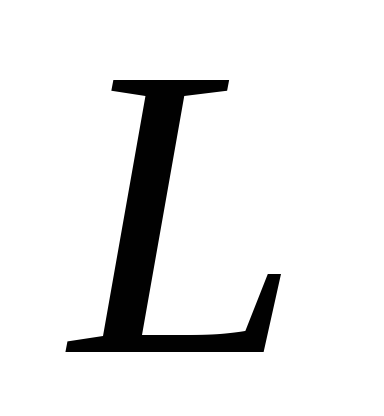 включается последовательно с
сопротивлением
включается последовательно с
сопротивлением в цепь с источником, напряжение на
котором линейно возрастает от 0 до
в цепь с источником, напряжение на
котором линейно возрастает от 0 до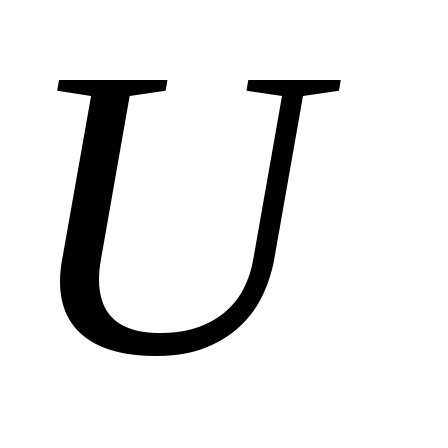 за промежуток времени от
за промежуток времени от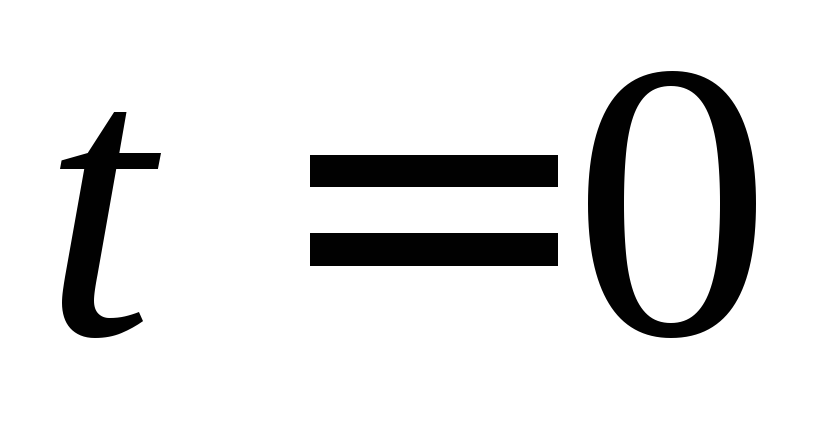 до
до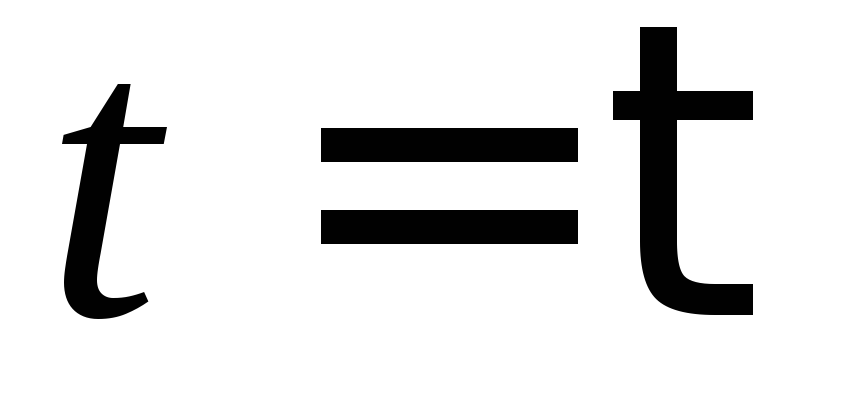 .
В момент замыкания цепи ток в ней равен
нулю. Найти ток
.
В момент замыкания цепи ток в ней равен
нулю. Найти ток в катушке в момент времени
в катушке в момент времени .
.Найти атмосферное давление на высоте
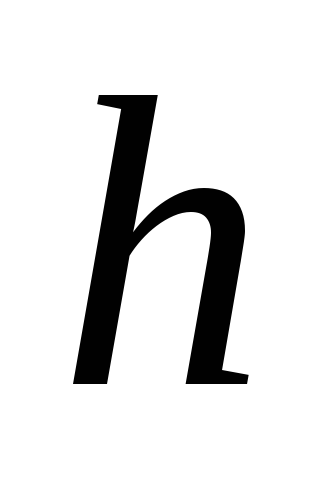 ,
если на поверхности земли давление
равно
,
если на поверхности земли давление
равно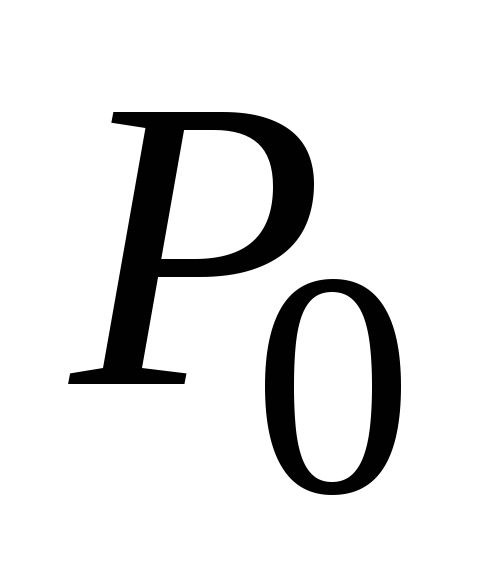 и плотность воздуха
и плотность воздуха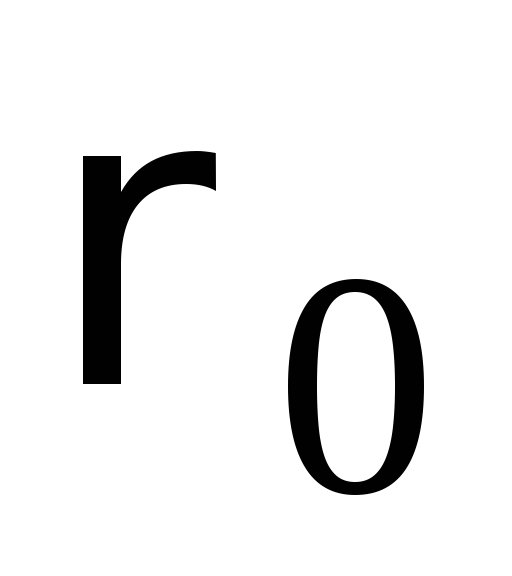 .
Использовать закон Бойля – Мариотта,
в соответствии с которым плотность
пропорциональна давлению (пренебречь
изменением температуры воздуха при
изменении высоты).
.
Использовать закон Бойля – Мариотта,
в соответствии с которым плотность
пропорциональна давлению (пренебречь
изменением температуры воздуха при
изменении высоты).Незаряженный конденсатор ёмкостью
 включается в цепь с напряжением
включается в цепь с напряжением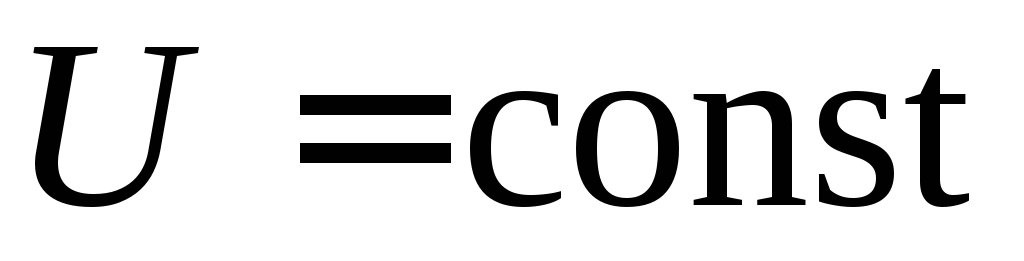 и сопротивлением
и сопротивлением .
Определить заряд
.
Определить заряд на конденсаторе в момент времени
на конденсаторе в момент времени .
.Катушка с индуктивностью
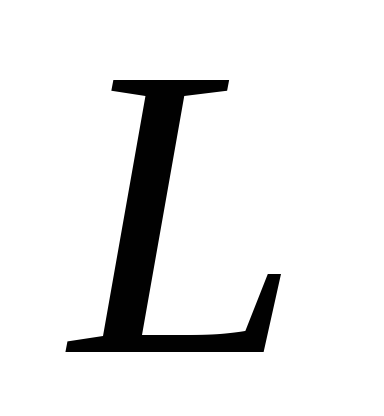 включается последовательно с
сопротивлением
включается последовательно с
сопротивлением в цепь с напряжением
в цепь с напряжением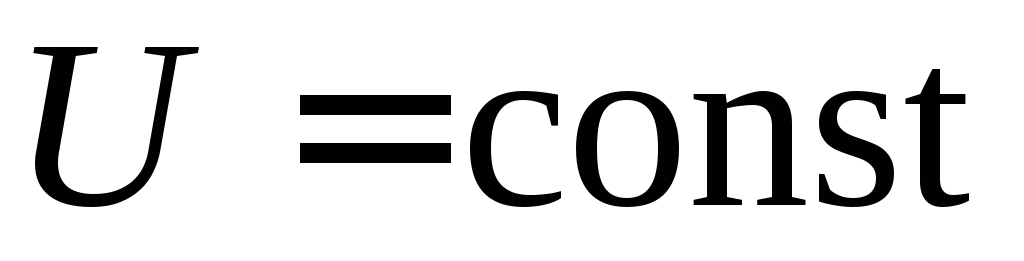 .
В момент замыкания цепи ток в ней равен
нулю. Найти ток
.
В момент замыкания цепи ток в ней равен
нулю. Найти ток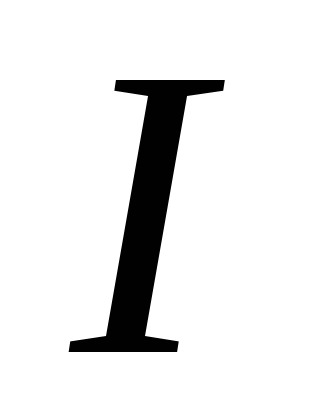 в катушке в момент времени
в катушке в момент времени .
.Напряжение между обкладками плоского конденсатора линейно возрастает за 1 с от
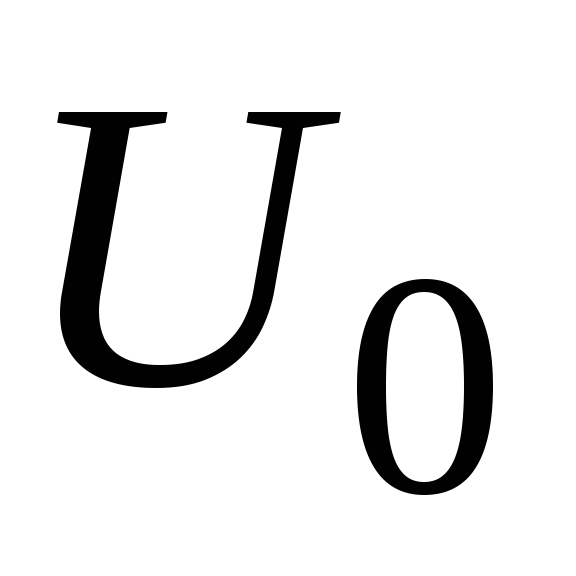 до
до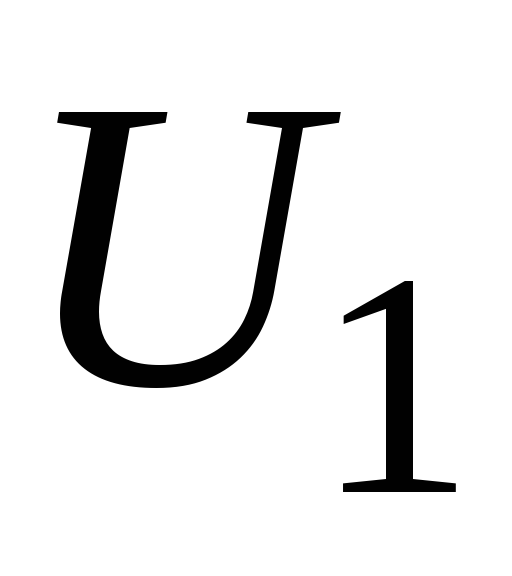 .
В начальный момент от одной из обкладок
отрывается пылинка массой
.
В начальный момент от одной из обкладок
отрывается пылинка массой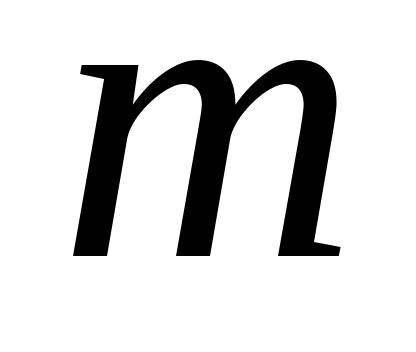 с зарядом
с зарядом и начинает двигаться к другой обкладке,
испытывая сопротивление со стороны
воздуха, заполняющего пространство
между обкладками, которое пропорционально
скорости пылинки с коэффициентом
и начинает двигаться к другой обкладке,
испытывая сопротивление со стороны
воздуха, заполняющего пространство
между обкладками, которое пропорционально
скорости пылинки с коэффициентом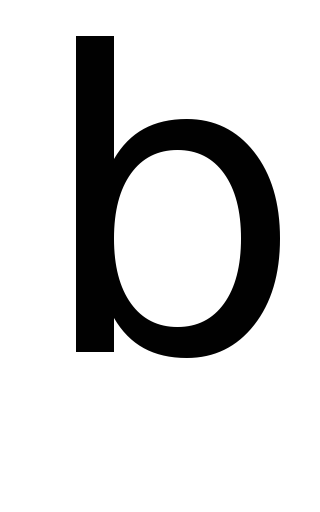 .
Найти зависимость скорости пылинки
от времени. Расстояние между обкладками
равно
.
Найти зависимость скорости пылинки
от времени. Расстояние между обкладками
равно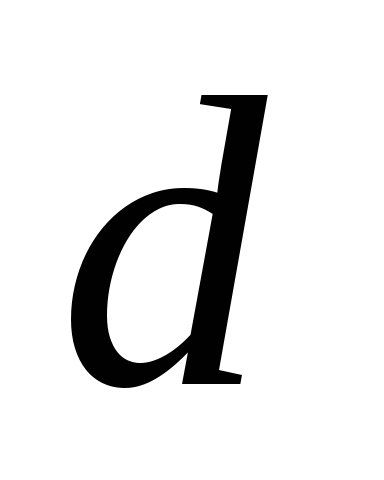 ,
краевыми эффектами и силой тяжести
пренебречь.
,
краевыми эффектами и силой тяжести
пренебречь.Метеорит, находящийся под влиянием земного притяжения, из состояния покоя начинает прямолинейно падать на Землю с высоты
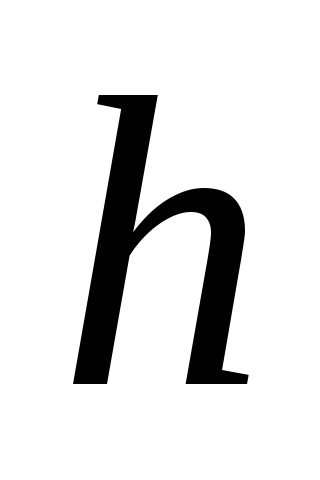 (над поверхностью Земли). Найти
зависимость скорости
(над поверхностью Земли). Найти
зависимость скорости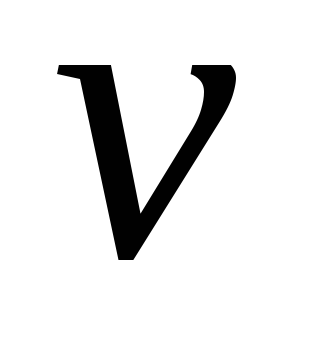 метеорита от расстояния
метеорита от расстояния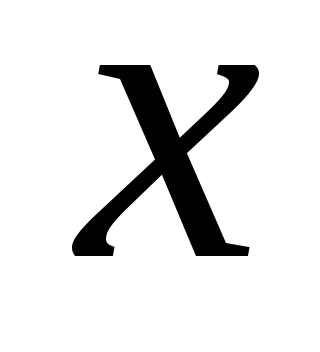 ,
пройденного им, при условии отсутствия
земной атмосферы. Радиус Земли
,
пройденного им, при условии отсутствия
земной атмосферы. Радиус Земли ,
ускорение свободного падения на
поверхности Земли
,
ускорение свободного падения на
поверхности Земли .
.Катушка с индуктивностью
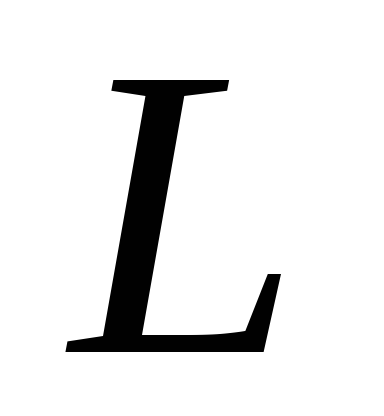 включается последовательно с резистором
переменного сопротивления в цепь с
источником постоянного напряжения
величиной
включается последовательно с резистором
переменного сопротивления в цепь с
источником постоянного напряжения
величиной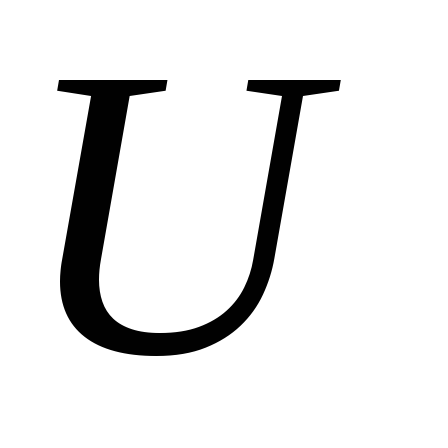 .
До момента
.
До момента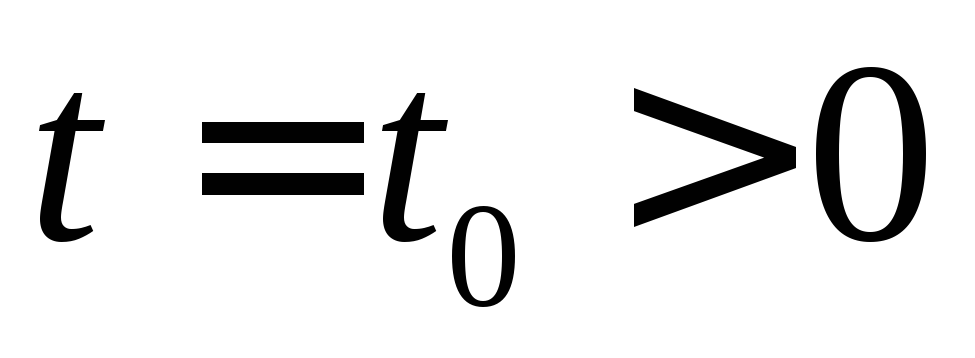 по цепи протекал постоянный ток, а
сопротивление резистора было равно
по цепи протекал постоянный ток, а
сопротивление резистора было равно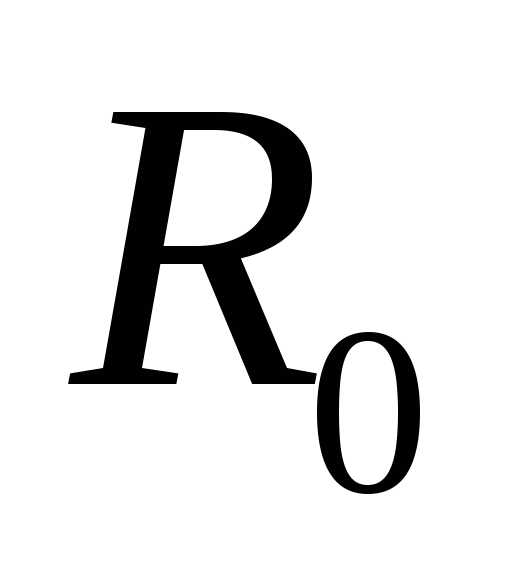 .
С момента
.
С момента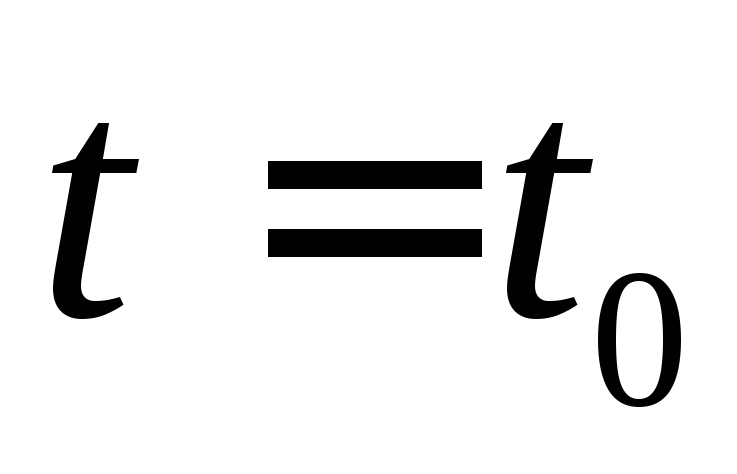 до
до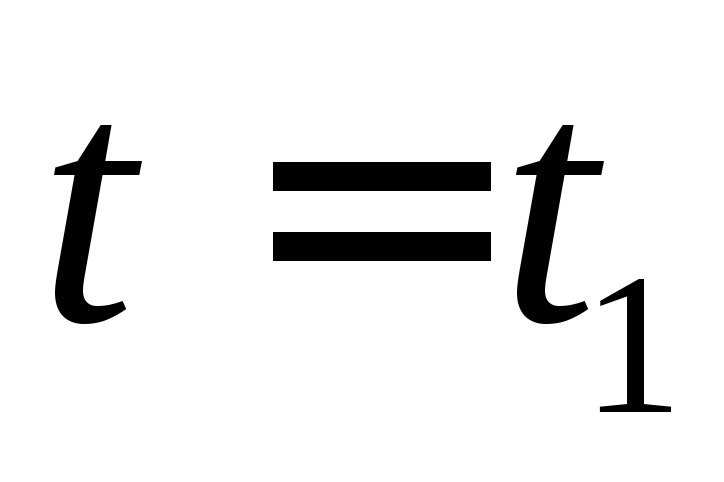 сопротивление резистора уменьшается
обратно пропорционально времени.
Найти ток
сопротивление резистора уменьшается
обратно пропорционально времени.
Найти ток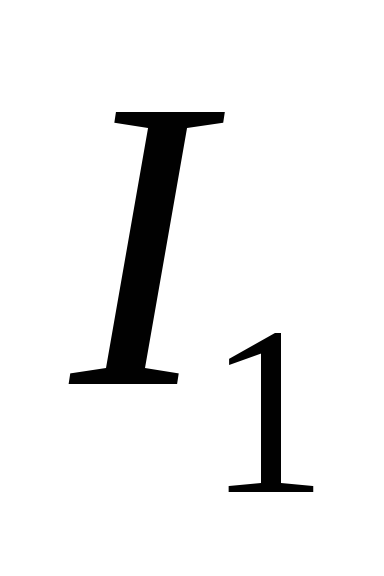 в катушке в момент времени
в катушке в момент времени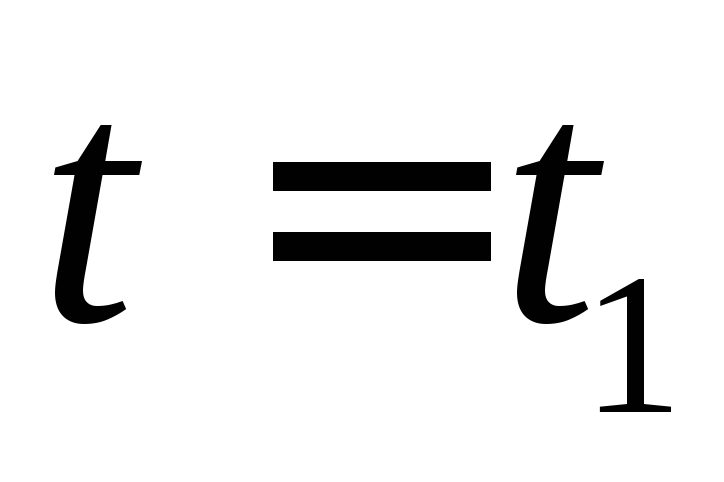 .
.Футбольный мяч, летящий горизонтально, ударяется о вертикальную стенку, при этом максимальная глубина его вмятины при деформации во время удара составляет
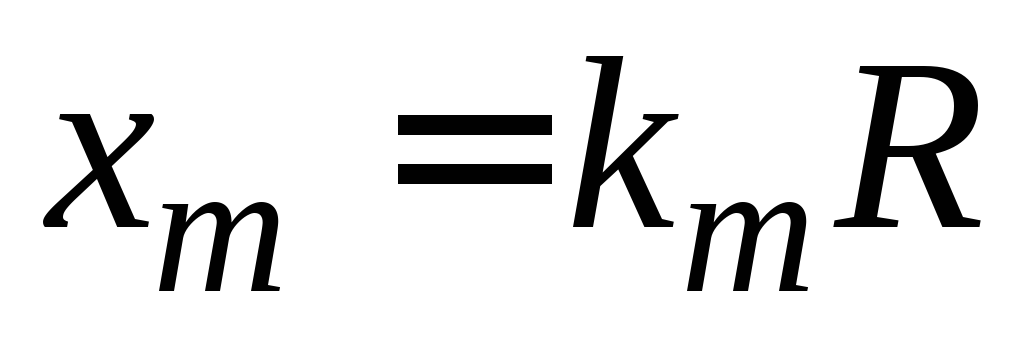 ,
где
,
где – радиус мяча. Найти зависимость
скорости
– радиус мяча. Найти зависимость
скорости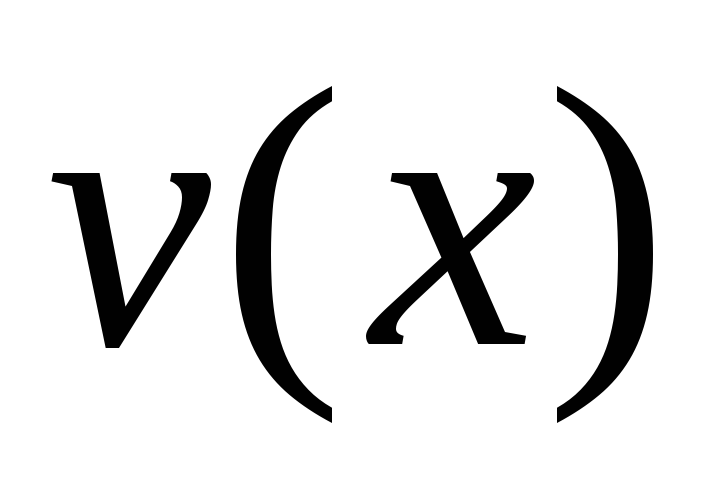 мяча от глубины вмятины
мяча от глубины вмятины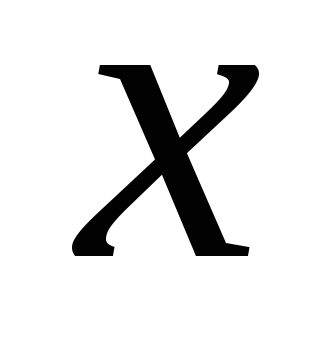 во время удара о стену. Зависимостью
давления
во время удара о стену. Зависимостью
давления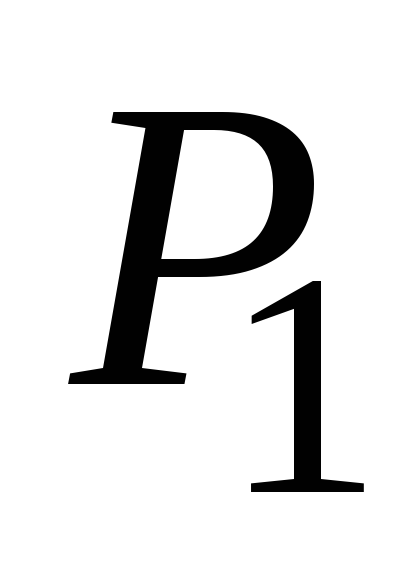 внутри мяча от глубины вмятины
пренебречь; также считать, что части
поверхности мяча, не соприкасающиеся
со стеной, не деформируются. Найти
скорость
внутри мяча от глубины вмятины
пренебречь; также считать, что части
поверхности мяча, не соприкасающиеся
со стеной, не деформируются. Найти
скорость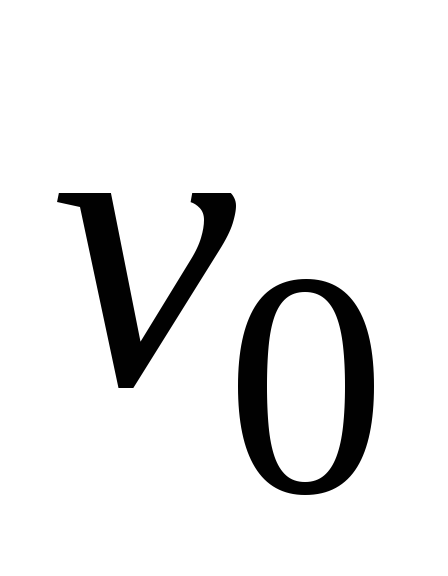 ,
с которой летел мяч до удара, если
масса мяча
,
с которой летел мяч до удара, если
масса мяча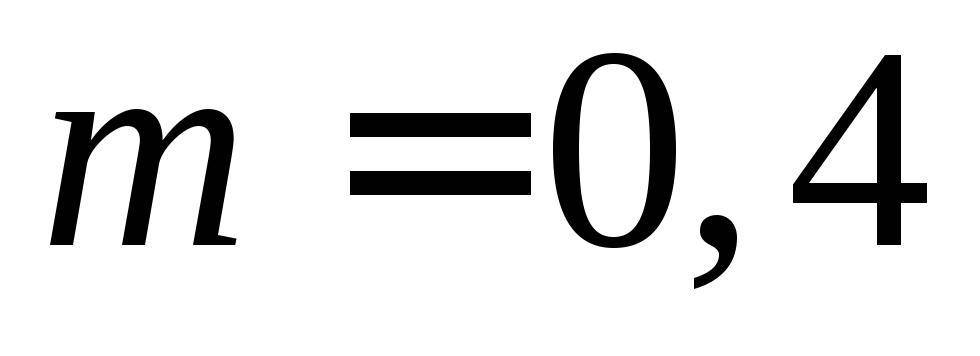 кг,
его радиус
кг,
его радиус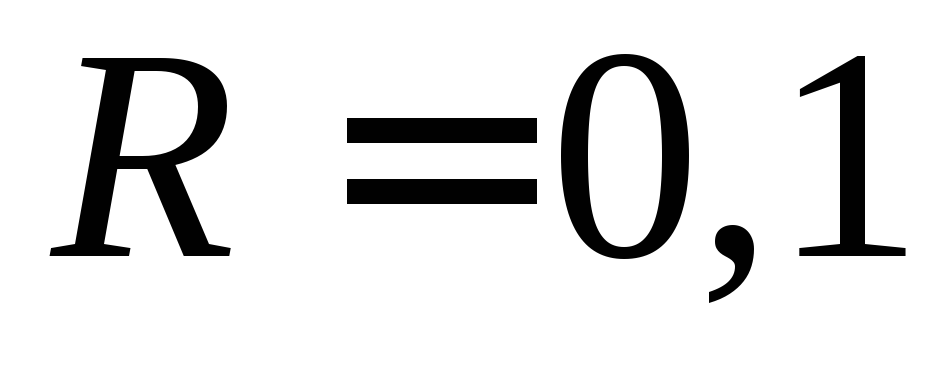 м,
разность между давлениями внутри и
снаружи мяча
м,
разность между давлениями внутри и
снаружи мяча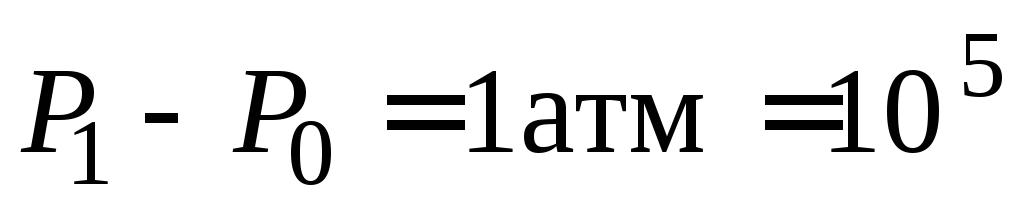 Па,
Па,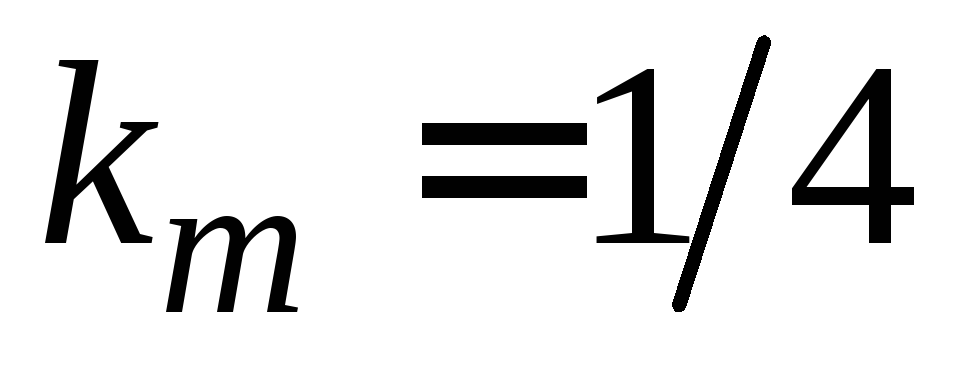 .
.Плоский конденсатор, одна из обкладок которого неподвижна, а другая удаляется от неё со скоростью
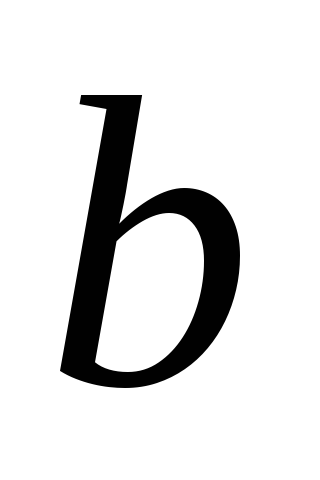 ,
подключён к источнику постоянного
напряжения
,
подключён к источнику постоянного
напряжения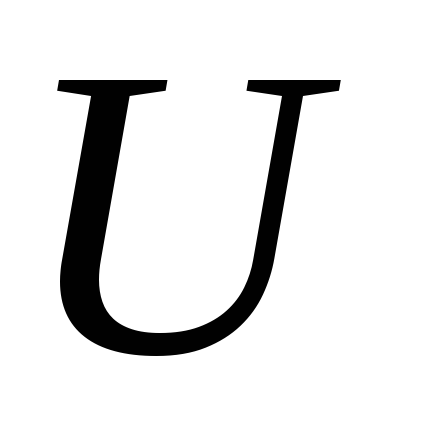 .
В момент, когда расстояние между
обкладками было равно
.
В момент, когда расстояние между
обкладками было равно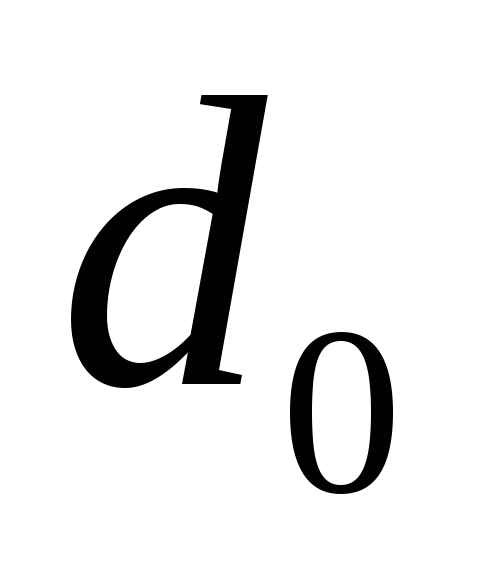 ,
от неподвижной обкладки оторвалась
пылинка массой
,
от неподвижной обкладки оторвалась
пылинка массой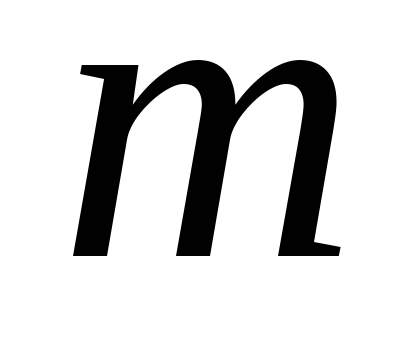 с зарядом
с зарядом и начала двигаться к другой обкладке.
Найти зависимость скорости пылинки
от времени, прошедшего с момента
отрыва. Сопротивлением воздуха,
краевыми эффектами и силой тяжести
пренебречь.
и начала двигаться к другой обкладке.
Найти зависимость скорости пылинки
от времени, прошедшего с момента
отрыва. Сопротивлением воздуха,
краевыми эффектами и силой тяжести
пренебречь.
