1.7. Нахождение уравнений кривых с помощью дифференциальных уравнений 1-го порядка

Для нахождения уравнений кривых с помощью дифференциальных уравнений 1-го порядка по заданным геометрическим свойствам кривых составляют уравнение , связывающее координаты произвольной точкикривойи производную функции. Напомним, что геометрический смысл производной− тангенс угла наклона касательной к кривойв точке.

На рисунке 1.1 представлена некоторая кривая . Для произвольной точкиэтой кривой построены касательнаяи нормальи выделены точки пересечения касательной и нормали с осямии, именно: а) для касательной – точкии; б) для нормали – точкии.

Геометрические свойства кривой обычно задаются условиями на соотношения между длинами отрезков,,,,,,и– отрезки касательной,– подкасательная,и– отрезки нормали,– поднормаль (см.рис.1.1). Каждое такое соотношение есть дифференциальное уравнение, определяющее совокупные геометрические свойства кривой. Решая уравнение, находят соответствующее семейство кривых с заданными свойствами. Задавая начальные условия, из семейства кривых выделяют единственную кривую.

Ниже приведены формулы длин основных характерных отрезковкривой,,,,,Величиной обозначен угловой коэффициент касательной в точке.

Запишем для точки уравнение касательной

(1.8)

и нормали

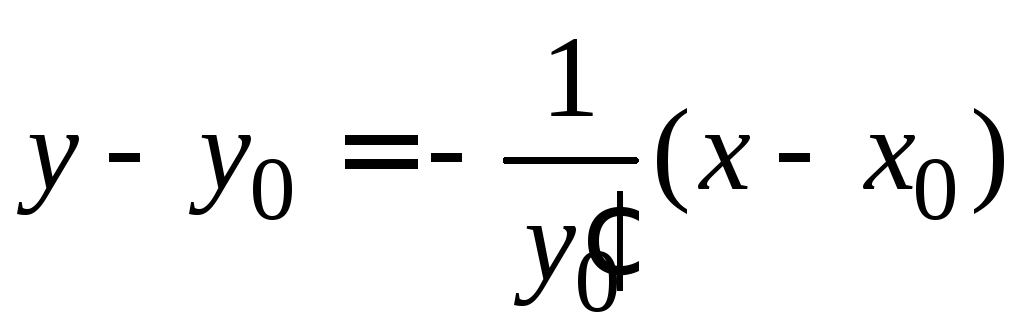.(1.9)

Используя (1.8), определим координаты точек ипересечения касательной с осями координат,и вычислим длины отрезков,:

а) для точки имеем:

=0 →=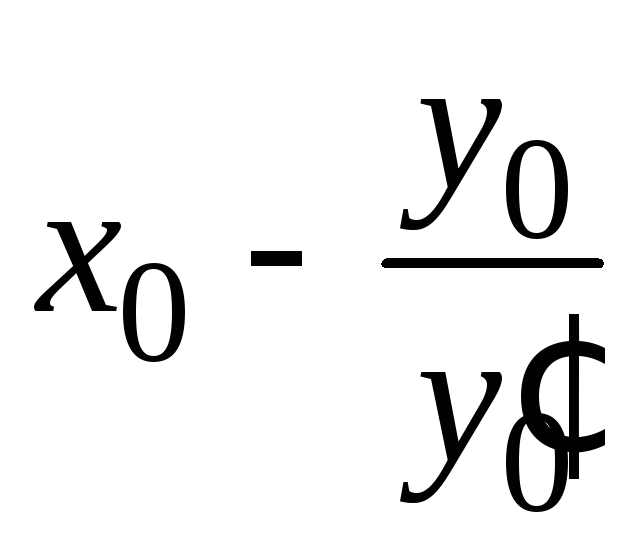→=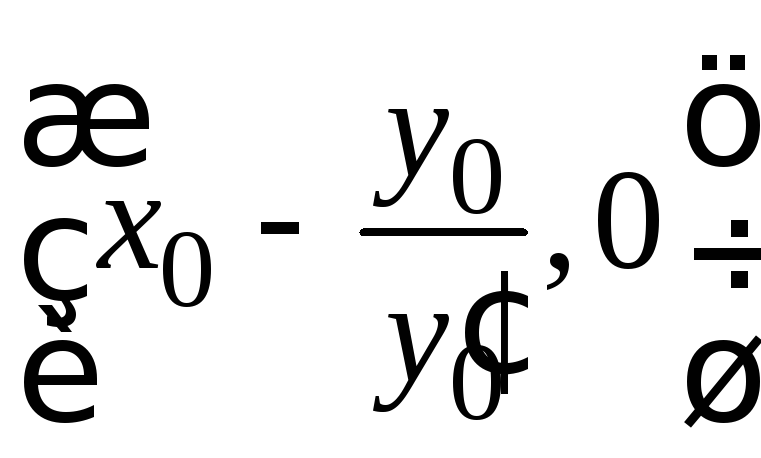→=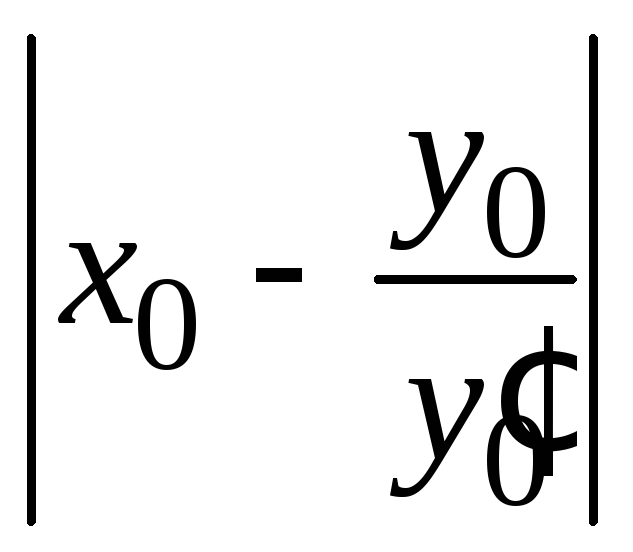; (1.10)

б) для точки имеем:

=0 →=→=→=. (1.11)

Зная координаты точки (см. (1.10)), вычислим длину подкасательной:

=

Аналогично, используя (1.9), найдем координаты точек ипересечения нормали с осями координат, и вычислим длины отрезков ,:

а) для точки имеем:

=0 →=→=→=; (1.12)

б) для точки имеем:

=0 →=→=→=.

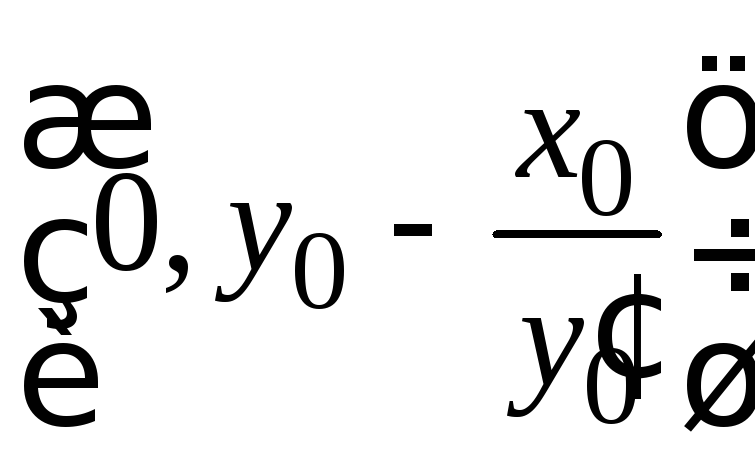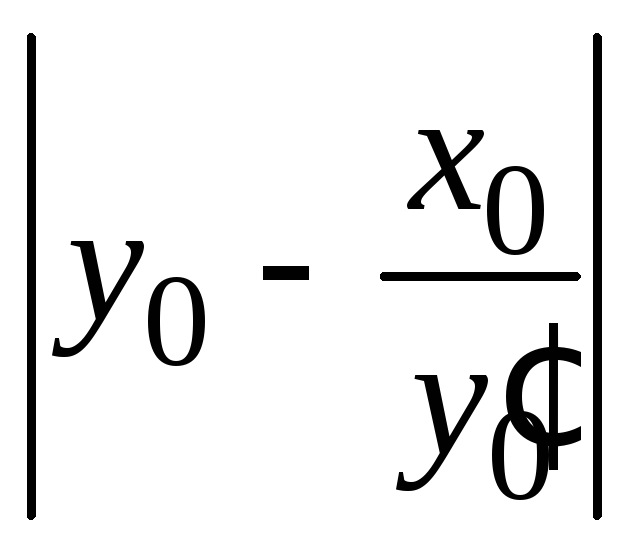Используя (1.12), вычислим длину поднормали =.

Пример 1.7.Найти уравнения кривых, проходящих через точку (1,1), зная, что длина отрезка, отсекаемого на оси ординат касательной к кривой в каждой точке, пропорциональна ординате точки касания. Принять коэффициент пропорциональности=2.

Решение. Пусть – произвольная точка кривой (см.рис.1.2). Считаем, так как ордината должна быть пропорциональна неотрицательной величине – длине отрезка. Условие задачи означает, что длина отрезкаравна 2, то есть, применяя формулу (1.11) для вычисления длины отрезка,=2.

Из равенства =2следует, что необходимо рассмотреть два случая:

▪ Случай-1: ; _(1.13)

▪ Случай-2: . _(1.14)

Случай-1.

1) Дифференциальное уравнение (1.13) имеет решением функцию , график которой не проходит через точку (1,1).

2) Запишем уравнение (1.13) в виде– это уравнение с разделяющимися переменными, общим решением которого является семейство гипербол. Требованиеозначает если, то, если, то(см.рис.1.3). Точкавыделяет из семейства гипербол единственную кривую.

Случай-2.

1) Перепишем уравнение (1.14) в виде . Нетрудно получить его общее решение– семейство кубических парабол. Здесь также если, то, если, то_. Кубическая парабола проходит через точкупри=1 (см.рис.1.4; для значенийсемейство интегральных кривых не показано).

Ответ. ,.

Задание 1.7. Найти уравнения кривых.

Замечания. 1) При оформлении решений заданий изобразите на рисунке 3-4 кривые из семейства, соответствующих общему решению дифференциального уравнения, и среди них выделите частное решение: линию, проходящую через заданную точку.

2) Используя кривую частного решения, покажите на чертеже касательную и подкасательную, нормаль и поднормаль для заданной точки .

1.7.1.Найти уравнение линии, проходящей через точку, зная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания:.

1.7.2.Найти уравнение линии, проходящей через точку, зная, что угловой коэффициент её касательной в этой точке равен абсциссе точки касания, умноженной на 2.

1.7.3.Найти уравнение линии, проходящей через точку, зная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания. Рассмотреть только случай, когда в каждой точке кривой.

1.7.4.Найти уравнение линии, проходящей через точку, зная, что длина её подкасательной для каждой точки кривой равна ординате точки касания. Рассмотреть только случай, когда в каждой точке кривой.

1.7.5.Найти уравнение линии, проходящей через точку, зная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания. Рассмотреть только случай, когда в каждой точке кривой.

1.7.6.Найти уравнение линии, проходящей через точку, зная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания.

1.7.7.Найти уравнение линии, проходящей через точку, зная, что угловой коэффициент её касательной в этой точке равен абсциссе точки касания, умноженной на 4.

1.7.8.Найти уравнение линии, проходящей через точку, зная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания. Рассмотреть только случай, когда в каждой точке кривой.

1.7.9.Найти уравнение линии, проходящей через точку, зная, что длина её подкасательной для каждой точки кривой равна ординате точки касания. Рассмотреть только случай, когда в каждой точке кривой.

1.7.10.Найти уравнение линии, проходящей через точку, зная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания. Рассмотреть только случай, когда в каждой точке кривой.

1.7.11.Найти уравнение линии, проходящей через точку, зная, что длина её поднормали для каждой точки кривой равна ординате точки касания. Рассмотреть только случай, когда в каждой точке кривой.

1.7.12.Найти уравнение линии, проходящей через точку, зная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания.

1.7.13.Найти уравнение линии, проходящей через точку, зная, что угловой коэффициент её касательной в этой точке равен абсциссе точки касания, умноженной на −2.

1.7.14.Найти уравнение линии, проходящей через точку, зная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой.

1.7.15.Найти уравнение линии, проходящей через точку, зная, что длина её подкасательной для каждой точки кривой равна ординате точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой.

1.7.16.Найти уравнение линии, проходящей через точку, зная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой.

1.7.17.Найти уравнение линии, проходящей через точку, зная, что длина её поднормали для каждой точки кривой равна ординате точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой.

1.7.18.Найти уравнение линии, проходящей через точку, зная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания.

1.7.19.Найти уравнение линии, проходящей через точку, зная, что угловой коэффициент её касательной в этой точке равен ординате точки касания, умноженной на 2.

1.7.20.Найти уравнение линии, проходящей через точку, зная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой.

1.7.21.Найти уравнение линии, проходящей через точку, зная, что длина её подкасательной для каждой точки кривой равна ординате точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой.

1.7.22.Найти уравнение линии, проходящей через точку, зная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой.

1.7.23.Найти уравнение линии, проходящей через точку, зная, что длина её поднормали для каждой точки кривой равна ординате точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой.

1.7.24.Найти уравнение линии, проходящей через точку, зная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания.

1.7.25.Найти уравнение линии, проходящей через точку, зная, что угловой коэффициент её касательной в этой точке равен ординате точки касания, умноженной на −2.

1.7.26.Найти уравнение линии, проходящей через точку, зная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания, умноженной на −2. Рассмотреть только случай, когда в каждой точке кривой.

1.7.27.Найти уравнение линии, проходящей через точку, зная, что длина её подкасательной для каждой точки кривой равна ординате точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой.

1.7.28.Найти уравнение линии, проходящей через точку, зная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания, умноженной на −2. Рассмотреть только случай, когда в каждой точке кривой.

1.7.29.Найти уравнение линии, проходящей через точку, зная, что длина её поднормали для каждой точки кривой равна ординате точки касания, умноженной на −2. Рассмотреть только случай, когда в каждой точке кривой.

1.7.30.Найти уравнение линии, проходящей через точку, зная, что угловой коэффициент её касательной в этой точке равен квадрату абсциссы точки касания, умноженной на 2.