1.5. Дифференциальное уравнение Бернулли

Дифференциальное уравнение называют уравнением Бернулли, если оно имеет вид

, (1.6)

причём, в выражении (1.6) требуем, чтобы не равнялось 0 или 1, так как при этих значениях уравнение (1.6) есть линейное уравнение. Заметим, что в случае>0 сразу выделяется одно из решений уравнения=0.

Известно, что при помощи подстановки уравнение Бернулли превращается в линейное уравнение:

Применив стандартный алгоритм решения линейного уравнения, находят функцию . Затем из равенстванаходят решение исходного уравнения.

Пример 1.5.Решить дифференциальное уравнение Бернулли∙.

Решение.1) Заданное дифференциальное уравнение есть уравнение Бернулли для случая=. Функцияявляется его решением.

2) Считая , перепишем заданное уравнение в виде. Применив подстановку=,,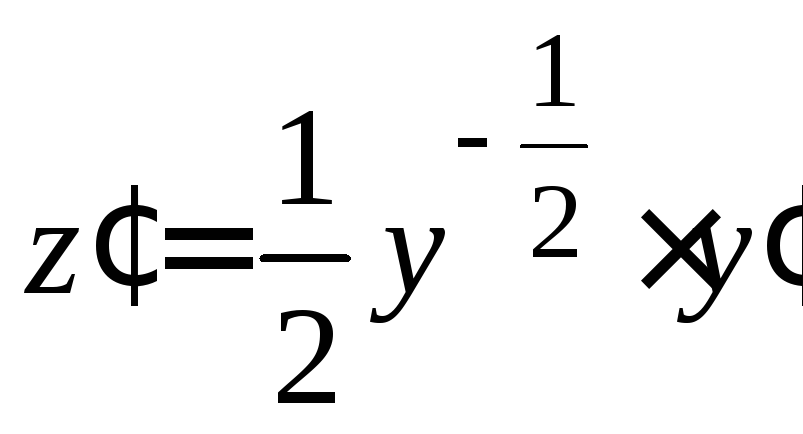 получаем линейное дифференциальное уравнение, гдеи.

3) Полагая , перепишем заданное уравнение=.

4) Потребуем, чтобы . Это уравнение с разделяющимися переменными. Его частное решение=, или=.

5) Теперь, интегрируя уравнение , получаем =+=+.

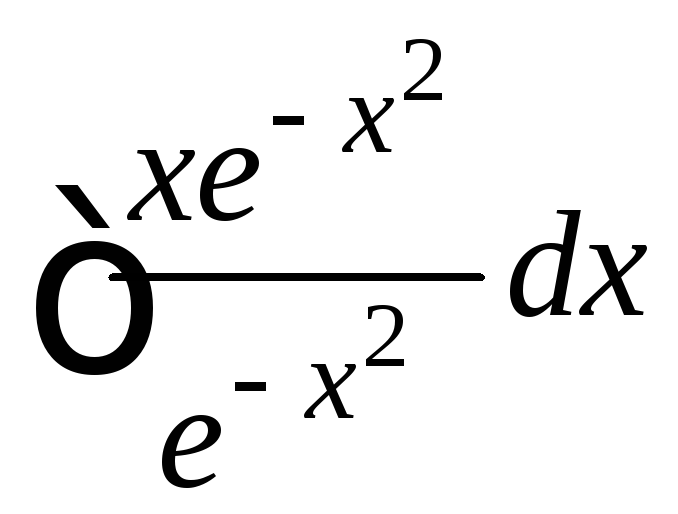6) Таким образом, =∙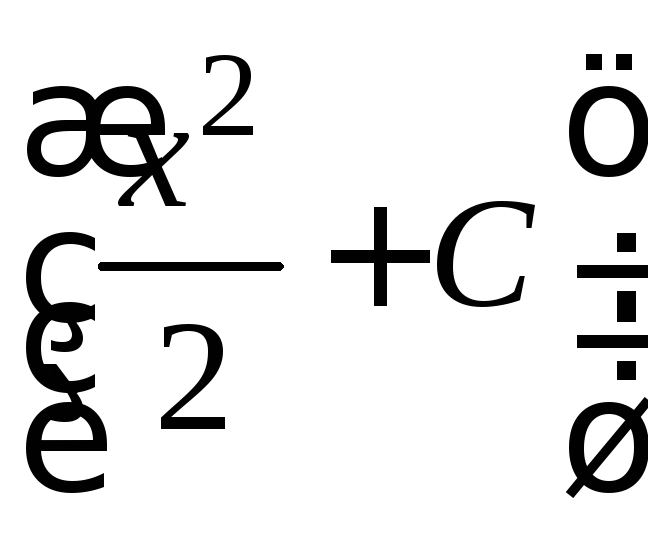. Так как=, получаем решение заданного уравнения=∙.

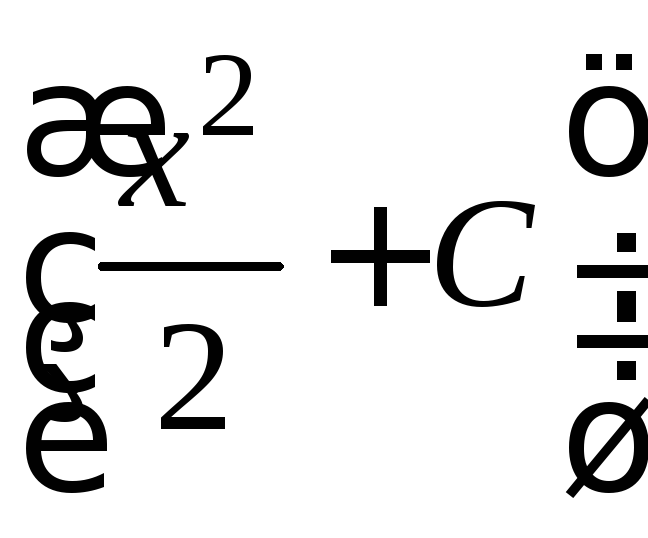Ответ.=·, .

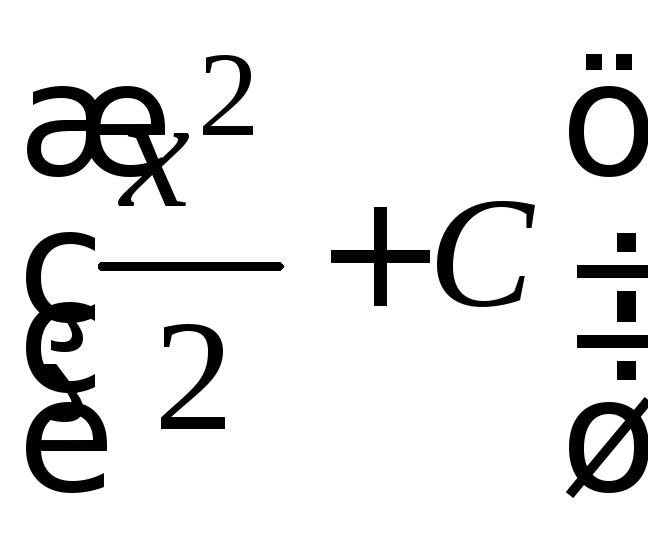Задание 1.5. Решить уравнение Бернулли.

Вар.	Уравнение:	Вар.	Уравнение:
1.5.1.	.	1.5.16.	.
1.5.2.	.	1.5.17.	.
1.5.3.	.	1.5.18.	.
1.5.4.	.	1.5.19.	.
1.5.5.	.	1.5.20.	.
1.5.6.	.	1.5.21.	.
1.5.7.	.	1.5.22.	.
1.5.8.	.	1.5.23.	.
1.5.9.	.	1.5.24.	.
1.5.10.	.	1.5.25.	.
1.5.11.	.	1.5.26.	.
1.5.12.	.	1.5.27.	.
1.5.13.	.	1.5.28.	.
1.5.14.	.	1.5.29.	.
1.5.15.	.	1.5.30.	.

1.6. Дифференциальные уравнения в полных дифференциалах

Если для дифференциального уравнения выполнено условие=, его называют уравнением в полных дифференциалах: в этом случае существует функция, для которой выражениеявляется ее полным дифференциалом. Так как полный дифференциал функции имеет вид, то должны выполняться равенстваи. Если функциянайдена, то равенство=, где− произвольная постоянная величина, задает семейство решений дифференциального уравнения в полных дифференциалах.

Для нахождения функции используют стандартный алгоритм, который иллюстрирует приведённый ниже пример.

Пример 1.6. Решить уравнение, предварительно удостоверившись, что заданное дифференциальное уравнение является уравнением в полных дифференциалах.

Решение.1) Вычислим производные=3 и=3. Равенство=подтверждено, это значит, что заданное уравнение есть уравнение в полных дифференциалах.

2) Учитывая, что , вычислим=+. В нашем случае имеем:

=+ =+. (1.7)

3) Вычислим производную =–. В нашем случае, учитывая заданное уравнением выражениеи (1.7), получаем=.

4) Интегрируя, находим функцию ==.

5) Подставляя в (1.7), записываем общее решение заданного уравнения

=+==.

Ответ.==.

Задание 1.6. Решить уравнение, предварительно проверив, что заданное дифференциальное уравнение является уравнением в полных дифференциалах.

Вар.	Уравнение:	Вар.	Уравнение:
1.6.1.		1.6.16.
1.6.2.		1.6.17.
1.6.3.		1.6.18.
1.6.4.		1.6.19.
1.6.5.		1.6.20.
1.6.6.		1.6.21.
1.6.7.		1.6.22.
1.6.8.		1.6.23.
1.6.9.		1.6.24.
1.6.10.		1.6.25.
1.6.11.		1.6.26.
1.6.12.		1.6.27.
1.6.13.		1.6.28.
1.6.14.		1.6.29.
1.6.15.		1.6.30.
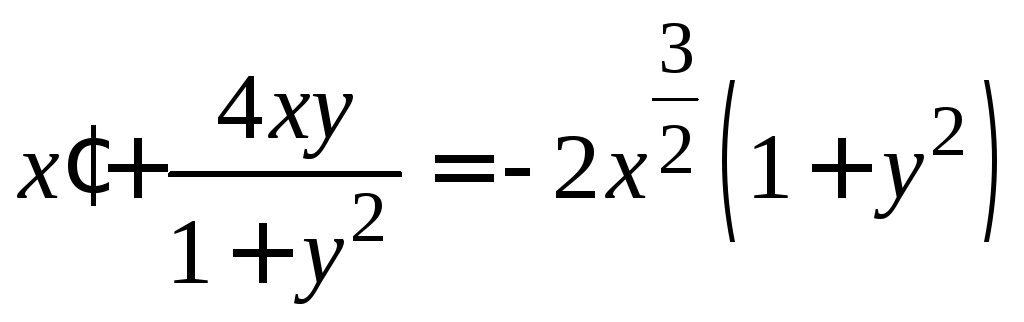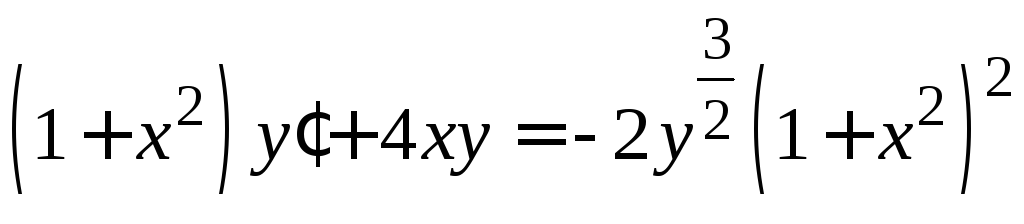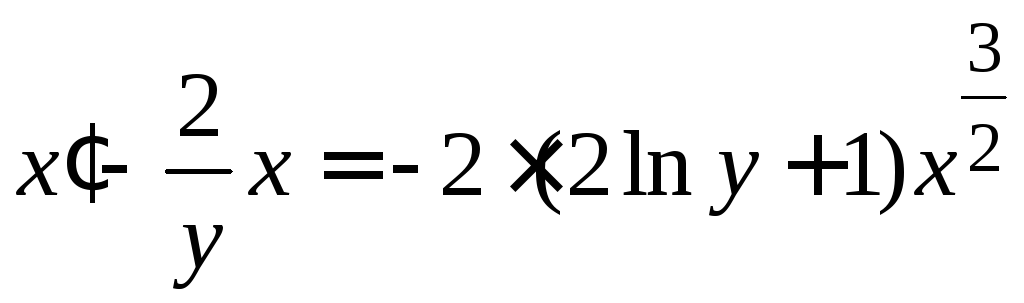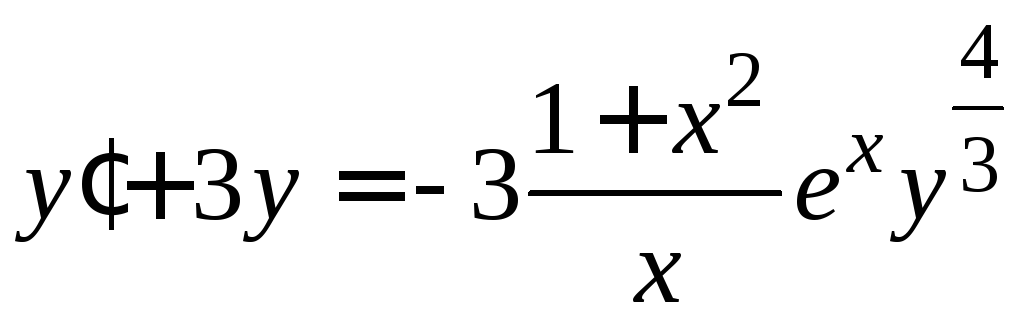