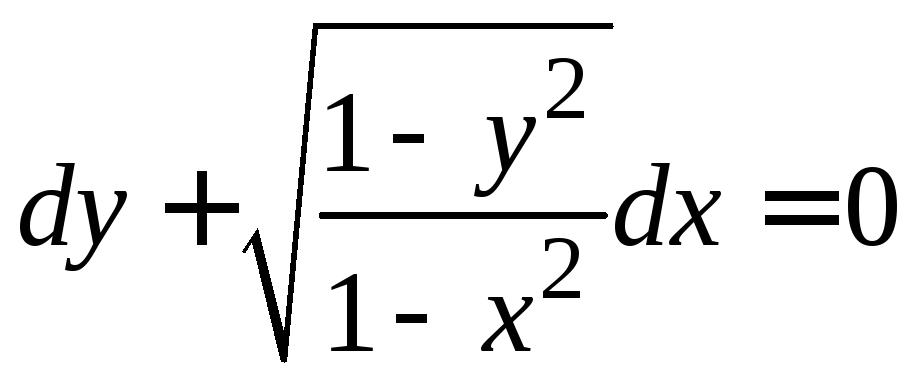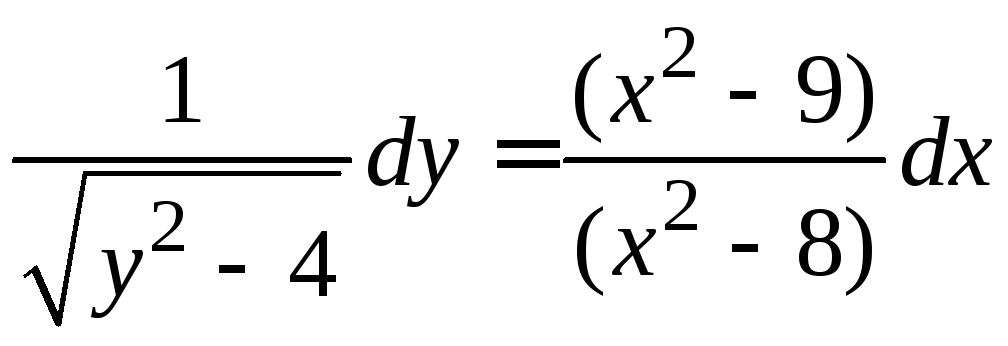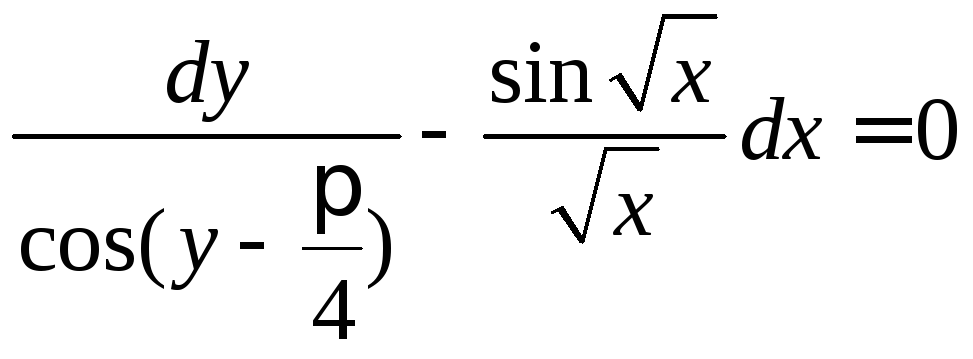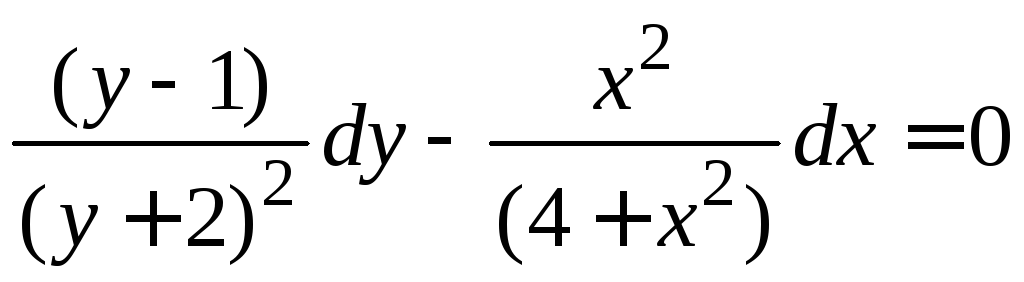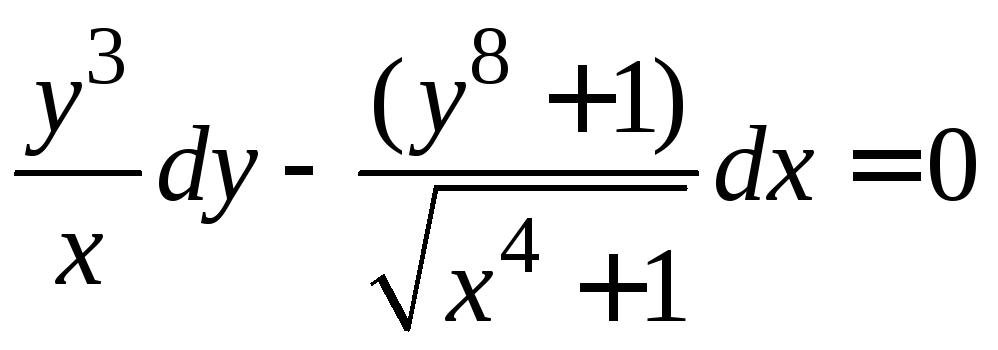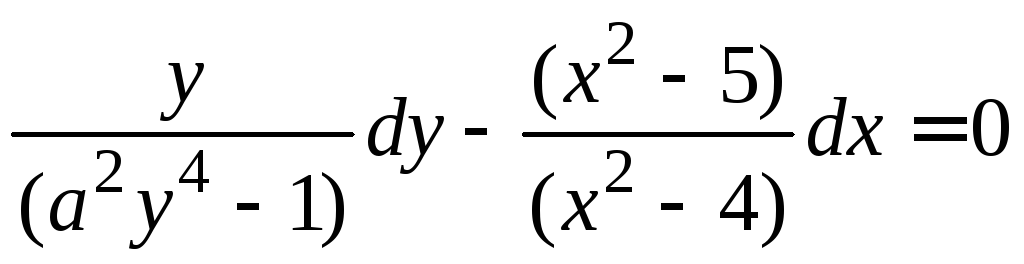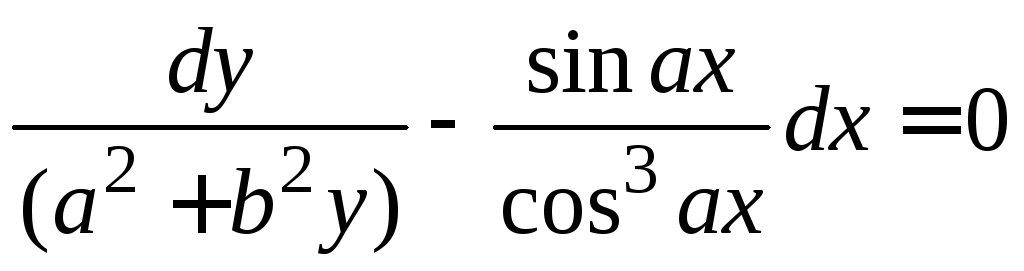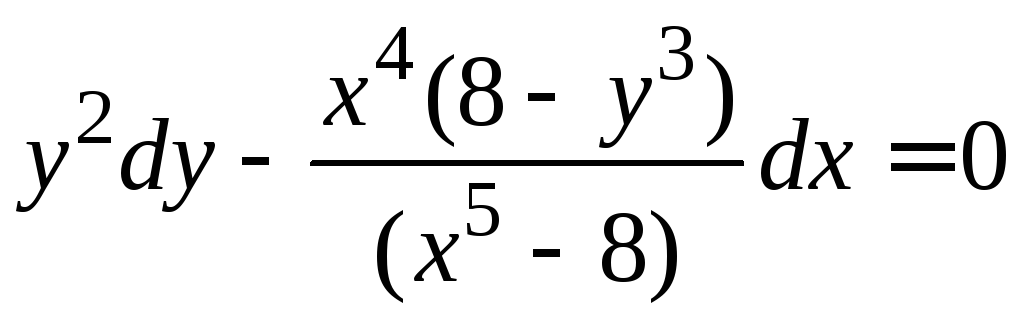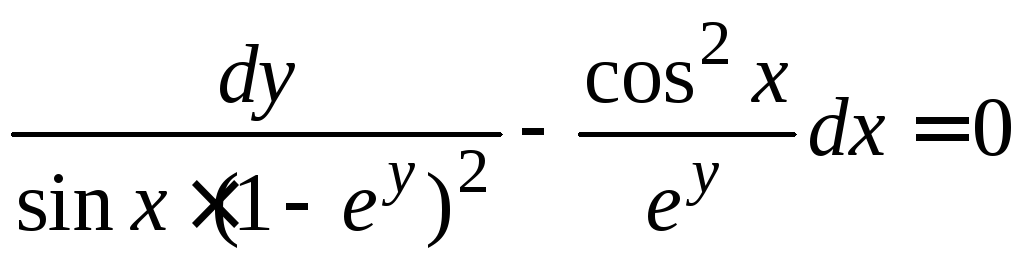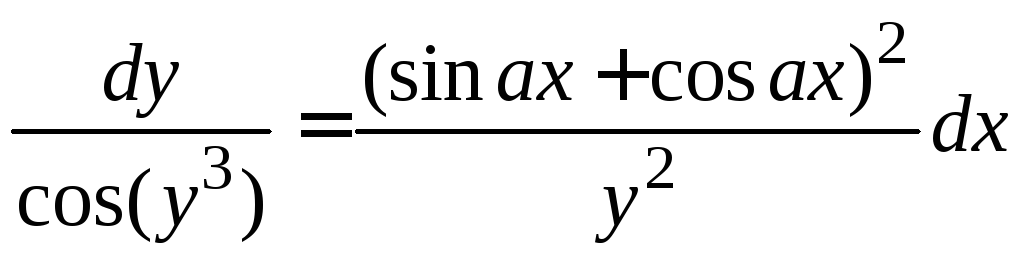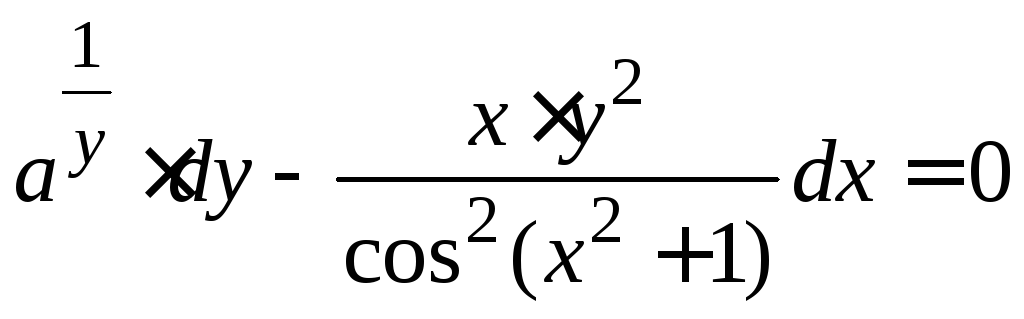1. Дифференциальные уравнения 1-го порядка

1.1. Дифференциальные уравнения семейства кривых

Пусть задано семейство кривых: , где- параметр. Необходимо составить дифференциальное уравнение, решением которого является это семейство.

Общая схема решения этой задачи:

1) Равенство определяет неявную функцию. Тогда на некотором промежутке справедливо тождество:. Дифференцируя это тождество по переменной, получим:===0.

2) Запишем систему 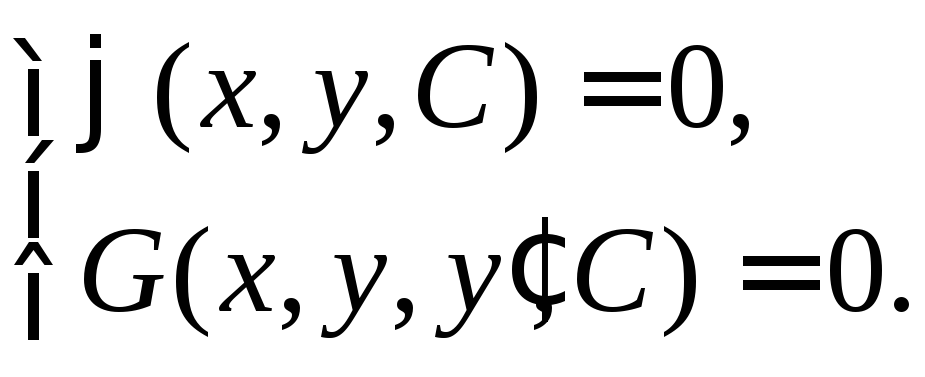Исключив параметриз этой системы, получим дифференциальное уравнение, решением которого является семейство кривых:.

Пример 1.1.Имеем семейство кривых:. Необходимо построить дифференциальное уравнение, для которого данное семейство кривых является решением.

Решение: 1) Считая, что выражение определяет неявную функцию,продифференцируем это выражение по независимой переменной. Имеем.

2) Запишем систему 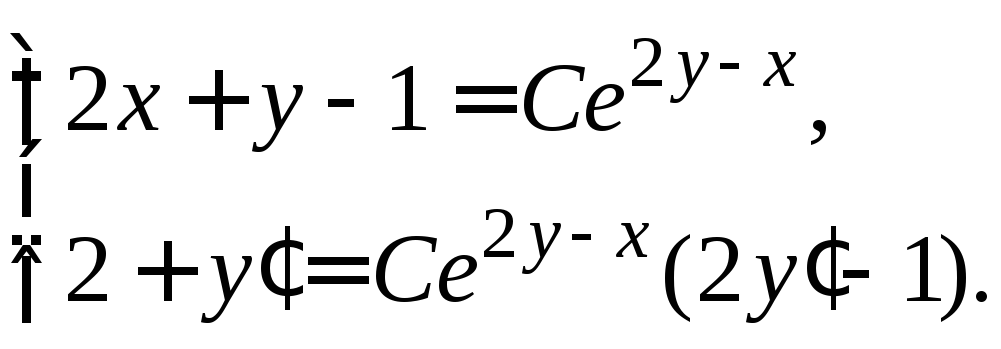Для исключения из системы параметраумножим первое уравнение наи приравняем левые части первого и второго равенств. Получим дифференциальное уравнение, или, решением которого является заданное семейство кривых.

Ответ..

Задание 1.1. Составить дифференциальное уравнение для семейства кривых.

Вар.	Семейство:	Вар.	Семейство:
1.1.1.	.	1.1.16.	.
1.1.2.	.	1.1.17.	.
1.1.3.	.	1.1.18.	.
1.1.4.	.	1.1.19.	.
1.1.5.	.	1.1.20.	.
1.1.6.	.	1.1.21.	.
1.1.7.	.	1.1.22.	.
1.1.8.	.	1.1.23.	.
1.1.9.	.	1.1.24.	.
1.1.10.	.	1.1.25.	.
1.1.11.	=.	1.1.26.	.
1.1.12.	.	1.1.27.	.
1.1.13.	.	1.1.28.	.
1.1.14.	.	1.1.29.	.
1.1.15.	.	1.1.30.	.

1.2. Дифференциальные уравнения с разделяющимися переменными

Известно, что в общем случае дифференциальное уравнение с разделяющимися переменными может быть представлено в виде:

. (1.1)

Для интегрирования уравнения переменные идолжны быть разделены. Для этого требуется разделить равенство (1.1) на произведение. В результате получим:

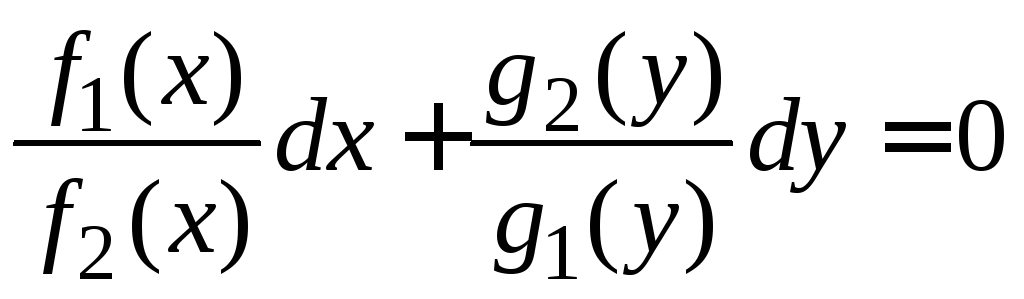. (1.2)

Интегрируя (1.2), находим общее решение исходного уравнения (1.1) в виде выражения: .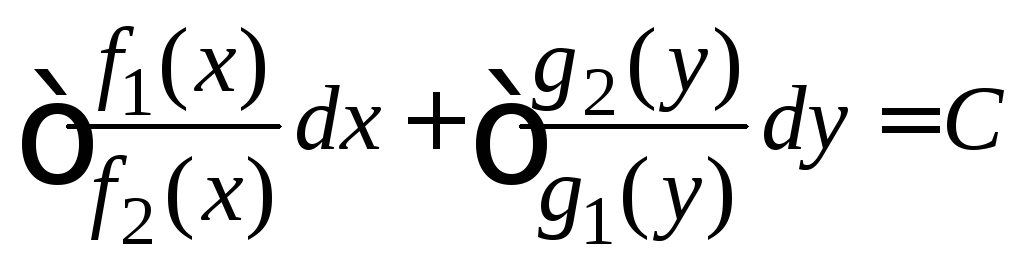

Для перехода к записи (1.2) выполнялось деление на функции: и. Если возможны равенстваи, необходимо функциииучесть как решения исходного уравнения.

Пример 1.2.Решить дифференциальное уравнение.

Решение.1) Заданное уравнение есть уравнение с разделяющимися переменными, гдеи. Так каки, то функцииинеобходимо учесть как решения исходного уравнения.

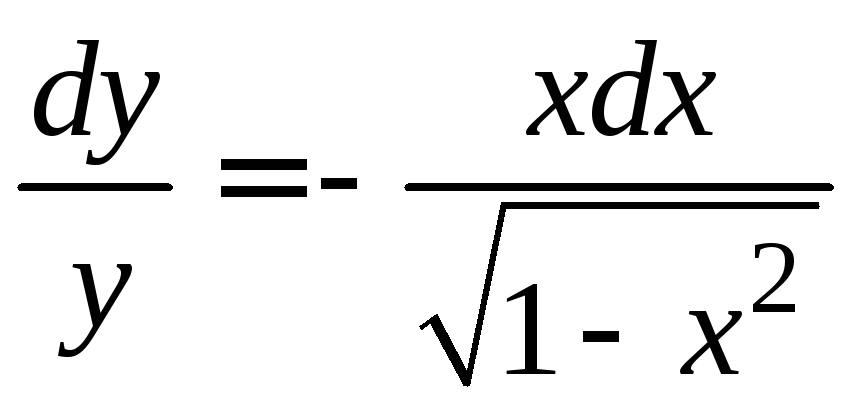2) Теперь считаем, что . Разделив заданное уравнение на , получим уравнение с разделенными переменными.

3) В результате интегрирования находим общее решение уравнения в виде или . Учитывая, что − произвольная постоянная величина, запишем общее решение в виде . При =0 из общего решения получаем также решение .

Ответ.;.

Задание 1.2. Решить уравнение с разделяющимися переменными.

Вар.	Уравнение:	Вар.	Уравнение:
1.2.1.		1.2.16.
1.2.2.		1.2.17.
1.2.3.		1.2.18.
1.2.4.		1.2.19.
1.2.5.		1.2.20.
1.2.6.		1.2.21.
1.2.7.		1.2.22.
1.2.8.		1.2.23.
1.2.9.		1.2.24.
1.2.10.		1.2.25.
1.2.11.		1.2.26.
1.2.12.		1.2.27.
1.2.13.		1.2.28.
1.2.14.		1.2.29.
1.2.15.		1.2.30.
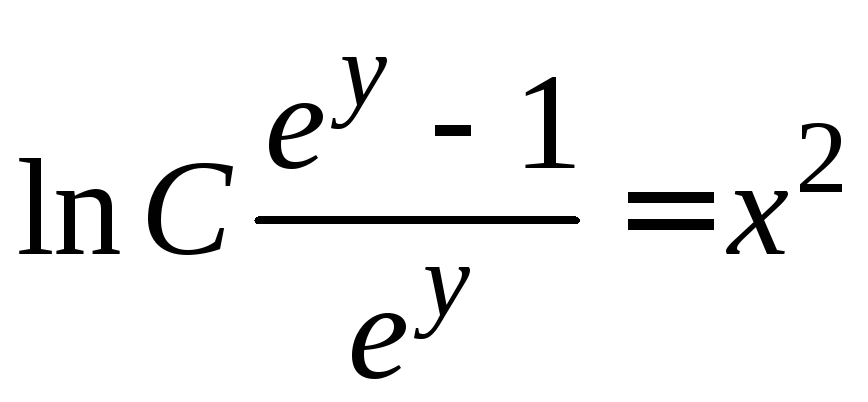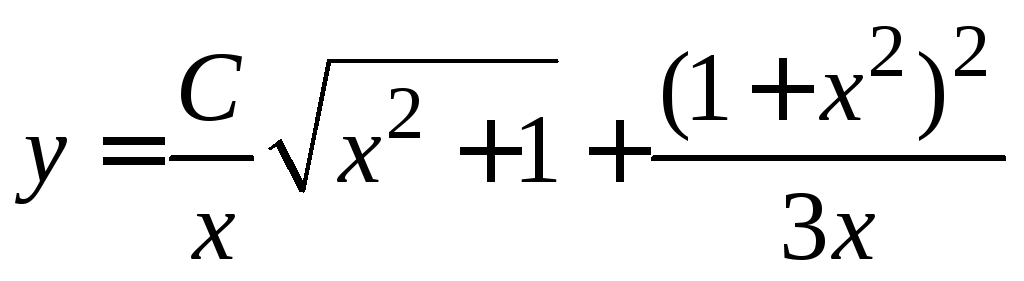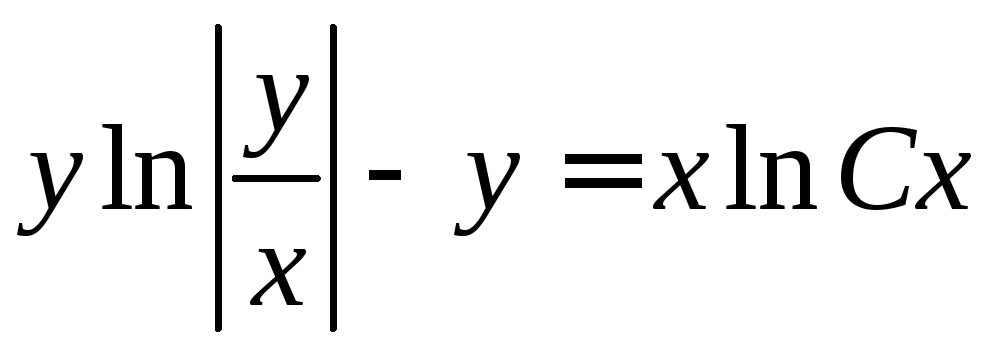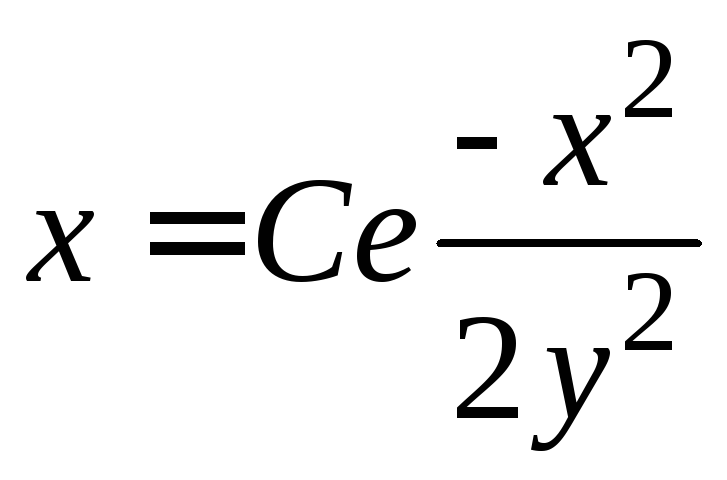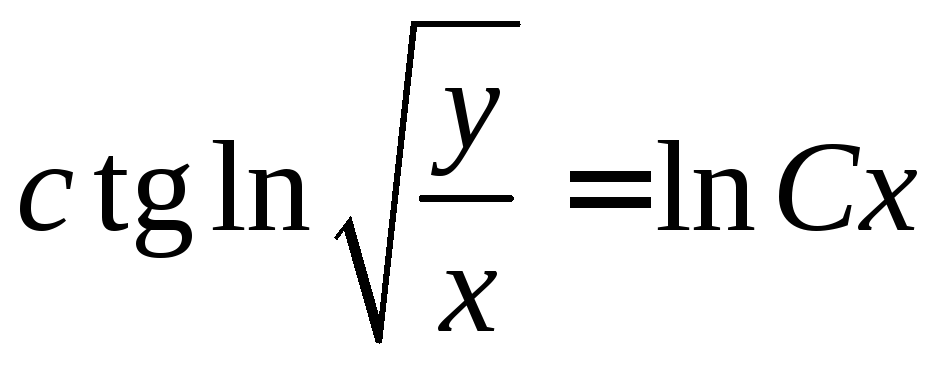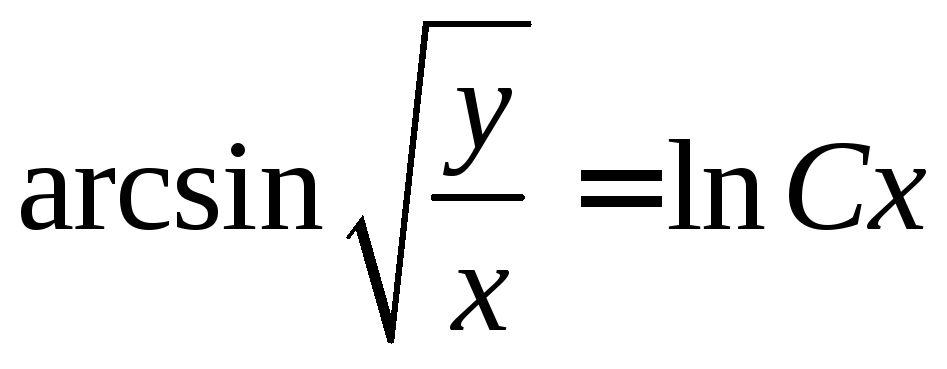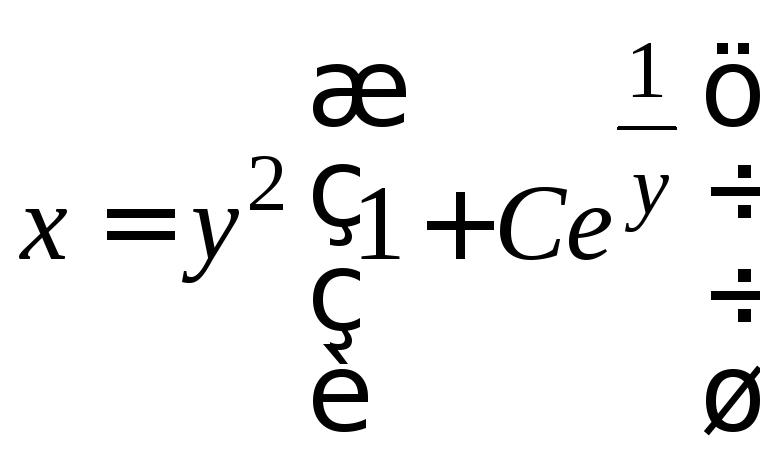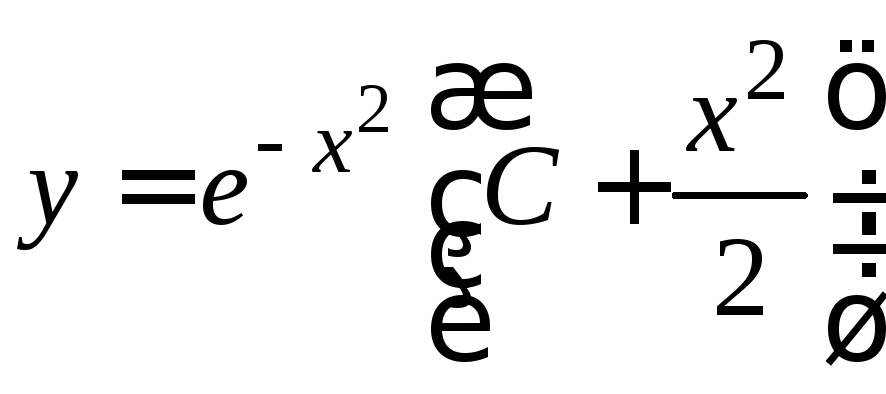