
- •2. Линейные дифференциальные уравнения
- •2.1. Линейные однородные дифференциальные уравнения 2-го порядка
- •2.2. Линейные однородные дифференциальные уравнения n-го порядка
- •2.3. Метод вариации произвольных постоянных решения неоднородных дифференциальных уравнений
- •2.4. Линейные неоднородные дифференциальные уравнения 2-го порядка с правой частью вида
- •2.5. Линейные неоднородные дифференциальные уравнения 2-го порядка с правой частью вида
- •2.6. Линейные неоднородные дифференциальные уравнения 3-го и 4-го порядков со специальной правой частью
- •2.7. Применение дифференциальных уравнений 2-го порядка для решения геометрических задач
- •2.8. Применение дифференциальных уравнений 2-го порядка для решения физических задач
- •2.9. Однородные и неоднородные уравнения Эйлера
2.8. Применение дифференциальных уравнений 2-го порядка для решения физических задач
Указание 1.В
задачах 2.8.4 и далее при расчёте силы
тяжести (или электростатической силы),
действующей на тело внутри другого тела
учитывать, что благодаря закону обратных
квадратов ускорение свободного падения
(напряжённость электростатического
поля) в точке, находящейся внутри
сферически симметричного тела на
расстоянии![]() от его центра, не зависит от массы
(заряда), находящейся снаружи сферы
радиуса
от его центра, не зависит от массы
(заряда), находящейся снаружи сферы
радиуса![]() .
.
Указание 2.В
задачах, где рассматривается вращение
с постоянной угловой скоростью, учесть,
что для использования 2-го закона Ньютона
во вращающейся с постоянной угловой
скоростью![]() системе отсчёта к реальным силам,
действующим на материальную точку,
нужно добавить также центробежную силу
системе отсчёта к реальным силам,
действующим на материальную точку,
нужно добавить также центробежную силу![]() (
(![]() – расстояние от материальной точки до
оси вращения), а также силу Кориолиса
– расстояние от материальной точки до
оси вращения), а также силу Кориолиса![]() ,
где
,
где![]() – скорость тела относительно вращающейся
системы отсчёта.
– скорость тела относительно вращающейся
системы отсчёта.
П ример
2.13.В диэлектрическом шаре радиусом
ример
2.13.В диэлектрическом шаре радиусом![]() ,
заряженном равномерно по объёму с
плотностью
,
заряженном равномерно по объёму с
плотностью![]() ,
просверлено сквозное диаметральное
отверстие. В этом отверстии движется
непроводящий стержень длиной
,
просверлено сквозное диаметральное
отверстие. В этом отверстии движется
непроводящий стержень длиной![]() с закреплёнными на его концах зарядами
с закреплёнными на его концах зарядами![]() и
и![]() в изолированной оболочке (рис.2.2). Общая
масса стержня с зарядами равна
в изолированной оболочке (рис.2.2). Общая
масса стержня с зарядами равна![]() ,
в момент времени
,
в момент времени![]() середина стержня находилась в центре
шара, скорость была равна нулю. Найти
зависимость от времени отклонения
середина стержня находилась в центре
шара, скорость была равна нулю. Найти
зависимость от времени отклонения![]() середины стержня от центра. Постоянная
закона Кулона
середины стержня от центра. Постоянная
закона Кулона![]() ,
трением о стенки отверстия, сопротивлением
воздуха пренебречь.
,
трением о стенки отверстия, сопротивлением
воздуха пренебречь.
Решение.1) На
заряды![]() и
и![]() действуют электростатические силы
действуют электростатические силы![]() и
и![]() соответственно со стороны распределённых
по объёму зарядов в шаре (см.рис.2.2),
взаимодействие зарядов
соответственно со стороны распределённых
по объёму зарядов в шаре (см.рис.2.2),
взаимодействие зарядов![]() и
и![]() между собой компенсируется упругими
силами стержня, соединяющего их, и не
влияет на движение стержня с зарядами.
УравнениеIIзакона Ньютона
для стержня будет иметь вид
между собой компенсируется упругими
силами стержня, соединяющего их, и не
влияет на движение стержня с зарядами.
УравнениеIIзакона Ньютона
для стержня будет иметь вид
![]() ,
(2.7)
,
(2.7)
где
![]() – радиус-вектор середины стержня.
Направим осьxиз
центра шара в сторону заряда
– радиус-вектор середины стержня.
Направим осьxиз
центра шара в сторону заряда![]() ,
тогда
,
тогда![]() и
и![]() – координаты зарядов
– координаты зарядов![]() и
и![]() .
В соответствии с законом обратных
квадратов, напряжённость электрического
поля, создаваемого зарядами шара, в
точке нахождения заряда
.
В соответствии с законом обратных
квадратов, напряжённость электрического
поля, создаваемого зарядами шара, в
точке нахождения заряда![]() зависит только от заряда, находящегося
внутри сферы, проходящей через
зависит только от заряда, находящегося
внутри сферы, проходящей через![]() (на рисунке показана штриховой линией).
Таким образом, для проекции силы
(на рисунке показана штриховой линией).
Таким образом, для проекции силы![]() на осьxполучим:
на осьxполучим:
 ,
,
где
![]() – сумма зарядов шара, находящихся внутри
сферы радиуса
– сумма зарядов шара, находящихся внутри
сферы радиуса![]() .
Поскольку
.
Поскольку![]() ,
то
,
то
![]() .
(2.8)
.
(2.8)
Аналогично, для
проекции силы
![]() на осьxимеем:
на осьxимеем:
![]() .
(2.9)
.
(2.9)
Подставляя (2.8) и (2.9) в проекцию уравнения (2.7) на ось xи учитывая соотношения
![]() ,
,![]() ,
,
получим дифференциальное уравнение
![]() .
(2.10)
.
(2.10)
2) Уравнение (2.10) линейное неоднородное с постоянными коэффициентами. Его общее решение
 .
.
Из начальных
условий найдём, что
![]() ,
поэтому искомая зависимость будет иметь
вид
,
поэтому искомая зависимость будет иметь
вид
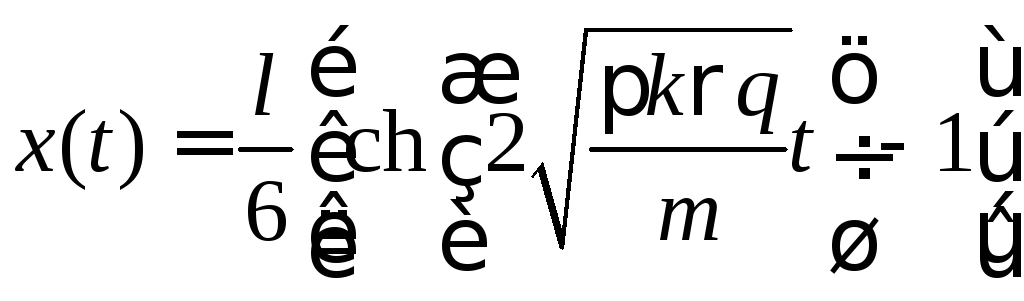 .
.
Ответ. .
.
2.8.1. Один конец
пружины жёсткостью
![]() закреплён неподвижно, а к другому
прикреплён груз массой
закреплён неподвижно, а к другому
прикреплён груз массой![]() .
При движении груз испытывает силу
сопротивления внешней среды,
пропорциональную скорости с коэффициентом
пропорциональности
.
При движении груз испытывает силу
сопротивления внешней среды,
пропорциональную скорости с коэффициентом
пропорциональности![]() .
При
.
При![]() грузу, находившемуся в положении
равновесия, сообщена скорость
грузу, находившемуся в положении
равновесия, сообщена скорость![]() .
Найти зависимость
.
Найти зависимость![]() отклонения груза от положения равновесия
от времени для случая
отклонения груза от положения равновесия
от времени для случая![]() .
.
Ответ. .
.
2.8.2. Решить задачу
2.8.1 при
![]() и дополнительном условии, что на груз
действует внешняя периодическая сила
и дополнительном условии, что на груз
действует внешняя периодическая сила![]() .
.
Ответ.
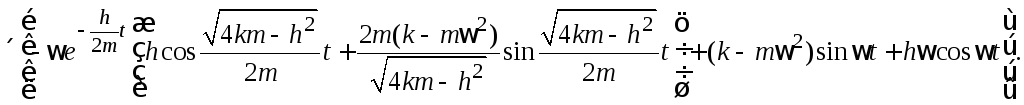
2.8.3. На конце
упругого стержня укреплена масса
![]() .
Другой конец стержня вибрирует так, что
его смещение в момент
.
Другой конец стержня вибрирует так, что
его смещение в момент![]() равно
равно![]() .
Упругая сила, возникающая в стержне,
пропорциональна разности смещений его
концов с коэффициентом
.
Упругая сила, возникающая в стержне,
пропорциональна разности смещений его
концов с коэффициентом![]() .
Найти амплитуду
.
Найти амплитуду![]() вынужденных колебаний массы
вынужденных колебаний массы![]() .
Может ли быть
.
Может ли быть![]() ?
Массой стержня и трением пренебречь.
?
Массой стержня и трением пренебречь.
Ответ. ;
может.
;
может.
2.8.4. На одном из
астероидов радиусом
![]() обнаружен сквозной прямолинейный канал,
проходящий через центр астероида. В
этот канал в момент
обнаружен сквозной прямолинейный канал,
проходящий через центр астероида. В
этот канал в момент![]() с поверхности было брошено без начальной
скорости тело. Считая плотность астероида
с поверхности было брошено без начальной
скорости тело. Считая плотность астероида![]() постоянной, найти зависимость
постоянной, найти зависимость![]() отклонения тела от центра астероида.
Гравитационная постоянная
отклонения тела от центра астероида.
Гравитационная постоянная![]() ,
трением о стенки канала, сопротивлением
атмосферного газа и вращением астероида
пренебречь.
,
трением о стенки канала, сопротивлением
атмосферного газа и вращением астероида
пренебречь.
Ответ. .
.
2.8.5. Решить задачу
2.8.4 с учётом силы сопротивления
атмосферного газа, которое пропорционально
скорости тела; коэффициент пропорциональности
считать не зависящим от глубины и равным
![]() .
.
Ответ. .
.
2.8.6. На некотором
астероиде радиусом
![]() обнаружен сквозной прямолинейный канал,
минимальное расстояние от которого до
центра астероида равно
обнаружен сквозной прямолинейный канал,
минимальное расстояние от которого до
центра астероида равно![]() .
В этот канал в момент
.
В этот канал в момент![]() с поверхности было брошено без начальной
скорости тело. Считая плотность астероида
с поверхности было брошено без начальной
скорости тело. Считая плотность астероида![]() постоянной, найти зависимость
постоянной, найти зависимость![]() отклонения тела от наиболее глубокой
точки канала внутри астероида.
Гравитационная постоянная
отклонения тела от наиболее глубокой
точки канала внутри астероида.
Гравитационная постоянная![]() ,
трением о стенки канала, сопротивлением
атмосферного газа и вращением астероида
пренебречь.
,
трением о стенки канала, сопротивлением
атмосферного газа и вращением астероида
пренебречь.
Ответ.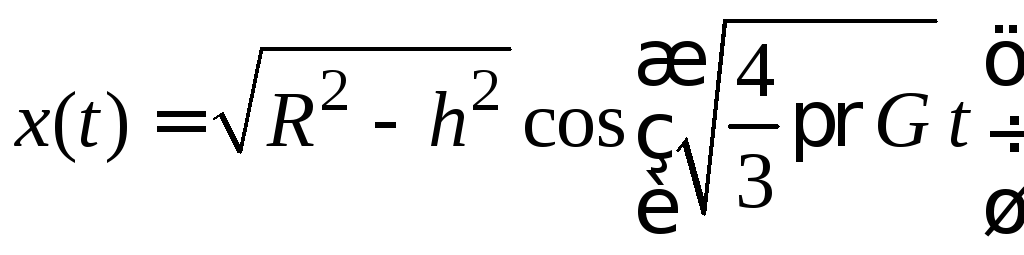 .
.
2.8.7. Решить задачу
2.8.6 с учётом силы трения скольжения о
стенки канала, коэффициент которого
считать постоянным и равным
![]() .
Рассмотреть случай движения от поверхности
в сторону наиболее глубокой точки
канала.
.
Рассмотреть случай движения от поверхности
в сторону наиболее глубокой точки
канала.
Ответ.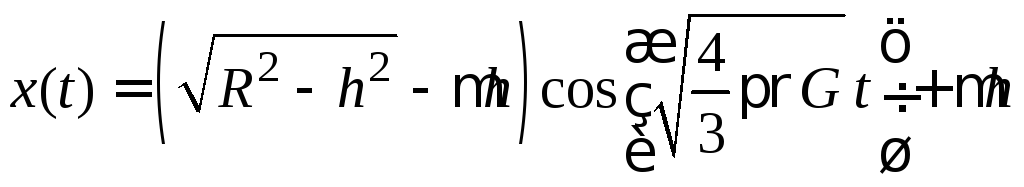 .
.
2.8.8. На некотором
астероиде радиусом
![]() обнаружен сквозной прямолинейный канал,
проходящий через центр астероида и
перпендикулярный оси вращения астероида.
В этот канал в момент
обнаружен сквозной прямолинейный канал,
проходящий через центр астероида и
перпендикулярный оси вращения астероида.
В этот канал в момент![]() с поверхности было брошено без начальной
скорости тело. Считая плотность астероида
с поверхности было брошено без начальной
скорости тело. Считая плотность астероида![]() постоянной, найти зависимость
постоянной, найти зависимость![]() отклонения тела от центра астероида,
если угловая скорость вращения астероида
равна
отклонения тела от центра астероида,
если угловая скорость вращения астероида
равна![]() .
Гравитационная постоянная
.
Гравитационная постоянная![]() ,
трением о стенки канала и сопротивлением
атмосферного газа пренебречь.
,
трением о стенки канала и сопротивлением
атмосферного газа пренебречь.
Ответ. .
.
2.8.9. Решить задачу
2.8.8. с учётом силы трения скольжения о
стенки канала, коэффициент которого
считать постоянным и равным
![]() .
Рассмотреть случай движения от поверхности
в сторону центра; считать, что
.
Рассмотреть случай движения от поверхности
в сторону центра; считать, что![]() .
.
Ответ.![]() ,
где
,
где![]() ,
,![]() .
.
2.8.10. Решить задачу
2.8.9 в случае, когда
![]() .
.
Ответ. .
.
2.8.11. На одном из
астероидов радиусом
![]() обнаружен сквозной прямолинейный канал,
перпендикулярный оси вращения астероида
и проходящий через неё. Минимальное
расстояние от канала до центра астероида
равно
обнаружен сквозной прямолинейный канал,
перпендикулярный оси вращения астероида
и проходящий через неё. Минимальное
расстояние от канала до центра астероида
равно![]() .
В этот канал в момент
.
В этот канал в момент![]() с поверхности было брошено без начальной
скорости тело. Считая плотность астероида
с поверхности было брошено без начальной
скорости тело. Считая плотность астероида![]() постоянной, найти зависимость
постоянной, найти зависимость![]() отклонения тела от наиболее глубокой
точки канала внутри астероида, если
угловая скорость вращения астероида
равна
отклонения тела от наиболее глубокой
точки канала внутри астероида, если
угловая скорость вращения астероида
равна![]() .
Рассмотреть случай движения от поверхности
в сторону центра. Гравитационная
постоянная
.
Рассмотреть случай движения от поверхности
в сторону центра. Гравитационная
постоянная![]() ,
трением о стенки канала, сопротивлением
атмосферного газа пренебречь.
,
трением о стенки канала, сопротивлением
атмосферного газа пренебречь.
Ответ. .
.
2.8.12. В диэлектрическом
шаре радиусом
![]() ,
заряженном равномерно по объёму с
плотностью
,
заряженном равномерно по объёму с
плотностью![]() ,
просверлено сквозное диаметральное
отверстие. С одной стороны в это отверстие
влетает со скоростью
,
просверлено сквозное диаметральное
отверстие. С одной стороны в это отверстие
влетает со скоростью![]() пылинка массой
пылинка массой![]() и зарядом
и зарядом![]() того же знака, что и заряд шара. Найти
зависимость от времени отклонения
того же знака, что и заряд шара. Найти
зависимость от времени отклонения![]() пылинки от центра шара. Постоянная
закона Кулона
пылинки от центра шара. Постоянная
закона Кулона![]() ,
трением о стенки отверстия, сопротивлением
воздуха пренебречь.
,
трением о стенки отверстия, сопротивлением
воздуха пренебречь.
Ответ. .
.
2.8.13. Решить задачу
2.8.12 с учётом силы сопротивления воздуха,
которое пропорционально скорости
пылинки с коэффициентом
![]() .
.
Ответ. .
.
2.8.14. В диэлектрическом
шаре радиусом
![]() ,
заряженном равномерно по объёму с
плотностью
,
заряженном равномерно по объёму с
плотностью![]() ,
просверлено сквозное диаметральное
отверстие. В это отверстие попадает у
поверхности шара с нулевой скоростью
маленькая крупинка массой
,
просверлено сквозное диаметральное
отверстие. В это отверстие попадает у
поверхности шара с нулевой скоростью
маленькая крупинка массой![]() и отрицательным зарядом
и отрицательным зарядом![]() ,
покрытая сверху непроводящей оболочкой.
Найти зависимость от времени отклонения
,
покрытая сверху непроводящей оболочкой.
Найти зависимость от времени отклонения![]() крупинки от центра шара. Постоянная
закона Кулона
крупинки от центра шара. Постоянная
закона Кулона![]() ,
трением о стенки отверстия, сопротивлением
воздуха пренебречь.
,
трением о стенки отверстия, сопротивлением
воздуха пренебречь.
Ответ.![]() .
.
2.8.15. Решить задачу
2.8.14 с учётом силы сопротивления воздуха,
которое пропорционально скорости
крупинки с коэффициентом
![]() .
Считать, что
.
Считать, что![]() .
.
Ответ.
 .
.
2.8.16. На одном из
астероидов радиусом
![]() обнаружен сквозной прямолинейный канал,
параллельный оси вращения астероида и
отстоящий на расстоянии
обнаружен сквозной прямолинейный канал,
параллельный оси вращения астероида и
отстоящий на расстоянии![]() от неё. В этот канал в момент
от неё. В этот канал в момент![]() с поверхности было брошено без начальной
скорости тело. Считая плотность астероида
с поверхности было брошено без начальной
скорости тело. Считая плотность астероида![]() постоянной, найти зависимость
постоянной, найти зависимость![]() отклонения тела от наиболее глубокой
точки канала внутри астероида, если
угловая скорость вращения астероида
равна
отклонения тела от наиболее глубокой
точки канала внутри астероида, если
угловая скорость вращения астероида
равна![]() .
Гравитационная постоянная
.
Гравитационная постоянная![]() ,
трением о стенки канала, сопротивлением
атмосферного газа пренебречь.
,
трением о стенки канала, сопротивлением
атмосферного газа пренебречь.
Ответ. .
.
2.8.17. Решить задачу
2.8.16 с учётом трения скольжения между
телом и стенками канала, коэффициент
которого считать постоянным и равным
![]() .
Рассмотреть случай движения от поверхности
в сторону наиболее глубокой точки
канала; считать, что
.
Рассмотреть случай движения от поверхности
в сторону наиболее глубокой точки
канала; считать, что .
.
Ответ. .
.
2.8.18. На одном из
астероидов радиусом
![]() пробурена прямолинейная скважина до
его центра, составляющая с осью вращения
астероида угол
пробурена прямолинейная скважина до
его центра, составляющая с осью вращения
астероида угол![]() .
В эту скважину в момент
.
В эту скважину в момент![]() с поверхности было брошено без начальной
скорости тело. Считая плотность астероида
с поверхности было брошено без начальной
скорости тело. Считая плотность астероида![]() постоянной, найти зависимость
постоянной, найти зависимость![]() расстояния тела до центра астероида,
если угловая скорость вращения астероида
равна
расстояния тела до центра астероида,
если угловая скорость вращения астероида
равна![]() .
Гравитационная постоянная
.
Гравитационная постоянная![]() ,
трением о стенки канала, сопротивлением
атмосферного газа пренебречь.
,
трением о стенки канала, сопротивлением
атмосферного газа пренебречь.
Ответ. .
.
2.8.19. В диэлектрическом
шаре радиусом
![]() ,
заряженном равномерно по объёму с
плотностью
,
заряженном равномерно по объёму с
плотностью![]() ,
просверлено сквозное диаметральное
отверстие. В этом отверстии движется
непроводящий стержень длиной
,
просверлено сквозное диаметральное
отверстие. В этом отверстии движется
непроводящий стержень длиной![]() с закреплёнными на его концах зарядами
с закреплёнными на его концах зарядами![]() и
и![]() в изолированной оболочке. Общая масса
стержня с зарядами равна
в изолированной оболочке. Общая масса
стержня с зарядами равна![]() ,
в момент времени
,
в момент времени![]() второй заряд находился в центре шара,
скорость была равна нулю. Найти зависимость
от времени расстояния
второй заряд находился в центре шара,
скорость была равна нулю. Найти зависимость
от времени расстояния![]() середины стержня от центра шара до
выхода первого заряда из отверстия в
шаре. Постоянная закона Кулона
середины стержня от центра шара до
выхода первого заряда из отверстия в
шаре. Постоянная закона Кулона![]() ,
трением о стенки отверстия, сопротивлением
воздуха пренебречь.
,
трением о стенки отверстия, сопротивлением
воздуха пренебречь.
Ответ.![]() .
.
2.8.20. В диэлектрическом
шаре радиусом
![]() ,
заряженном равномерно по объёму с
плотностью
,
заряженном равномерно по объёму с
плотностью![]() ,
просверлено сквозное диаметральное
отверстие. В этом отверстии движется
непроводящий стержень длиной
,
просверлено сквозное диаметральное
отверстие. В этом отверстии движется
непроводящий стержень длиной![]() с закреплёнными на его концах зарядами
с закреплёнными на его концах зарядами![]() в изолированной оболочке. Общая масса
стержня с зарядами равна
в изолированной оболочке. Общая масса
стержня с зарядами равна![]() ,
в момент времени
,
в момент времени![]() середина стержня находилась на расстоянии
середина стержня находилась на расстоянии![]() от центра шара, скорость была равна
нулю. Найти зависимость от времени
расстояния
от центра шара, скорость была равна
нулю. Найти зависимость от времени
расстояния![]() середины стержня от центра шара до
выхода первого заряда из отверстия в
шаре. Постоянная закона Кулона
середины стержня от центра шара до
выхода первого заряда из отверстия в
шаре. Постоянная закона Кулона![]() ,
трением о стенки отверстия, сопротивлением
воздуха пренебречь.
,
трением о стенки отверстия, сопротивлением
воздуха пренебречь.
Ответ.![]() .
.
21. Стержень длиной
![]() вращается вокруг перпендикулярной ему
оси, проходящей через его середину, с
угловой скоростью
вращается вокруг перпендикулярной ему
оси, проходящей через его середину, с
угловой скоростью![]() .
По стержню скользит без трения узкое
кольцо. Найти закон изменения
.
По стержню скользит без трения узкое
кольцо. Найти закон изменения![]() расстояния от кольца до оси вращения,
если в начальный момент оно было равно
расстояния от кольца до оси вращения,
если в начальный момент оно было равно![]() ,
а скорость кольца относительно стержня
была равна нулю. Найти скорость
,
а скорость кольца относительно стержня
была равна нулю. Найти скорость![]() относительно земли, которую будет иметь
кольцо в момент соскальзывания со
стержня.
относительно земли, которую будет иметь
кольцо в момент соскальзывания со
стержня.
Ответ.![]() .
.
