2. Линейные дифференциальные уравнения
2.1. Линейные однородные дифференциальные уравнения 2-го порядка
Пусть задано
однородное дифференциальное уравнение
с постоянными коэффициентами
,
и необходимо найти его общее решение.
Приведем алгоритм решения этой задачи:
1) Ищем фундаментальные
решения уравнения в виде функций
.
Подставляя
и её производные
и
в заданное уравнение, получаем, что
числа
должны быть корнями характеристического
уравнения
.
2). Находим корни
характеристического уравнения
,
и строим фундаментальную систему
решений (ФСР):
а) если
,
− действительные различные, ФСР образуют
функции
и
;
б) если
,
− действительные и равные, ФСР образуют
функции
и
;
в) если
− комплексно сопряжённые, ФСР образуют
функции
и
.
3). Имея ФСР,
записываем общее решение заданного
уравнения
,
где
произвольные постоянные.
Если необходимо
решить задачу Коши, то есть найти функцию
,
которая является решением дифференциального
уравнения и удовлетворяет заданным
начальным условиям
,
то подставляя условия
,
в выражения
и
,
получаем систему линейных уравнений
относительно
для нахождения частного решения,
удовлетворяющего заданным начальным
условиям. Решая её, находим решение
задачи Коши.
Пример 2.1:
Решить задачу Коши:
,
.
Записать общее решение и соответствующее
заданным начальным условиям частное
решение.
Решение. 1) По
заданному дифференциальному уравнению
составляем характеристическое уравнение
.
2) Находим корни
характеристического уравнения
.
3) Имея характеристические
корни, составим ФСР
=
,
=
.
4) Имея ФСР, запишем
общее решение дифференциального
уравнения
.
5) Из общего решения находим
.
6) Используя
полученные выражения
и
,
для заданных начальных условий получим
систему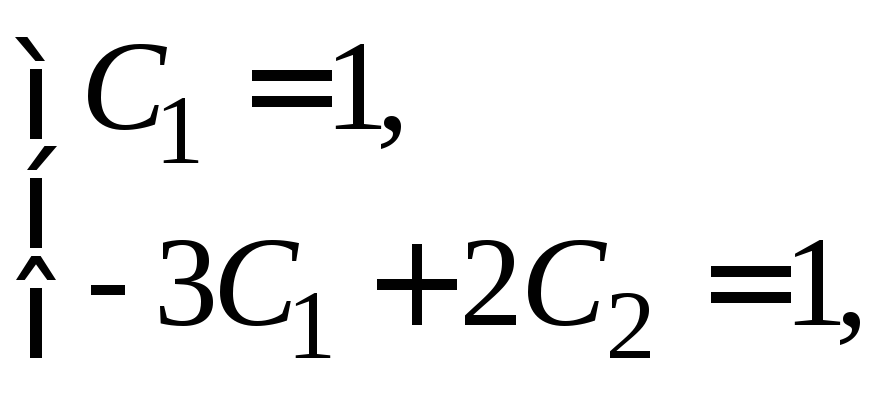
из которой
,
.
7) Запишем частное
решение (решение задачи Коши)
.
Ответ. Общее решение: , частное решение: .
Пример 2.2.
Решить задачу Коши
,
если
.
Записать общее решение и соответствующее
заданным начальным условиям частное
решение.
Решение. 1)
Составляем характеристическое уравнение
.
2) Найдём корни
характеристического уравнения
–
,
то есть имеем кратные корни.
3) Составляем ФСР
=
,
=x·
=
x·
.
4) Имея ФСР, запишем
общее решение дифференциального
уравнения
=
·
+
·
=
·
+
·
.
5) Найдем
.
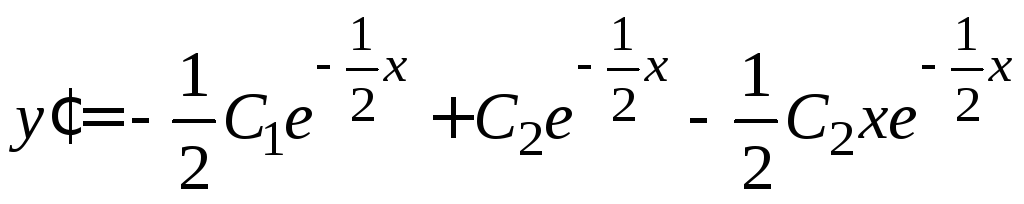6) Из системы
,
находим
,
.
6) Записываем
частное решение
,
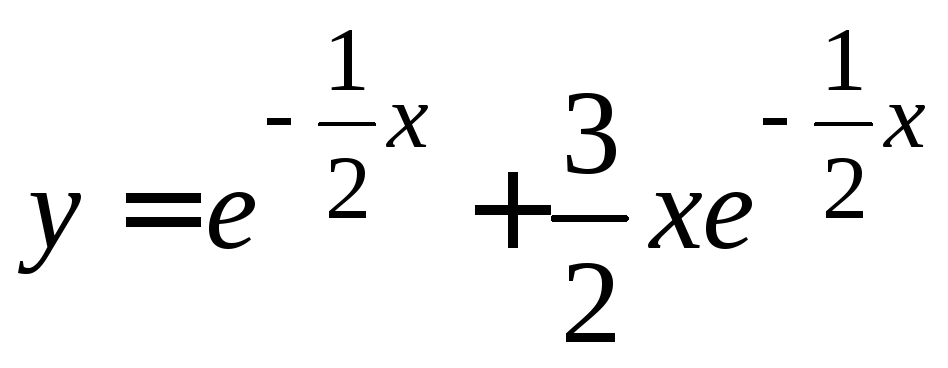удовлетворяющее начальным условиям.
Ответ. Общее решение = · + · , частное решение .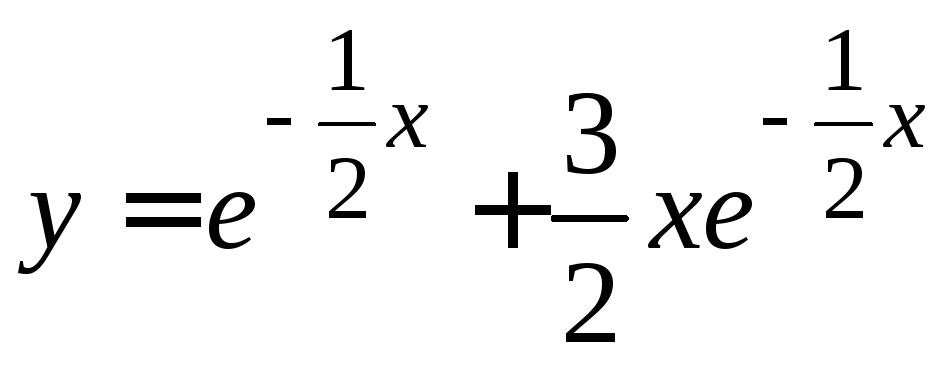
Задание 2.1. Решить задачу Коши для уравнений.
Вар. |
Уравнение |
Начальные условия |
2.1.1 |
|
. |
2.1.2. |
|
. |
2.1.3. |
; |
. |
2.1.4. |
|
|
2.1.5. |
|
. |
2.1.6. |
|
. |
2.1.7. |
|
. |
2.1.8. |
|
. |
2.1.9. |
|
. |
2.1.10. |
|
|
2.1.11. |
|
. |
2.1.12. |
|
. |
2.1.13. |
|
|
2.1.14. |
|
|
2.1.15. |
|
|
2.1.16. |
|
. |
2.1.17. |
|
. |
2.1.18. |
|
. |
2.1.19. |
|
. |
2.1.20. |
|
. |
2.1.21. |
|
. |
2.1.22. |
|
. |
2.1.23. |
|
. |
2.1.24. |
|
|
2.1.25. |
|
. |
2.1.26. |
|
. |
2.1.27. |
|
. |
2.1.28. |
|
. |
2.1.29. |
|
. |
2.1.30. |
|
. |
;
;
;
.
;
;
;
;
;
;
.
;
;
;
.
;
.
;
.
;
;
;
;
;
;
;
;
;
.
;
;
;
;
;
;