Динамика

1.14. Получите выражение, определяющее скорость центра масс системы материальных точек.

2.14. Тело массой 4 кг брошено горизонтально с некоторой начальной скоростью с высоты 45 м. Определите изменение импульса тела за время его движения, а также импульс силы, действующей на тело за это время. (Силой сопротивления воздуха пренебрегаем).

Ответ: Р = 120 (кгм)/с; Ft = Р = 120 (кгм)/с.

3.14. Горизонтально летящая пуля пробила вращающийся с частотой 10 с^1 вертикальный барабан по его диаметру, равному 1 м. Какова скорость пули внутри барабана, если расстояние по окружности между пробоинами оказалось равным 0,942 м?

Ответ: v = 33 м/с.

4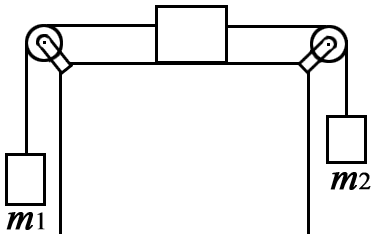.14. К крaям стола (см. рисунок) прикреплены неподвижные блоки, через которые перекинуты два шнура, привязанные к бруску, массой m = 3 кг, лежащему на столе. (Силой трения между столом и бруском пренебрегаем). К висящим концам шнуров подвешены гири, массы которых m₁ = 1,5 кг и m₂ = 2,5 кг. Определите силу натяжения каждого из шнуров. (Массой блоков и трением в блоках пренебрегаем).

Ответ: F_нат1 = m₁(g + a) = 17,1 Н; F_нат2 = m₂(g – a) = 21,5 Н.

Законы сохранения импульса и механической энергии

1.14. Какая величина остается неизменной для материальной точки, находящейся в поле фундаментальных сил? Получите эту формулу.

2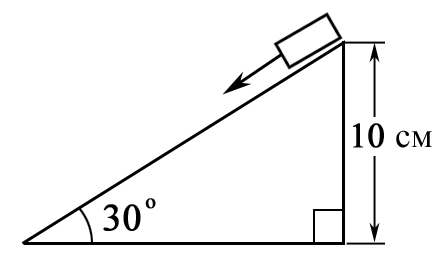.14. Брусок массой 1 кг скользит по наклонной плоскости; в начальный момент на вершине его скорость равна нулю. У основания наклонной плоскости скорость бруска равна 100 м/с. а) Какую работу совершает сила трения? б) Чему равна постоянная сила трения? в) Если покрыть наклонную плоскость масляной пленкой и уменьшить силу трения в 10 раз, то каким будет значение скорости бруска у основания наклонной плоскости?

Ответ: а) 0,48 Дж; б) F_тр = 2,4 Н; в) v = 1,365 м/с.

3.14. Для откачки нефти с глубины Н = 1000 м поставлен насос мощностью N = 10 кВт. Коэффициент полезного действия насоса  = 0,8. Какова масса m нефти, добытой за t = 10 ч работы насоса, при подаче нефти на поверхность земли со скоростью v = 0,1 м/с. Каков радиус трубы, по которой подается нефть? Считать, что уровень нефтяного пласта не понижается.

Ответ: кг; м.

4.14. Цепочка массой m = 1,0 кг и длиной l = 1,40 м висит на нити, касаясь поверхности стола своим нижним концом. После пережигания нити цепочка упала на стол. Найти полный импульс, который она передала столу.

Ответ: (кгм)/с.

ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ

1.14. Сложение скоростей в СТО.

2.14. Две нестабильные частицы движутся в К-системе отсчета по некоторой прямой в одном направлении с одинаковой скоростью v = 0,99 с. Расстояние между частицами в этой системе отсчета l = 12 м. В некоторый момент обе частицы распались одновременно в К -системе отсчета, связанной с ним. Найти: 1) промежуток времени между моментами распада обеих частиц в исходной К-системе; 2) какая частица распалась позже в К-системе.

Ответ: t₁ – t₂ = 2 мкс.

3.14. Сравните величину релятивистского и классического импульсов электрона при скорости v = (24/25) с = 0,96 с.

Ответ:  =

4.14. В лабораторной системе отсчета удаляются друг от друга две частицы с одинаковыми по модулю скоростями. Их относительная скорость U в той же системе отсчета равна 0,5 с. Определить скорости частиц.

Ответ: 0,268с.

Вариант № 15