§ 3. Плоскость и прямая в пространстве.

3.1. Даны координаты точки и уравнение плоскости:. Найти координаты точки, симметричной точкеотносительно плоскости.

Общие сведения и расчётные формулы:по представленному заданию.

В соответствии с определением симметрии точек пространства относительно плоскости нам необходимо провести через точку прямую , перпендикулярную этой плоскости и найти точку пересечения этой прямой с плоскостью. После этого из точки вдоль прямой отложить отрезок = и определить координаты точки .

Итак, пусть имеем: точку = и плоскость :. Это определяет вектор = нормали плоскости. Так как этот вектор параллелен прямой , то его можно принять в качестве направляющего вектора прямой = в каноническом уравнении прямой: ===. Одновременно запишем уравнение прямой в виде параметрических уравнений: 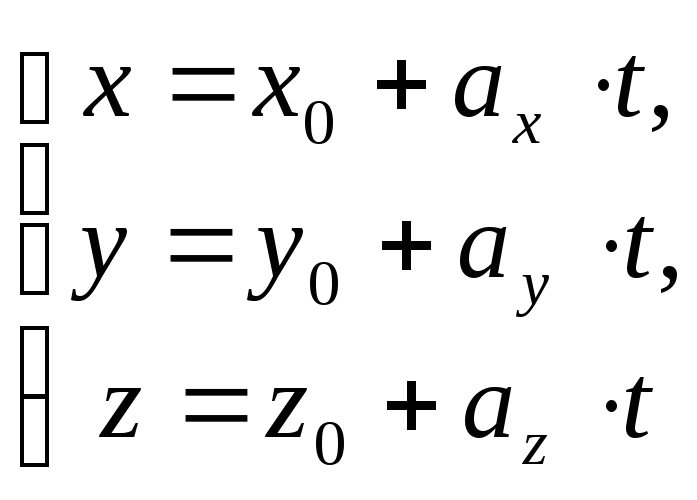. Точка пересечения прямой и плоскости может быть найдена из уравнения: → . Имея значение , находим координаты точки : . После этого нахождение координат точки не представляет труда: , или , откуда получаем: =.

Пример (и образец оформления):

Общая часть. Пусть заданы: точка=(1,0,1) и плоскость:. Найти координаты точки, симметричной точкеотносительно плоскости.

Решение:

1) Выделим вектор нормали заданной плоскости: =(4,6,4)=2(2,3,2). Примем:=(2,3,2).

2). Решим уравнение: →=.

3). Вычислим координаты точки :=.

4). Вычислим координаты точки ==2–(1,0,1)=(3,3,3).

Ответ:=(3,3,3).

Замечание: при оформлении задания использование рисунка (в карандаше, с использованием чертёжных инструментов)обязательно!

Варианты индивидуальных заданий:

Вар.	Задание:		Вар.	Задание:
1.		.	16.		.
2.		.	17.		.
3.		.	18.		.
4.		.	19.		.
5.		.	20.		.
6.		.	21.		.
7.		.	22.		.
8.		.	23.		.
9.		.	24.
10.		.	25.		.
11.		.	26.
12.		.	27.		.
13.		.	28.		.
14.		.	29.		.
15.		.	30.		.

3.2. Даны координаты точки и уравнение прямой:==. Найти координаты точки, симметричной точкеотносительно прямой:.

Общие сведения и расчётные формулы:по представленному заданию.

Всоответствии с определением симметрии точек пространства относительно прямой нам необходимо провести через точку плоскость , перпендикулярную этой прямой и найти точку пересечения прямой с плоскостью. После этого из точки вдоль прямой отложить отрезок = и определить координаты точки .

Итак, пусть имеем: точку = и прямую . Это определяет направляющий вектор прямой . Его можно принять в качестве вектора нормали плоскости : . Точка и вектор определяют плоскость. Представим уравнение прямой в параметрической форме: 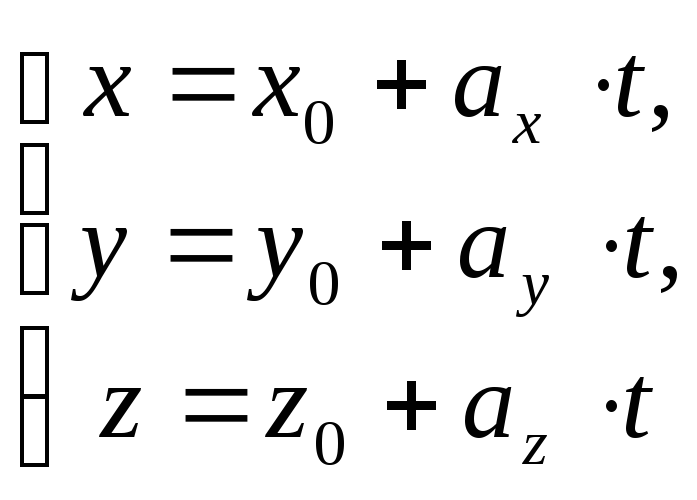. Точка пересечения прямой и плоскости может быть найдена из уравнения: → . Имея значение , находим координаты точки : . После этого нахождение координат точки не представляет труда: , или , откуда получаем: =.

Пример (и образец оформления):

Общая часть. Пусть заданы: точка=(0,-3,2) и прямая:==. Найти координаты точки, симметричной точкеотносительно прямой:.

Решение:

1) Определим направляющий вектор прямой :=(1,-1,1). Тогда==(1,-1,1).

2) Запишем уравнение плоскости :, или.

3). Представим уравнение прямой в параметрической форме:.

4). Решим уравнение: →=.

3). Вычислим координаты точки :=.

4). Вычислим координаты точки ==2–(0,-3,2)=(1,1,1).

Ответ:=(1,1,1).

Замечание: при оформлении задания использование рисунка (в карандаше, с использованием чертёжных инструментов)обязательно!

Варианты индивидуальных заданий:

Вар.	Задание:		Вар.	Задание:
1.		==.	16.		==.
2.		==.	17.		==.
3.		==.	18.		==.
4.		==.	19.		==.
5.		==.	20.		==.
6.		=.	21.		==.
7.		==.	22.		==.
8.		==.	23.		==.
9.		==.	24.		==.
10.		==	25.		==.
11.		==.	26.		==.
12.		==.	27.		==.
13.		==.	28.		==
14.		==.	29.		==.
15.		==.	30.		==.

3.3. Даны уравнения двух прямых. Установить, скрещиваются, пересекаются или параллельны эти прямые. Если прямые пересекаются или параллельны, написать уравнение содержащей их плоскости. Если прямые скрещиваются, написать уравнение плоскости, содержащей первую прямую и параллельную второй прямой.

Общие сведения и расчётные формулы:по представленному заданию.

Пусть имеем уравнения двух прямых:

: ==,

: ==.

Из уравнений прямых следуют координаты точек: =, =, и векторов: =, =.

Кратко представим названные условия задачи:

1*: Если прямые и параллельны, то ||, то есть =.

2*: Прямые и пересекаются, если смешанное произведение: =0.

3*: Прямые и скрещивающиеся, если смешанное произведение: 0.

Рассмотрим продолжение решения задачи в каждом из возможных случаев.

Случай 1*. Если прямые параллельны, то они лежат в одной плоскости. Примем: = и вычислим векторное произведение: =x=. Записываем уравнение плоскости : .

Случай 2*. Если прямые пересекаются, то они лежат в одной плоскости. Примем: = и вычислим векторное произведение: =x=. Записываем уравнение плоскости : .

Случай 3*. Если прямые скрещивающиеся, то примем: = и вычислим векторное произведение: =x=. Записываем уравнение для : .

Замечание: в каждом из возможных случаев приходим к построению одной и той же плоскости: трудоёмкость вычислений и оформления во всех вариантах одинаковы.

Пример (и образец оформления):

Общая часть. Пусть заданы прямые:==и:==. Необходимо исследовать их взаимное положение и построить оговоренную плоскость.

Решение:

1) Из уравнений прямых следует: =(1,2,3), =(0,18,0), =(2,3,1), =(3,1,2).

2) Построим вектор: =–=(0,18,0)– (1,2,3)=(-1,16,-3).

3). Так как векторы ине параллельны, то и прямыеине параллельны.

4). Вычислим смешанное произведение векторов: =, применяя любой из способов вычисления определителя 3-го порядка. В рассматриваемом примере получаем:==0 → прямыеипересекаются.

3). Примем для использования в уравнении плоскости :==(1,2,3) и вычислим векторное произведение векторови:=x====(5,-1,-7).

4). Запишем уравнение требуемой плоскости :для рассматриваемого примера:

Ответ:прямыеипересекаются; уравнение плоскости:.

Замечание: при оформлении задания использование рисунка (в карандаше, с использованием чертёжных инструментов)обязательно!

Варианты индивидуальных заданий:

Вар.	Задание:
1.	==.	==.
2.	==.	==.
3.	==.	==.
4.	==.	==.
5.	==.	==.
6.	==.	=.
7.	==.	==.
8.	==.	==.
9.	==.	==.
10.	==.	==.
11.	==.	==.
12.	==.	==.
13.	==.	==.
14.	==.	==.
15.	==.	==.
16.	==.	==.
17.	==.	==.
18.	==.	==.
19.	==.	==.
20.	==.	==.
21.	==.	==.
22.	==.	==.
23.	==.	==.
24.	==.	==.
25.	==.	==.
26.	==.	==.
27.	==.	==.
28.	==.	==.
29.	==.	==.
30.	==.	==.