Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный университет экономики, статистики и информатики (МЭСИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Исследование операций и методы оптимизации

.pdf

Скачиваний:

379

Добавлен:

05.06.2015

Размер:

2 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 2110 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

эффект. Во многих задачах полученный эффект можно использовать как ресурс для следующего шага, объединяя его с оставшимся ресурсом. Если ресурс не деньги, то средства нужно привести к единому эквиваленту с оставшимися средствами. Такая модель является развитием классической модели. Так как оставшиеся средства и доход объединяются, то можно ввести единую интегральную функцию - функцию изменения средств F(Xi) - количество оставшихся средств плюс доход после i-го шага, если вложили Xi.

I.F (Xi ) ,

II.G (Yi ) = G (k − Xi ) .

Где k -количество средств перед i-м шагом.

Выигрыш на i-м шаге зависит от того, как мы подсчитываем доход (эффект) от управления всеми ресурсами. Поставим задачу: максимизировать

доход в конце m-го шага. Тогда на всех шагах i =1,m −1 , доход = 0, Wi = 0 .

На m-м шаге выигрыш Wm = Fm (X m )+Gm (k − X m ) . Подставив эти выражения

в уравнение Беллмана, мы программируем задачу от начала к концу, если имеется начальное количество средств k0. Здесь функция траты: k′ = Fi (Xi )+Gi (k − Xi ).

Рассмотрим частный случай: когда F и G неубывающие функции. В этом случае, чем больше значение доход + средства получается в конце i-го шага, тем лучшим условием это будет для проведения (i+1)-го шага. Поэтому можно не заботиться о следующих шагах, достаточно обеспечить максимум на каждом шаге.

Таким образом, процедура оптимизации возможна в одном направлении от начала к концу, т. е. задача динамического программирования вырождается в задачу последовательной оптимизации.

max{F1 (Xi )+G1 (k0 − X1 )} = k1* ,

X2	{	F	(X		)+G		k* − X	}	= k* ,
max				2		(		2 )
		2			2		1		2

…

Удален

Отформ

Шрифт:

Удален

Отформ

Удален

Отформ

Удален

Отформ

Удален

Отформ

Удален

Отформ

Удален

Отформ

Удален

Отформ

max{Fm (Xm )+Gm (km* −1 − Xm )} = km* ,

Wmax = km* .

Рассмотрим задачу распределения ресурсов с вложением доходов в про-

Удалено:

изводство и отчислением. Это наиболее общий случай. Разделим функции

Отформа

дохода и функции траты:

Удалено:

f (Xi ), g (Yi)

Отформа

ϕ(Xi ),ψ (Yi )

Удалено:

и максимизируем суммарный отчисленный доход + оставшиеся средства по-

сле m-го шага. Введём функцию отчисления

ri (Di ); D-доход. Тогда выиг-

Удалено:

рыш на каждом шаге:

Отформа

(

i )

(

i )

Отформа

= r

+ g

−

i =

1, m −1

(

m )

+ g

(

k − X

m )

+ϕ

(

m )

+ψ

(

− X

m )

(

)

Отформа

= r

Отформа

(5.3)

W = ∑Wi

→ max

Удалено:

i=1

Удалено:

k′

=ϕ

(

i )

+ψ

(

k − X

)

+ f

(

i )

+ g

(

k − Xi

)

(

i )

+ g

(

− X

i )

−r

Уравнение Беллмана для i-го шага будет выглядеть так:

Отформа

(k )= max

r f

)+ g (k − X

) +

)+ ψ (k − X

)+ f (X

Отформа

i+1

Отформа

+g (k − X

)−r

)+ g

(k − X

)

Удалено:

, i =

1,m −1

Отформа

}

для i=m надо учесть (5.3).

Отформа

Если ri=1, то мы получаем классическую задачу.

5.5. Расширение модели задач динамического программирования

Удалено:

Учёт предыстории процесса

Удалено:

Отформа

Мы считали, что все функции, как выигрыша, так и траты, зависят от со-

стояния перед i-м шагом, т. е. не зависят от более ранних состояний. Такие

Отформа

процессы называются процессами без памяти. Но иногда при рассмотрении

Отформа

некоторых процессов требуется помнить всю историю происходящего (на-

Удалено:

пример, в задачах ремонта

и замены оборудования). Такая задача более

сложна. Введём расширенное состояние:

Отформа

Удалено:

S = (S, Si−1 , Si−2 ,K, Si−L ),

Si-L - состояние за L шагов до i-го. Тогда, считая аргументы векторами, функции не меняются ωi (S,Ui ), ϕi (S,Ui ) . Но задача становится сложней в

вычислительном аспекте. Пусть S имеет k координат и предыстория распространяется на L шагов, тогда в результате число переменных будет k×L. Вот почему подобные задачи практически можно решать если k×L≤3.

ДП для задач со многими ограничениями Пусть в задаче распределения ресурсов есть два ограничения (два ресурса).

m
W = ∑ f (Xi	)→ max,
i=1
i=1
m
∑a1i Xi ≤ b1 ,
i=1
m
∑a2i Xi ≤ b2 .
i=1

Введем два параметра состояния K1 и K2. Тогда функции условных оптимальных выигрышей и условных оптимальных управлений будут иметь по два аргумента W(K1, K2); xi(K1, K2). Уравнение Беллмана для решения такой задачи имеет вид

Wi (K1, K2 )= max{fi (Xi )+Wi+1 [K1 − a1i Xi ; K2 − a2i Xi ]}.

При этом величина Xi на каждом этапе варьируется в пределах от нуля до величины di :

di= min(K1/a1i ;K2/a2i)

Видно, что для двух ограничений, если каждая из величин K1, K2 может принимать 102 значений, то функцию Wi(K1,K2) приходится табулировать в 104 точках. Таким образом, наиболее серьезным препятствием для практического применения ДП является число параметров задачи, что заставило Р.Беллмана заявить о так называемом «проклятии многомерности». Некоторые способы понижения размерности смотри в [10].

Задача с мультипликативным критерием До сих пор мы считали, что суммарный выигрыш равен сумме выигры-

шей, полученных на i-х шагах. Но есть задачи, где общий критерий равен произведению критериальных величин на каждом шаге:

Удален

Отформ

Удален

Отформ

Удален

Отформ

русский

Отформ

Удален

Отформ

Удален

Отформ

Удален

Отформ

Удален

Отформ

Удален

Отформ

Удален

W = ∏Wi .

i=1

Вэтом случае так же можно применить уравнение Беллмана, но вместо этого можно взять функцию W ′ = lnW . Оптимальные решения будут одина-

ковы ввиду монотонности логарифмической функции. Но можно при выводе уравнения Беллмана учесть, что

Wi (S ) = max{Wi ×Wi+1 (S′)},

W = F (W1 ,W2 ,K,Wn ) = F (W1 ) F (W2 ) K F (Wn ) .

Т.о. метод ДП применим в случае, когда аргументы в критериальной функции разделяются (смотри вышеприведенное выражение)

Пример: устройство состоит из n узлов. Имеется некоторый ресурс k0, который может использоваться для повышения надёжности каждого узла. Необходимо так распределить ресурс, чтобы суммарная надёжность была максимальной. Получаем задачу

Q= ∏qi (Xi )→ max ,

i=1

где q (Xi ) - надёжность каждого узла, ∑Xi ≤ k0 .

Операции не связанные со временем Во многих задачах распределение ресурсов не связано с временными ша-

гами. Ресурс распределяется по объектам. Например, если рассмотреть распределение ресурсов между n объектами, когда на каждый объект задана функция выигрыша, то такая задача эквивалентна рассмотренной нами задаче о распределении ресурсов с резервированием в одной отрасли по n шагам. Это наиболее распространенная задача распределения ресурсов, поэтому приведем ее полное решение методом ДП.

5.6. Пример решения задачи распределения ресурсов

Рассмотрим пример. Завод получил 4 новых станка, которые необходимо распределить между тремя цехами. Известна дополнительная прибыль, которая получится в i-м цехе, если туда поставят хi станков – f(хi).

Удалено:

Отформа

Equation, П

Отформа Удалено:

Отформа

на 3 пт

Удалено: Отформа Отформа Отформа

Удалено: Отформа

Удалено: Отформа Отформа Отформа Отформа Код поля Отформа

Удалено: Отформа Удалено:

Отформа

Отформа Удалено:

Отформа Удалено: Отформа

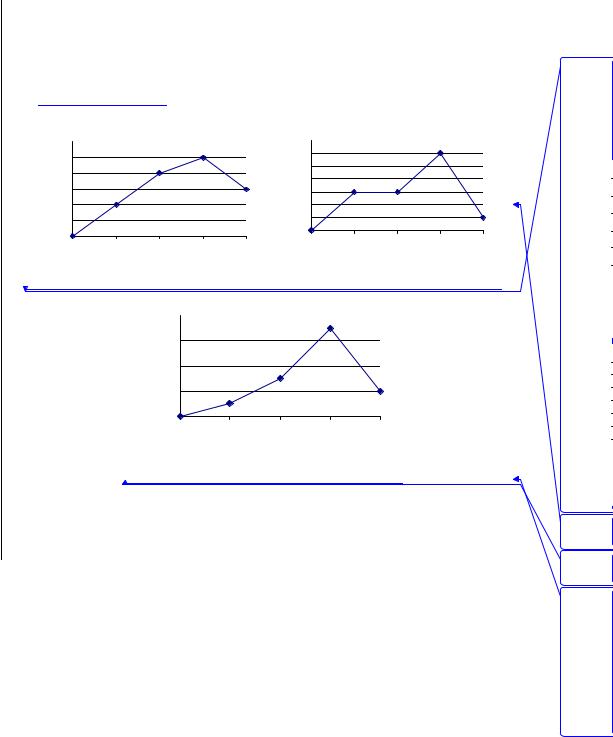
Состоянием является оставшееся (текущее) количество станков (k). Пусть мы распределяем оставшиеся k станков. Начинаем с третьего (последнего) цеха:

W (k) = max{ f (x )} .

3 x3 ≤k 123 3

W%3

	6
	5
	4				f2
f1	3				f2
	2
	1
	0
	0	1	2	3	4
			x1

7
6
5
4
3
2
1
0
0	1	2	3	4
		x2

	8
	6
f3	4
	2
	0

Рис. 30

Таблица 32

k	Х3	~	W3
k	Х3	W	W3
		3
0	0	0	0
1	0	0	1
1	1	1	1
	1	1
2	0	0	3
2	1	1	3
	2	3
3	0	0	7
3	1	1	7
	1	1

	2	3
	3	7
	0	0
4	1	1	7
4	2	3	7
	3	7
	4	2

		Таблица 33

k	х3опт	W3
0	0	0
1	1	1

Удален

ляется ос количест Пусть мы тавшиеся ем с трет цеха:¶

	6
	5
	4
f1	3
	2

		7
		6
		5
	f2	4
	f2	3
		3
		2

Отформ

интерва

Отформ

Знак Зна

Отформ

Число ко колонки Промежу

1: 35,4

колонки

Колонки ширины, колонти страниц

2	2	3
3	3	7
4	3	7

Переходим ко второму ша-

гу:

Таблица 34

	k		х2	~			W2
					W2
0		0		0		0
1		0		1		3
		1		3
2		0		3		4
		1		4
		2		3
3		0		7		7
		1		6
		2		4
		3		6
4		0		7		10
		1		10
		2		6
		3		7
		4		1
			Таблица 36
	k		Х1		~		W1
					~
					W
					1
			0		10
	4		1		9		10
	4		2		8		10
			3		8
			4		3

Так как начальное состояние известно, то для

W2	(k) = max{ f2 (x2 ) +W3 (k − x2 )} .	Отформа
W2	(k) = max{ f2 (x2 ) +W3 (k − x2 )} .	на 10 пт
	x2 ≤k
		Отформа
		Отформа
		Equation
		Удалено:

Отформа

Таблица 35 интервал П отрывать о

k	х2опт	W2
0	0	0
1	1	3
2	1	4
3	0	7
4	1	10

Переходим к первому шагу:

W1 (k) = max{ f1 (x1 ) +W2 (k − x1 )} .

x1 ≤4

первого шага не нужно перебирать оставшееся число станков, и берем k=4.

Ответ: х1*=0, х1*=4-0=4 (подставляем х1* в

табл.4), х2*=1, х2*=4-1=3 (подставляем х2* в

табл.2),

х3*=3, х3*=4-3=1.

Отформа

Equation, П в 42,55 пт

Отформа

на 10 пт

Удалено:

Отформа

Шрифт: ку

Отформа

Отступ: Пе пт, Поз.таб

42,55 пт

Отформа

Шрифт: ку

Удалено: Удалено: Удалено: Удалено: Удалено: Удалено: Удалено: Удалено: Удалено:

b!(n −1)!

5.7. Эффективность динамического программирования

Сравним по числу необходимых операций динамическое программирование с простым перебором всех вариантов для задачи

W = ∑ f (xi )− > max ,

∑ai xi < b .

Для упрощения расчёта примем a1=a2=…=an=1.

При простом переборе число возможных вариантов решений (при условии целочисленности всех переменных) равно числу способов, которыми можно разместить b одинаковых шаров внутри n урн.

Оно составляет

Cbn+b−1 = (n +b −1)! .

При n=5, b=20 имеем Ñ244 =10626 .

Удален

Отформ

выше на

Отформ

Equation 0 пт, По Поз.табу

320,35 п

Отформ

ширине, строка:

Отформ

выше на

Отформ

ниже на

Оценим число операций, требуемых для решения этой задачи методом динамического программирования.

Для вычисления Wi(k) при фиксированном k необходимо провести k+1 вычислений. Поэтому для заполнения одной таблицы Wi(k) необходимо проделать

b	(b +1)(b + 2)
∑(k +1) =		операций.
	2
k =0

Следовательно, для вычисления всех функций W1(k),…, Wn-1(k) необхо-

димо (n −1)	(b +1)(b + 2)	операций. С учётом вычисления функции Wn(b) об-
димо (n −1)	2!	операций. С учётом вычисления функции Wn(b) об-
	2!
щее число операций NΣ =			(n −1)(b +1)(b + 2)	+(b +1) =	(b +1)[(n −1)(n + 2) + 2]	.
щее число операций NΣ =			2!	+(b +1) =	2!	.
			2!		2!

При n=5, b=20 имеем N∑=945, что в 11 раз меньше, чем при простом переборе.

Удален

Отформ

Удален

Отформ

Удален

Отформ

Удален

Отформ

Удален

Отформ

6. НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

6.1. Особенности задач нелинейного программирования
Нелинейное программирование (НЛП) - это такая задача математическо-		Удалено:
		Удалено:
го программирования, в которой либо целевая функция, либо функции огра-
ничений, либо они вместе представляют собой нелинейные функции. Термин
НЛП применяется только тогда, когда все переменные X-действительные
числа. Решение задач НЛП намного сложнее решения задач ЛП, при прочих
равных условиях. Рассмотрим особенности задач НЛП, а именно то, где мо-
жет находиться оптимальное решение. Для этого будем рассматривать целе-
вую функцию двух переменных. В НЛП используют геометрический образ
целевой функции как некоторой поверхности, определённой на множестве
управляемых переменных. Вид этой поверхности можно представить, изо-
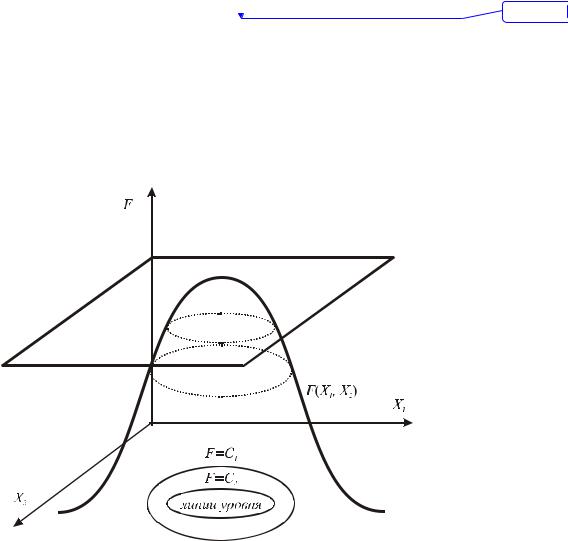
бражая в области переменных так называемые линии уровня, (рисунок 31)

Рис. 31

Особенности задач НЛП проиллюстрируем графически на примере задачи:

F = (x1 −1/2)2 +(x2 −1)2 → min,x1x2 ≤ a ,

x1 + x2 ≥ b,

0 ≤ x1 ≤ 3; 0 ≤ x2 ≤ 3.

Изобразим графически область допустимых решений (ОДР) и найдем решение для различных значений a и b. Очевидно, что оптимальное решение будет находиться в точке, где линия уровня имеет самую малую величину в области допустимых решений (ОДР). Это можно представить как «последнее касание» линии уровня ОДР по мере уменьшения этого уровня. Линии уровня в этой задаче представляют собой концентрические окружности, а FÆ min соответствует уменьшению их радиуса.

1)a =2, b=2 (рис. 32а);

2)a =1/2, b=2 (рис. 32б).

а)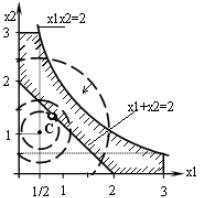 б)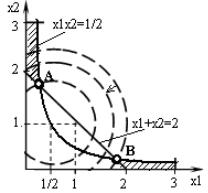 Рис. 32

Решение задачи на рис. 32а находится в точке С, где линия наименьшего уровня целевой функции касается прямой x1 + x2 = 2 . Координаты оптималь-

ного решения x1 = 34 ; x 2 = 54 можно найти из простых геометрических сооб-

ражений.

Решение задачи на рис. 32б качественно отличается от первого случая, так как здесь получаются две несвязанных ОДР, дающих две экстремальные точки А и В, являющиеся точками пересечения линий

x1 x2 =1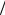2 и x1 + x2 = 2 .

Точка B является точкой локального минимума, а точка А точкой глобального минимума. Ее координаты найдем, решив систему уравнений:

x x =1 2,
1	2	= 2,
x1	+ x2	= 2,
xA	=1−	2	≈ 0,3,	xA =1+	2	≈1,7 .
xA	=1−		≈ 0,3,	xA =1+		≈1,7 .
1		2		2	2
		2			2
	3)	а=2, b=1.				Рис. 33

Решение на рис. 33 находится в точке Д, являющейся координатами центра концентрических окружностей (линий уровня целевой функции).

Из приведенных примеров ясно, что решение задачи НЛП может находиться как внутри ОДР (рис. 33), на одной из границ в произвольной точке (рис. 32а), так и в вершинах ОДР, являющихся точками пересечений функций ограничений (рис. 32б), причем может получиться несколько экстремальных точек.

Графическое изображение ОДР и линий уровня F(x) позволяет решать задачи НЛП с двумя переменными.

6.2.Прямые методы одномерной оптимизации нелинейных функций без ограничений

Пусть на множестве U R определена функция F(X). Под минимизацией функции F(X) на множестве U будем понимать решение следующей задачи: найти хотя бы одну точку минимума x* и минимум F*=F(X*) этой функции на множестве U.

Многие приближенные методы минимизации применимы только тогда, когда любой локальный минимум F(X) является одновременно и глобальным. Одним из классов функций, удовлетворяющих этому условию, является класс унимодальных функций.

Функция F(X) называется унимодальной на отрезке [a;b], если она непрерывна на [a;b] и существуют числа α и β, a≤α≤β≤b, такие, что:

1) если a<α, то на отрезке [a; α] F(X) монотонно убывает; 2) если β<b, то на отрезке [β;b] F(X) монотонно возрастает;

3) при x [α;β] F(X ) = F * = min F (X ) .

[a;b]

Отформа

Отступ: Сл строка: 14 нумерован + Стиль ну … + Начат Выравнива Выровнять Табуляция Отступ: 36 Поз.табуля Выровнять табуляции

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 2110 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.06.2015501.08 Кб77ИСиТ Тема 8 2011.docx
#
05.06.201576.98 Кб13ИСиТ Тема 9 2011.docx
#
05.06.2015120.32 Кб26исп1Диплом Егорова Полина.doc
#
22.11.20182.27 Mб4Исследование когнитивных представлений о лидерс....doc
#
22.11.2018450.56 Кб6Исследование когнитивных представлений о лидерс....docx
#
05.06.20152 Mб379Исследование операций и методы оптимизации.pdf
#
05.11.20184.61 Mб4исследование функций.doc
#
05.06.2015264.05 Кб147Истор российского предпринимательства.docx
#
05.06.201562.46 Кб11историческая школа.doc
#
26.08.2019182.78 Кб2История (Федосова).doc
#
08.11.2018254.46 Кб11История государства и права зарубежных стран 3.doc