
- •21 Коэффициент детерминации: интерпретация и вычисления по результатам корреляционного и регрессионного анализа
- •22. Какие задачи в регрессионном анализе решаются с помощью t- критерия Стьюдента
- •23. Какие задачи в регрессионном анализе решаются с помощью f-распредления Фишера-Снедекора
- •25 . Что характеризуют элементы ковариационной матрицы коэффициентов в классической линейной модели множественной регрессии и как ее анализировать
- •30.Какие способы устранения мультиколлинеарности существуют?
- •46.Содержательная интерпретация коэффициентов степенной регрессионной модели
- •47.Содержательная интерпретация коэффициентов полулогарифмических и логарифмических моделей регрессии
- •48. Коэффициенты эластичности и их использование в эконометрическом анализе
- •49. В чем отличие модели логистической регрессии от модели линейной регрессии
- •50.Формы записи коэффициентов логистической регрессии и их содержательная интерпретация Подбор параметров
- •51)Как рассчитывается прогноз наступления события в модели логистической регрессии
- •52)Классификация на основе модели логистической регрессии, проблема специфичности и общности
- •53)Понятие модели бинарного выбора
- •56) Основные виды систем одновременных эконометрических уравнений
- •57) Структурная и приведенная форма системы одновременных эконометрических уравнений
- •58) Проблема идентификации при оценке параметров системы одновременных эконометрических уравнений
- •59) В чем суть косвенного метода наименьших квадратов, когда он используется
- •60) В чем суть двухшагового метода наименьших квадратов, когда он используется
46.Содержательная интерпретация коэффициентов степенной регрессионной модели
К
классу степенных функций относятся
кривые спроса и предложения, кривые
Энгеля. Если степенная функция отражает
зависимость объема выпуска продукции
y
от использования ресурса x
( в которой 0<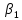 <1),
то она называется производственной
функцией. Например, производственная
функция Кобба-Дугласа связывает объем
производства Y
с затратами капитала K
и затратами труда L:
Y=A
<1),
то она называется производственной
функцией. Например, производственная
функция Кобба-Дугласа связывает объем
производства Y
с затратами капитала K
и затратами труда L:
Y=A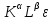 .
Автономная зависимость от времени
выражена в коэффициенте научно-технического
прогресса А. Показатели
.
Автономная зависимость от времени
выражена в коэффициенте научно-технического
прогресса А. Показатели
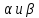 являются коэффициентами частной
эластичности объема производстваY
соответственно по затратам капитала K
и труда L.
Это означает, что при увеличении затрат
капитала(труда) на 1% объем производства
увеличивается на
являются коэффициентами частной
эластичности объема производстваY
соответственно по затратам капитала K
и труда L.
Это означает, что при увеличении затрат
капитала(труда) на 1% объем производства
увеличивается на
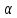 %(
%(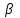 ).
).
Сумма
коэффициентов является важным
экономическим показателем, который
носит название отдача
от масштаба. При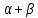 >1 – возрастающая отдача от масштаба(увеличение
объема выпуска больше увеличения затрат
ресурсов). При
>1 – возрастающая отдача от масштаба(увеличение
объема выпуска больше увеличения затрат
ресурсов). При
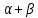 <1- убывающая отдача от масштаба
(увеличение
объема выпуска меньше увеличения затрат
ресурсов).
При
<1- убывающая отдача от масштаба
(увеличение
объема выпуска меньше увеличения затрат
ресурсов).
При
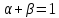 говорят о постоянной отдаче от масштаба(
во сколько раз увеличиваются затраты
ресурсов, во столько же раз увеличивается
выпуск)
говорят о постоянной отдаче от масштаба(
во сколько раз увеличиваются затраты
ресурсов, во столько же раз увеличивается
выпуск)
47.Содержательная интерпретация коэффициентов полулогарифмических и логарифмических моделей регрессии
Полулогарифмическая модель:
Модель
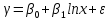 используется обычно в тех случаях, когда
необходимо исследовать, как процентное
изменение независимой переменной влияет
на абсолютное изменение зависимой
переменной. Так, например, если y=ВНП,
а x=М,
получим ВНП=
используется обычно в тех случаях, когда
необходимо исследовать, как процентное
изменение независимой переменной влияет
на абсолютное изменение зависимой
переменной. Так, например, если y=ВНП,
а x=М,
получим ВНП=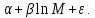 Из
данной формулы следует, что увеличение
предложения денег М га 1% ведет к росту
среднего значения ВНП на 0,01
Из
данной формулы следует, что увеличение
предложения денег М га 1% ведет к росту
среднего значения ВНП на 0,01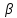

48. Коэффициенты эластичности и их использование в эконометрическом анализе
|
Коэффициент эластичности представляет собой показатель силы связи фактора xг с результатом у, показывающий, на сколько процентов изменится значение у при изменении значения фактора на 1 %. Коэффициент эластичности (Э) рассчитывается как относительное изменение у на единицу относительного изменения x:
Различают
обобщающие
(средние) и точечные коэффициенты
эластичности.
Обобщающий коэффициент эластичности
рассчитывается для среднего значения
Таблица 1
Только для степенных функций y=a·xbкоэффициент эластичности представляет собой постоянную независящую отхвеличину (равную в данном случае параметруb). Именно поэтому степенные функции широко используются в эконометрических исследованиях. Параметрbв таких функциях имеет четкую экономическую интерпретацию – он показывает процентное изменение результата при увеличении фактора на1%. Так, если зависимость спросауот ценpхарактеризуется уравнением вида: y=200p-1,5, то, следовательно, с увеличением цен на1%спрос снижается в среднем на1,5%. Несмотря на широкое использование в эконометрике коэффициентов эластичности, возможны случаи, когда их расчет экономического смысла не имеет. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения значений в процентах. Например, бессмысленно определять, на сколько процентов изменится заработная плата с ростом возраста рабочего на1%. В такой ситуации степенная функция, даже если она оказывается наилучшей по формальным соображениям (исходя из наибольшего значенияR2), не может быть экономически интерпретирована. |
Или лучше это
http://www.e-reading-lib.org/chapter.php/1002275/48/Yakovleva_Angelina_-_Otvety_na_ekzamenacionnye_bilety_po_ekonometrike.html
Коэффициенты эластичности наряду с индексами корреляции и детерминации для нелинейных форм связи применяются для характеристики зависимости между результативной переменной и факторными переменными. С помощью коэффициентов эластичности можно оценить степень зависимости между переменными х и у.
Коэффициент эластичности показывает, на сколько процентов изменится величина результативной переменной у, если величина факторной переменной изменится на 1 %.
В общем случае коэффициент эластичности рассчитывается по формуле:
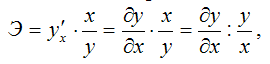
![]() –первая
производная результативной переменной
у по факторной переменной x.
–первая
производная результативной переменной
у по факторной переменной x.
Коэффициенты эластичности могут быть рассчитаны как средние и точечные коэффициенты.
Средний
коэффициент эластичности
характеризует, на сколько процентов
изменится результативная переменная
у
относительно своего среднего уровня
![]() если
факторная переменнаях
изменится на 1 % относительного своего
среднего уровня
если
факторная переменнаях
изменится на 1 % относительного своего
среднего уровня
![]() .
Общая формула для расчёта коэффициента
эластичности для среднего значения
.
Общая формула для расчёта коэффициента
эластичности для среднего значения![]()
факторной переменной х:
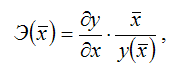
![]() –значение
функции у при среднем значении факторной
переменной х.
Для
каждой из разновидностей нелинейных
функций средние коэффициенты эластичности
рассчитываются по индивидуальным
формулам.
Для линейной
функции вида:
yi=,
средний коэффициент эластичности
определяется по формуле:
–значение
функции у при среднем значении факторной
переменной х.
Для
каждой из разновидностей нелинейных
функций средние коэффициенты эластичности
рассчитываются по индивидуальным
формулам.
Для линейной
функции вида:
yi=,
средний коэффициент эластичности
определяется по формуле:
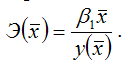
Для полиномиальной функции второго порядка (параболической функции) вида:
![]()
средний коэффициент эластичности определяется по формуле:
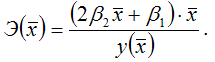
Для
показательной
функции
вида:
![]()
средний коэффициент эластичности определяется по формуле:
![]()
Для
степенной функции вида:
![]()
средний коэффициент эластичности определяется по формуле:
![]()
Точечные коэффициенты эластичности характеризуются тем, что эластичность функции зависит от заданного значения факторной переменной х1.
Точечный коэффициент эластичности характеризует, на сколько процентов изменится результативная переменная у относительно своего значения в точке х1, если факторная переменная изменится на 1 % относительно заданного уровня х1.
Общая формула для расчёта коэффициента эластичности для заданного значения х1факторной переменной х:
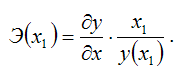
Для каждой из разновидностей нелинейных функций средние коэффициенты эластичности рассчитываются по индивидуальным формулам.
Для
линейной функции вида: yi=,
точечный коэффициент эластичности
определяется по формуле:
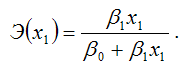
Для
показательной функции:
![]()
Для
степенной функции:
![]()
Чаще всего коэффициенты эластичности применяются в анализе производственных функций. Однако их расчёт не всегда имеет смысл, потому что в некоторых случаях интерпретация факторных переменных в процентном отношении невозможна или бессмысленна.
