5.2. Линейная зависимость и независимость векторов

Важную роль в дальнейшем изложении будет играть понятие линейной зависимости и независимости векторов.

Определение.ПустьR– векторное пространство. Векторыназываются линейно зависимыми, если существуют такие числа, не равные одновременно нулю, что

(5.2.1)

Векторы, не являющиеся линейно зависимыми называются линейно независимыми. Другими словами, векторы называются линейно независимыми, если равенство (5.2.1) выполняется, тогда и только тогда, когда,,…,.

Пусть векторы линейно зависимы, т.е. пусть в соотношении (5.2.1) хотя бы один из коэффициентов, например,отличен от нуля. Тогда

и, разделив на и положив

,,…,,

получим

(5.2.2)

Если вектор выражается через векторыв виде (5.2.2), то говорят, чтоесть линейная комбинации векторов.

Таким образом, если векторы линейно зависимы, то хотя бы один из них является линейной комбинацией остальных. Верно и обратное утверждение: векторы, один из которых есть линейная комбинация остальных, линейно зависимы. На прямой любые два вектора пропорциональны, т.е. линейно зависимы. На плоскости можно найти два линейно независимых вектора, но всякие три вектора линейно зависимы. ЕслиR– совокупность векторов трехмерного пространства, то три линейно независимых вектора вRможно найти, но всякие четыре вектора линейно зависимы. Из приведенных примеров мы видим, что максимальное число линейно независимых векторов на прямой, плоскости, в трехмерном пространстве совпадает с тем, что в аналитической геометрии принято называть размерностью прямой, плоскости, пространства.

Введем определение размерности векторного пространства.

Определение.Векторное пространствоRназываетсяn-мерным, если в нем существуетnлинейно независимых векторов, но больше чемnлинейно независимых векторов оно не содержит. Векторное пространство размерностиnобозначаетсяR_n.

Если в пространстве R можно найти любое число линейно независимых векторов, то R называется бесконечномерным. Бесконечномерные пространства составляют предмет специального изучения. В линейной алгебре изучаются только конечномерные пространства.

5.3. Базис векторного пространства

Определение.Совокупностьnлинейно независимых векторовпространстваR_nназывается его базисом. Согласно определениюnмерного векторного пространстваR_nв нем существуетnлинейно независимых векторов, т.е. существует базис.

Теорема.Каждый векторвекторного пространства можно представить, и притом единственным образом как линейную комбинацию векторов базиса.

Доказательство.Пусть, векторыобразуют базис вR_n. Присоединим к ним произвольный векторизR_n. Так как каждая система из (n+1) векторов пространстваR_nлинейно зависима, то линейно зависима и система, т.е. существуют такие не равные одновременно нулю числачто

(5.3.1)

При этом , так как иначе из формулы (5.3.1) следовала бы линейная зависимость векторов. Выражая из (5.3.1) вектор, получим

Полагая ,, будем иметь

Данное представление вектора через векторыединственно, так как еслии, то. Ввиду линейной независимости векторов,, откуда.

Таким образом, если в n-мерном векторном пространствеR_nзадан базис, то, используя выражениеможно установить взаимно однозначное соответствие между векторами этого пространства и упорядоченными последовательностями изnчисел. Числабудем называть координатами векторав базисеи будем писать. Из приведенной теоремы следует, что два вектораивR_nравны тогда и только тогда, когда их координаты в базисеравны, т.е. когда.

Рассмотрим действия над векторами в координатной форме.

Пусть в пространстве R_nзадан базис. Так как любой вектор изR_nможно представить, и притом единственным образом, в виде линейной комбинации базисных векторов, т.е.

,

то на основании аксиом, которым удовлетворяют операции сложения и умножения на число, имеем

,

.

Отсюда следует, что если векторы пространства R_n, заданы своими координатами относительно некоторого базиса, то при сложении векторов или умножении их на числокоординаты векторов соответственно складываются или умножаются на. Таким образом,

,

и если

где

,

,

…………………….

,

,

то

,

,

………………………………..

.

У нулевого вектора все координата равны нулю, так как из равенстваввиду линейной независимости векторов, вытекает, что. Вектор, противоположный кравентак как.

Примеры.

1. Для случая трехмерного пространства R₃определение координат вектора совпадает с имеющимся в аналитической геометрии определением координат вектора в некоторой системе координат.

2. Пусть R_n– пространство, векторами которого являются упорядоченные системыизnчисел.

Очевидно, что nвекторов

,

,

………………..

,

образуют базис этого пространства. Найдем координаты векторав этом базисе:

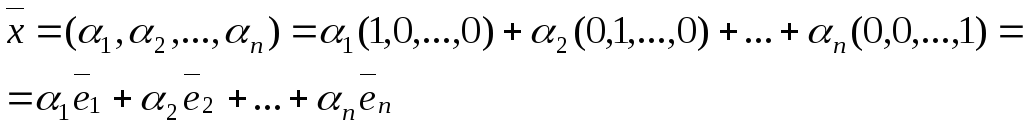
Отсюда следует, что числа можно рассматривать как координаты векторав базисепространства.

3. – пространство, векторами которого являются многочлены степени меньшей либо равной (). Простейшим базисом является совокупность векторов. Тогда координатами многочленав этом базисе являются его коэффициенты. Выберем другой базис:. Каждый многочлен по формуле Тейлора может быть представлен в виде. Таким образом, в этом базисеP(t)имеет координаты.