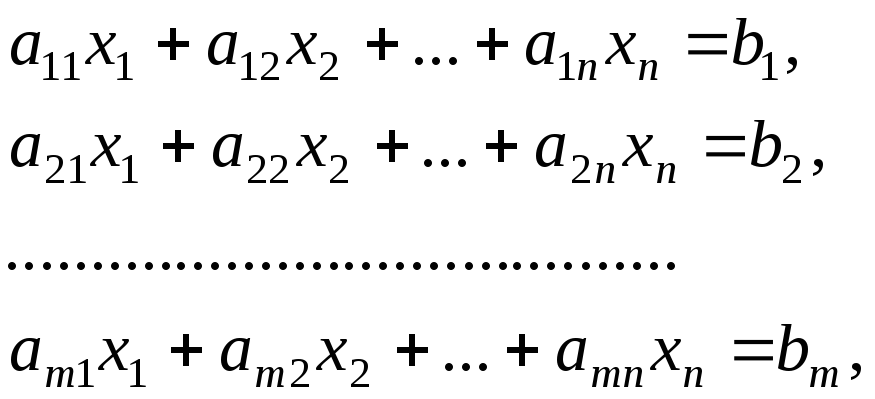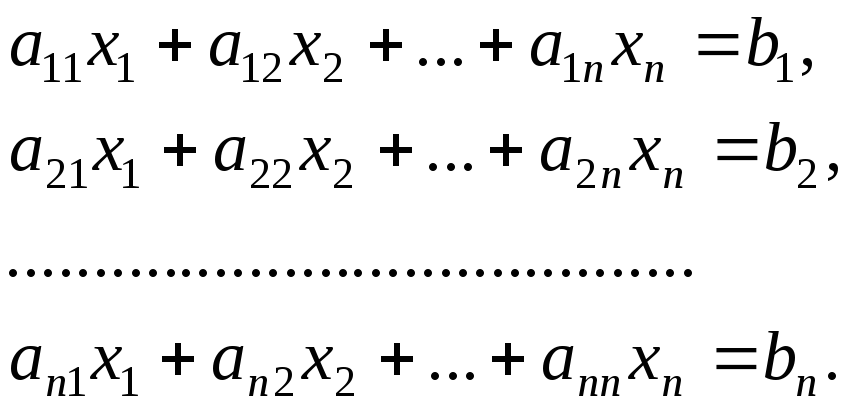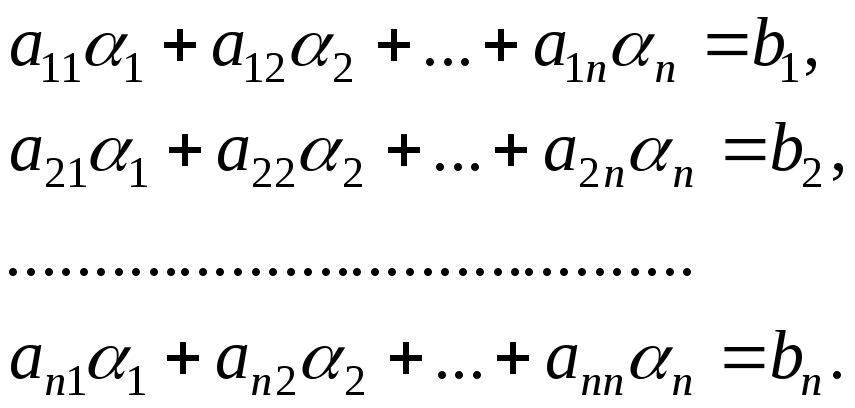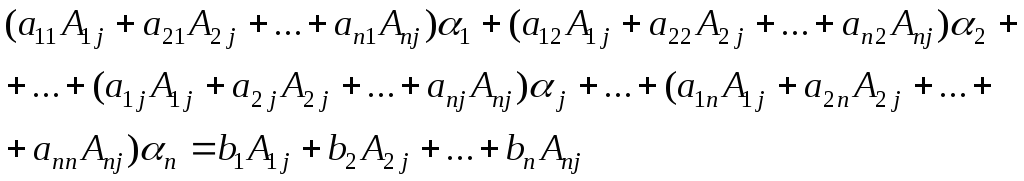3.5. Задания для самостоятельной работы по главе 3
3.1. Найти обратную матрицу
.
3.2. Найти обратную матрицу порядка n
.
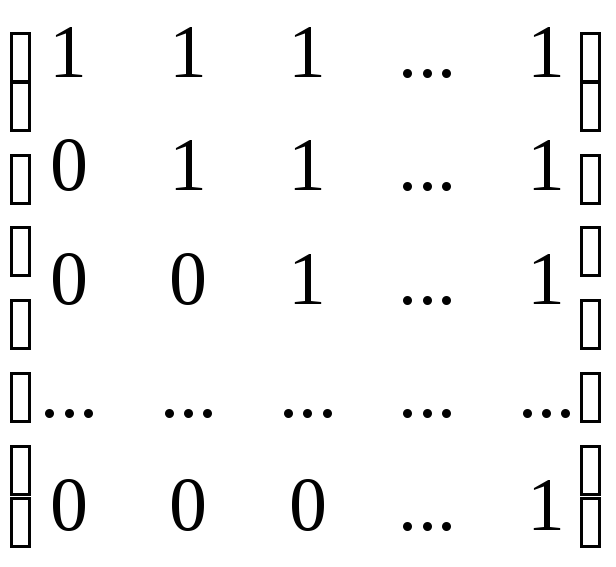3.3. Найти обратную матрицу порядка n
.
3.4. Найти обратную матрицу порядка n
.
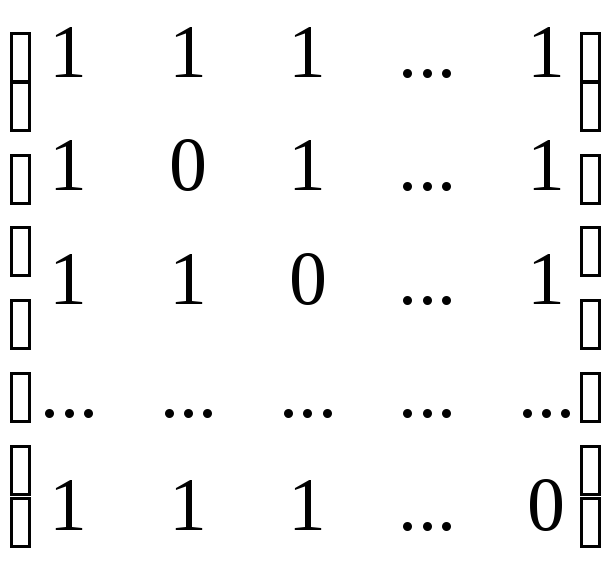3.5. Найти обратную матрицу
.
3.6. Найти обратную матрицу порядка (n+1)
.
3.7. Найти обратную матрицу порядка n
.
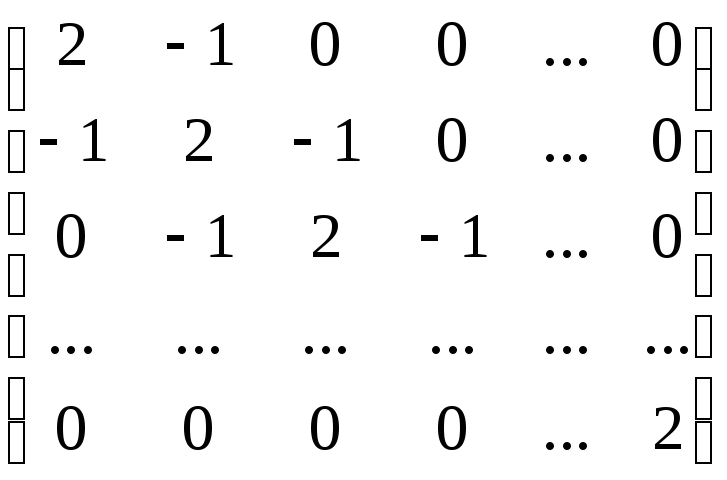3.8.
Как изменится обратная матрица
,
если в данной матрице
:
а) переставить i-ую и j-ую строки?
б) i-ую строку умножить на число с, не равное нулю?
в) к i-ой строке прибавить j-ую, умноженную на число с, или совершить аналогичное преобразование столбцов?
3.9.
Найти матрицу
,
обратную для матрицы
,
где
и
– единичные матрицы соответственно
порядковk
и l,
U
– произвольная матрица порядка
,
а все остальные элементы равны нулю.
3.10. Показать, что операция транспонирования матрицы обладает свойствами:
а)
;
б)
;
в)
;
г)
,
где с – число, а А и В – матрицы.
3.11.
Доказать, что если А
и В
– симметрические квадратные матрицы
одинакового порядка, то матрица
является симметрической.
3.12.
Показать, что для любой матрицы В
матрица
является симметрической.
3.13.
Квадратная матрица
порядкаn
называется
ортогональной, если
,
гдеЕ –
единичная матрица. Показать, что для
ортогональности квадратной матрицы А
необходимо
и достаточно любое из следующих условий:
а) столбцы А образуют ортонормированную систему, т.е.
,
где
– символ Кронекера, обозначающий 1 приi=j
и 0 при
;
б) строки А образуют ортонормированную систему, т.е.
.
3.14. Доказать, что ранг суммы двух матриц не больше суммы их рангов.
3.15. Доказать, что если ранг матрицы А равен r, то минор d, стоящий на пересечении любых r линейно независимых строк и r линейно независимых столбцов этой матрицы, отличен от нуля.
Глава 4. Решение системы линейных уравнений
4.1. Система линейных уравнений
Системой m линейных уравнений с n неизвестными называется система m алгебраических уравнений первой степени вида
|
|
(4.1.1) |
где
– неизвестные, подлежащие определению;
–числа,
называемые коэффициентами при неизвестных;
–числа,
называемые свободными членами.
Решением
системы уравнений (4.1.1) называется
совокупность n
чисел
таких, что если в каждое уравнение
системы вместо неизвестных подставить
эти числа (
вместо
,
вместо
вместо
),
то все уравнения обратятся в тождества.
Если система линейных уравнений (4.1.1) имеет хотя бы одно решение, то она называется совместной. В противном случае система называется несовместной.
Совместная система, имеющая единственное решение, называется определенной, а система, имеющая более одного решения – неопределенной.
Две системы линейных уравнений называются эквивалентными, если любое решение каждой из них является одновременно решением и другой системы.
Две произвольные несовместные системы считаются эквивалентными.
Системе
линейных уравнений (4.1.1) поставим в
соответствие матрицу
и расширенную матрицу
,
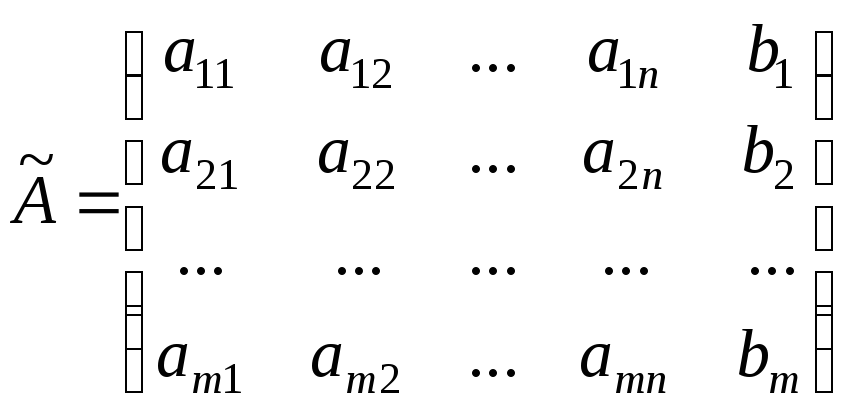полученную присоединением к матрице А столбца свободных членов.
4.2. Методы решения системы n линейных уравнений с n неизвестными
Рассмотрим систему n линейных уравнений с n неизвестными
|
|
(4.2.1) |
Определитель |A| матрицыАназывается определителем системы (4.2.1).
Теорема Крамера.Если определитель |A| системы (4.2.1) отличен от нуля, то система совместна и имеет единственное решение.
Доказательство.Пусть система
(4.2.1) совместна и
– одно из ее решений. Тогда получимnтождеств:
|
|
(4.2.2) |
Умножим обе части первого из равенств
(4.2.2) на алгебраическое дополнение
,
обе части второго равенства умножим на
алгебраическое дополнение
и т.д. и обе частиn-ого
равенства – на
.
Складывая левые и правые части полученных
выражений, придем к следующему равенству:
|
|
(4.2.3) |
Коэффициент при
равен определителю |A|
системы (4.2.1), коэффициент при
равен нулю, а правая часть равенства
(4.2.3) является определителем, полученным
из определителя |A|
путем замены j-го
столбца столбцом свободных членов.
Обозначим данный определитель через
Тогда равенство (4.2.3) примет вид:
,
откуда
|
|
(4.2.4) |
Из формулы (4.2.4) следует, что если система (4.2.1) совместна, то она обладает единственным решением.
Формулы (4.2.4) называются формулами Крамера.
Непосредственной подстановкой значений
,
во все уравнения системы убедимся в
том, что они образуют ее решение:
.
При
,
при
,
.
Таким образом, получим
.
Теорема доказана.
Пример.Решить систему линейных уравнений методом Крамера:
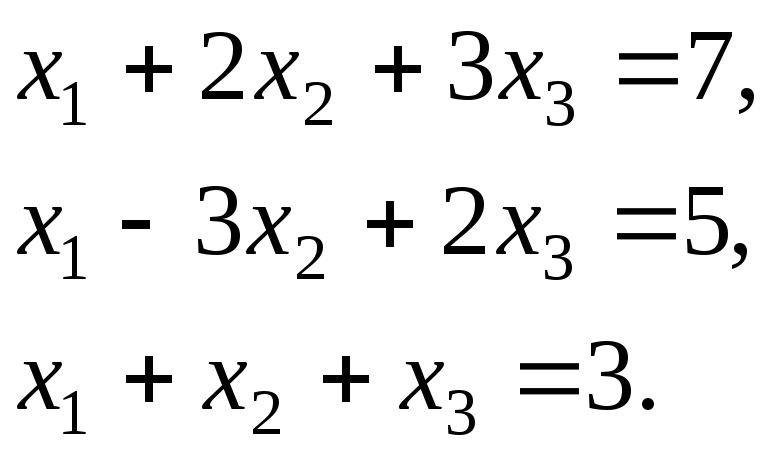
Решение.Вычислим определитель
:
,
,
,
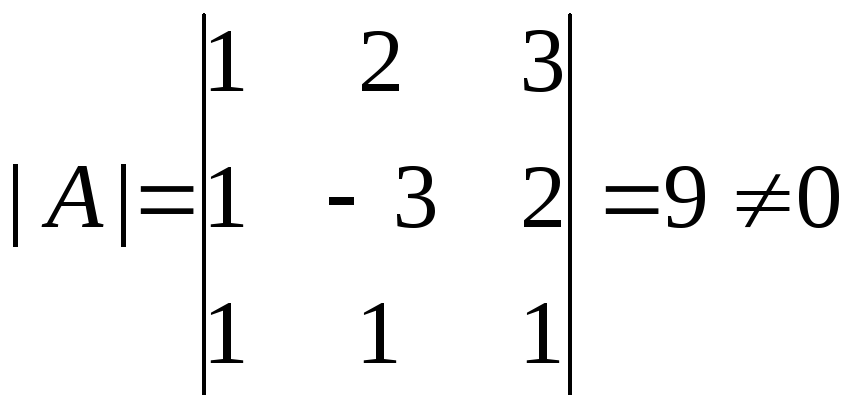
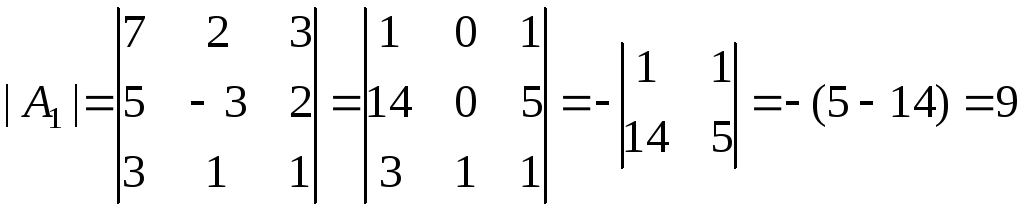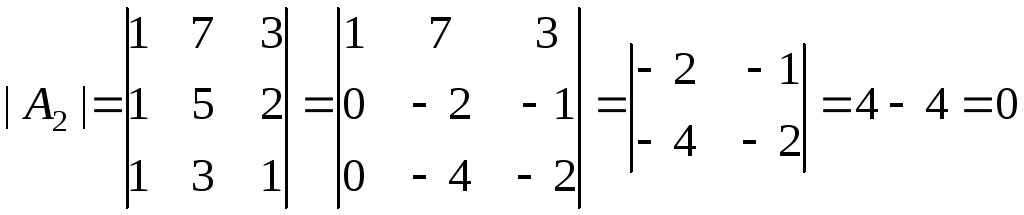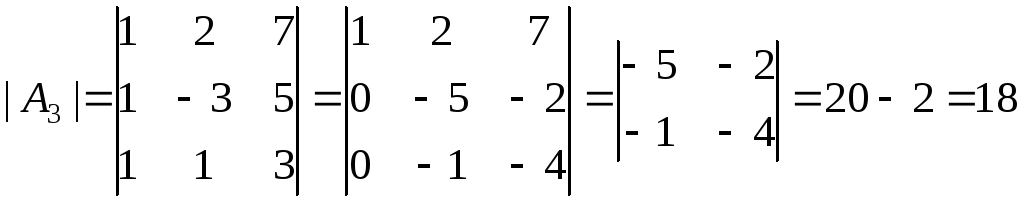откуда
Решение системы линейных уравнений с определителем |A|, отличным от нуля, можно найти с помощью обратной матрицы. Для этого запишем систему (4.2.1) в виде матричного уравнения
|
АХ=В |
(4.2.5) |
где
.
Решение матричного уравнения (4.2.5) имеет вид
|
|
(4.2.6) |
Пример.Решить систему линейных уравнений с помощью обратной матрицы
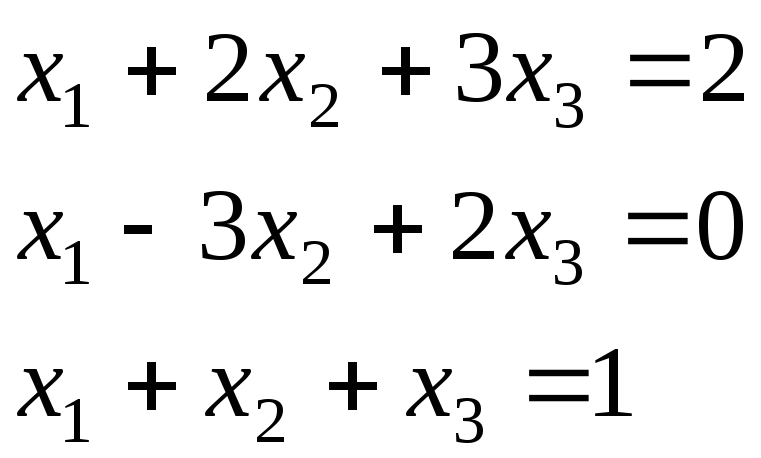
Решение.Вычислим для матрицы
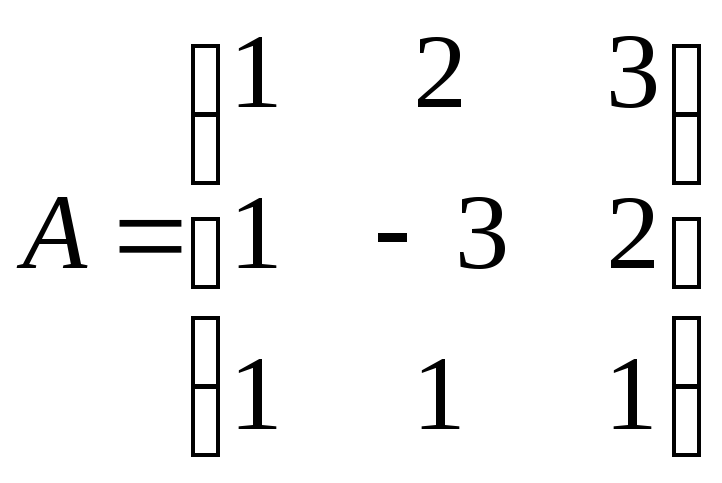
ее обратную матрицу
.
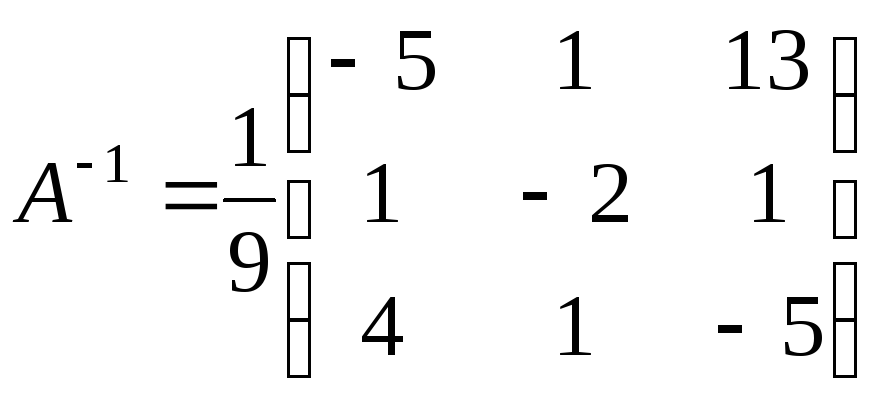Определим неизвестную матрицу-столбец Х:
,
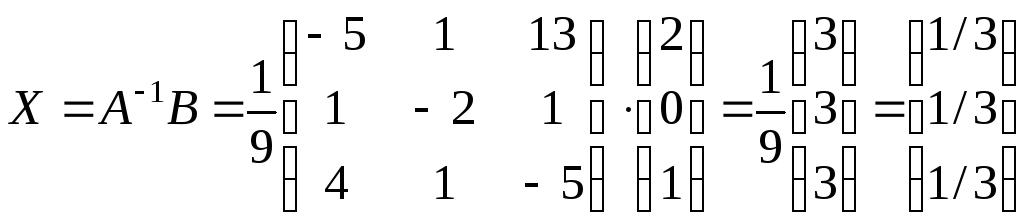откуда
Формулы Крамера
(4.2.4) могут быть получены из выражения
(4.2.6). Действительно, запишем матричное
равенство
в развернутом виде:
.
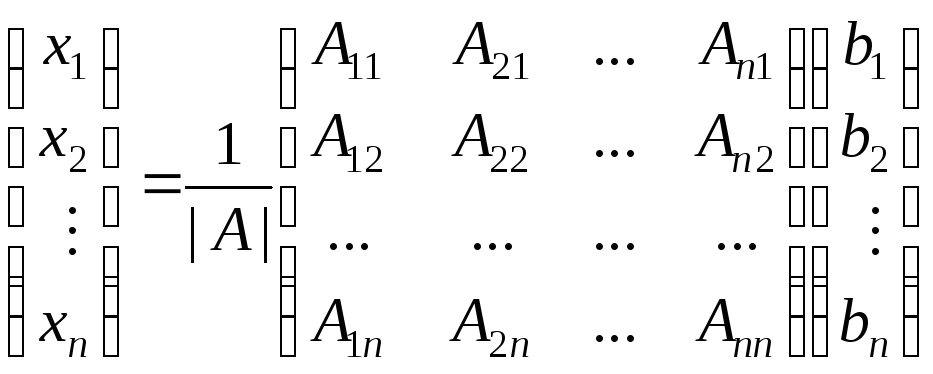Из полученного выражения непосредственно следуют формулы Крамера:
.