2.3. Задачи и упражнения

2.1. Из генеральной совокупности (y,x⁽¹⁾, ...,x^(p)), гдеyимеет нормальный закон распределения с условным математическим ожиданиеми дисперсией², взята случайная выборка объемомn, и пусть (y_i,x_i⁽¹⁾, ...,x_i^(p)) - результатi-го наблюдения (i=1, 2, ...,n). Определить: а) математическое ожидание МНК-оценкивектора; б) ковариационную матрицу МНК-оценкивектора; в) математическое ожидание оценки.

2.2.По условию задачи 2.1 найти математическое ожидание суммы квадратов отклонений, обусловленных регрессией, т.е.EQ_R, где

.

2.3.По условию задачи 2.1 определить математическое ожидание суммы квадратов отклонений, обусловленных остаточной вариацией относительно линий регрессии, т.е.EQ_ост, где

.

2.4.Доказать, что при выполнении гипотезы Н₀:=0 статистика

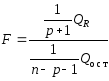
имеет F-распределение с числами степеней свободы ₁=p+1 и₂=n-p-1.

2.5.Доказать, что при выполнении гипотезы Н₀:_j=0 статистикаимеет t-распределение с числом степеней свободы=n-p-1.

2.6.На основании данных (табл.2.3) о зависимости усушки кормового хлеба (y) от продолжительности хранения (x) найти точечную оценку условного математического ожидания в предположении, что генеральное уравнение регрессии - линейное.

Таблица 2.3.

Продолжительность хранения (ч) (x)	1	3	6	8	10
Усушка (% к весу горячего хлеба) (y)	1,6	2,4	2,8	3,2	3,3

Требуется: а) найти оценки и остаточной дисперсии s²в предположении, что генеральное уравнение регрессии имеет вид; б) проверить при=0,05 значимость уравнения регрессии, т.е. гипотезу Н₀:=0; в) с надежностью=0,9 определить интервальные оценки параметров₀,₁; г) с надежностью=0,95 определить интервальную оценку условного математического ожиданияприх₀=6; д) определить при=0,95 доверительный интервал предсказанияв точкех=12.

2.7.На основании данных о динамике темпов прироста курса акций за 5 месяцев, приведенных в табл. 2.4.

Таблица 2.4.

месяцы (x)	0	1	2	3	4
y(%)	10	8	5	3	4

и предположения, что генеральное уравнение регрессии имеет вид , требуется: а) определить оценкиипараметров уравнения регрессии и остаточной дисперсии s²; б) проверить при=0,01 значимость коэффициента регрессии, т.е. гипотезы H₀:₁=0;

в) с надежностью =0,95 найти интервальные оценки параметров₀ и₁; г) с надежностью=0,9 установить интервальную оценку условного математического ожиданияприx₀=4; д) определить при=0,9 доверительный интервал предсказанияв точкеx=5.

2.8.Результаты исследования динамики привеса молодняка приведены в табл.2.5.

Таблица 2.5.

Возраст (недели) (x)	0	1	2	3	4	5	6
Вес (кг) (y)	1,2	2,5	3,9	5,2	6,4	7,7	9,2

Предполагая, что генеральное уравнение регрессии - линейное, требуется: а) определить оценки ипараметров уравнения регрессии и остаточной дисперсии s²; б) проверить при=0,05 значимость уравнения регрессии, т.е. гипотезы H₀:=0;

в) с надежностью =0,8 найти интервальные оценки параметров₀ и₁; г) с надежностью=0,98 определить и сравнить интервальные оценки условного математического ожиданияприx₀=3 иx₁=6;

д) определить при =0,98 доверительный интервал предсказанияв точкеx=8.

2.9.Себестоимость (y) одного экземпляра книги в зависимости от тиража (x) (тыс.экз.) характеризуется данными, собранными издательством (табл.2.6). Определить МНК-оценкиипараметров уравнения регрессии гиперболического вида, с надежностью=0,9 построить доверительные интервалы для параметров₀ и₁, а также условного математического ожиданияприx=10.

Таблица 2.6.

тираж (x) (тыс.экз.)	1	2	3	5	10	20	30	50
себестоимость (y)	9,10	5,30	4,11	2,83	2,11	1,62	1,41	1,30

2.10.Данные о расходе электроэнергии (кВт/ч) на изготовление одной тонны цемента (y) в зависимости от объема выпуска (x) продукции (тыс.т) цементными заводами приводятся в табл. 2.7.

Таблица 2.7.

Выпуск продукции x(тыс.т)	5	10	15	20	25	30
Расход электроэнергии у(кВт/ч)	10,0	8,2	7,3	6,3	6,4	5,2

Определить оценки ипараметров уравнения регрессии вида, проверить при=0,05 гипотезу Н₀:₁=0 и построить с надежностью=0,9 доверительные интервалы для параметров₀ и₁и условного математического ожиданияприx=20.

2.11.В табл. 2.8 представленные данные о темпах прироста (%) следующих макроэкономических показателейn=10 развитых стран мира за 1992г.: ВНП -x⁽¹⁾, промышленного производства -x⁽²⁾, индекса цен -x⁽³⁾.

Таблица 2.8.

Страны	x(1)	x(2)	x(3)
Япония	3,5	4,3	2,1
США	3,1	4,6	3,9
Германия	2,2	2,0	3,4
Франция	2,7	3,1	2,9
Италия	2,7	3,0	5,6
Великобритания	1,6	1,4	4,0
Канада	3,1	3,4	3,0
Австралия	1,8	2,6	4,0
Бельгия	2,3	2,6	3,4
Нидерланды	2,3	2,4	3,5

Примем за объясняемую величину (у) показательx⁽¹⁾, а за объясняющую (х) переменнуюx⁽²⁾и предположим, что уравнение регрессии имеет вид:

1. .

2. .

3. .

Требуется: а) определить (с учетом линеаризации уравнения) МНК-оценки ипараметров уравнения регрессии, оценкуостаточной дисперсии; б) проверить при=0,05 значимость коэффициента регрессии, т.е. Н₀:₁=0; в) с надежностью=0,9 найти интервальные оценки₀ и₁; г) найти при=0,95 доверительный интервал дляв точкех₀=х_i, гдеi=5; д) сравнить статистические характеристики уравнений регрессий: 1, 2 и 3.

2.12.Задачу 2.11 решить, приняв за объясняемую величину (у) показательx⁽¹⁾, а за объясняющую (х) переменнуюx⁽³⁾.