Матрица парных коэффициентов корреляций

	y	x(1)	x(2)	x(3)	x(4)	x(5)
y	1.00	0.43	0.37	0.40	0.58	0.33
x(1)	0.43	1.00	0.85	0.98	0.11	0.34
x(2)	0.37	0.85	1.00	0.88	0.03	0.46
x(3)	0.40	0.98	0.88	1.00	0.03	0.28
x(4)	0.58	0.11	0.03	0.03	1.00	0.57
x(5)	0.33	0.34	0.46	0.28	0.57	1.00

Анализ матрицы парных коэффициентов корреляции показывает, что результативный показатель наиболее тесно связан с показателем x⁽⁴⁾ — количество удобрений, расходуемых на 1 га ().

В то же время связь между признаками-аргументами достаточно тесная. Так, существует практически функциональная связь между числом колесных тракторов (x⁽¹⁾) и числом орудий поверхностной обработки почвы.

О наличии мультиколлинеарности свидетельствуют также коэффициенты корреляции и. Учитывая тесную взаимосвязь показателейx⁽¹⁾, x⁽²⁾и x⁽³⁾, в регрессионную модель урожайности может войти лишь один из них.

Чтобы продемонстрировать отрицательное влияние мультиколлинеарности, рассмотрим регрессионную модель урожайности, включив в нее все исходные показатели:

(2.8)

F_набл = 121.

В скобках указаны значения исправленных оценок среднеквадратических отклонений оценок коэффициентов уравнения .

Под уравнением регрессии представлены следующие его параметры адекватности: множественный коэффициент детерминации ; исправленная оценка остаточной дисперсии, средняя относительная ошибка аппроксимациии расчетное значение-критерия F_набл = 121.

Уравнение регрессии значимо, т.к. F_набл = 121 > F_kp = 2,85 найденного по таблицеF-распределения при=0,05;₁=6 и₂=14.

Из этого следует, что 0, т.е. и хотя бы один из коэффициентов уравнения_j(j = 0, 1, 2, ..., 5) не равен нулю.

Для проверки гипотезы о значимости отдельных коэффициентов регрессии H0: _j=0, гдеj=1,2,3,4,5, сравнивают критическое значениеt_kp= 2,14, найденное по таблицеt-распределения при уровне значимости=2Q=0,05 и числе степеней свободы=14, с расчетным значением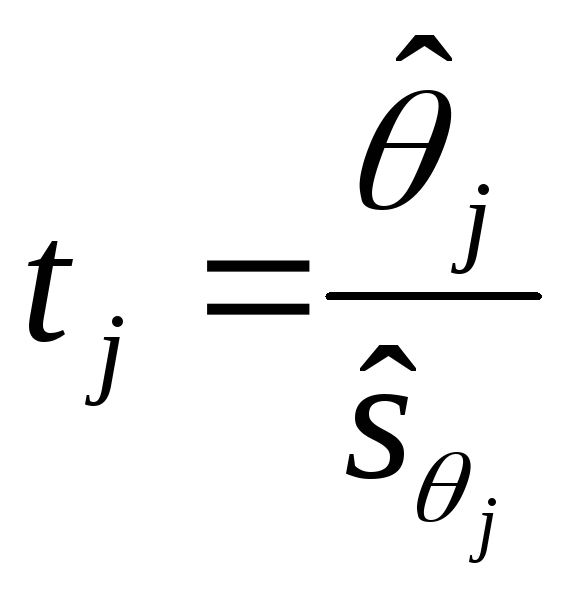. Из уравнения следует, что статистически значимым является коэффициент регрессии только при x⁽⁴⁾, так какt₄=2,90 >t_kp=2,14.

Не поддаются экономической интерпретации отрицательные знаки коэффициентов регрессии при x⁽¹⁾и x⁽⁵⁾. Из отрицательных значений коэффициентов следует, что повышение насыщенности сельского хозяйства колесными тракторами (x⁽¹⁾) и средствами оздоровления растений (x⁽⁵⁾) отрицательно сказывается на урожайности. Таким образом, полученное уравнение регрессии неприемлемо.

Для получения уравнения регрессии со значимыми коэффициентами используем пошаговый алгоритм регрессионного анализа. Первоначально используем пошаговый алгоритм с исключением переменных.

Исключим из модели переменную x⁽¹⁾, которой соответствует минимальное по абсолютной величине значениеt₁=0,01. Для оставшихся переменных вновь построим уравнение регрессии:

Полученное уравнение значимо, т.к. F_набл = 155 > F_kp = 2,90, найденного при уровне значимости=0,05 и числах степеней свободы₁=5 и₂=15 по таблицеF-распределения, т.е. вектор0. Однако в уравнении значим только коэффициент регрессии приx⁽⁴⁾. Расчетные значенияt_jдля остальных коэффициентов меньшеt_кр= 2,131, найденного по таблицеt-распределения при=2Q=0,05 и=15.

Исключив из модели переменную x⁽³⁾, которой соответствует минимальное значениеt₃=0,35 и получим уравнение регрессии:

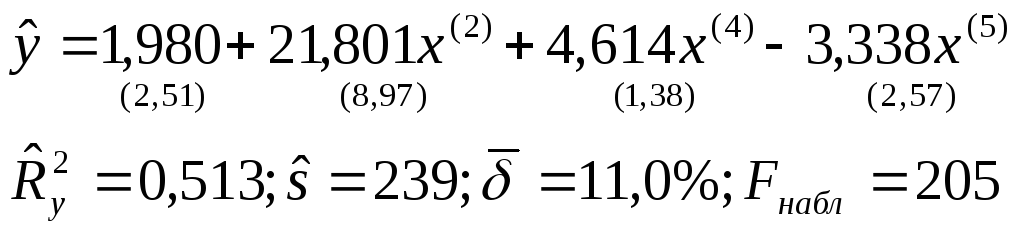(2.9)

В полученном уравнении статистически не значим и экономически не интерпретируем коэффициент при x⁽⁵⁾. Исключивx⁽⁵⁾получим уравнение регрессии:

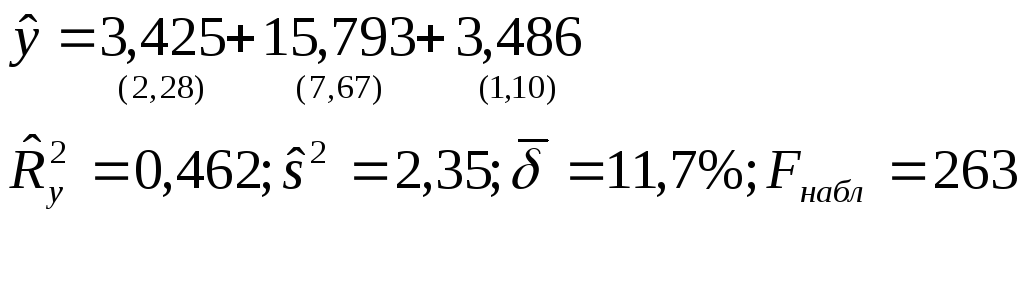(2.10)

Мы получили значимое уравнение регрессии со значимыми и интерпретируемыми коэффициентами.

Однако полученное уравнение является не единственно “хорошей” и не “самой лучшей” моделью урожайности в нашем примере.

Покажем, что в условии мультиколлинеарности пошаговый алгоритм с включением переменных является более эффективным.На первом шаге в модель урожайностиyвходит переменная x⁽⁴⁾, имеющая самый высокий коэффициент корреляции сy, объясняемой переменнойr(y, x⁽⁴⁾)=0,58. На втором шаге, включая уравнение наряду сx⁽⁴⁾переменныеx⁽¹⁾илиx⁽³⁾, мы получим модели, которые по экономическим соображениям и статистическим характеристикам превосходят (2.10):

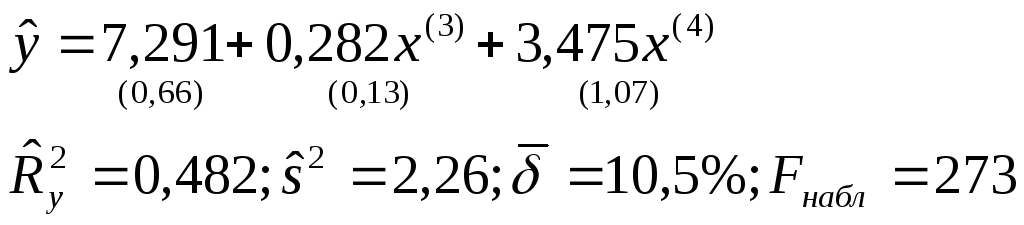(2.11)

и

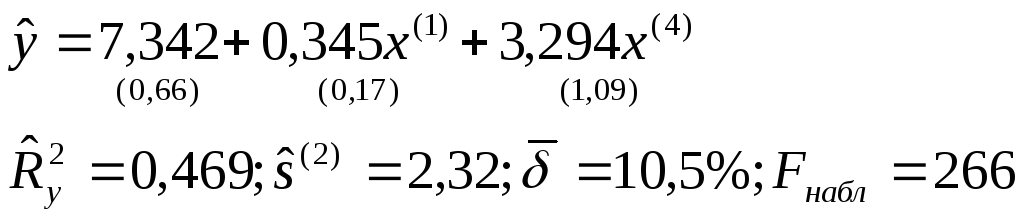(2.12)

Включение в уравнение любой из трех оставшихся переменных ухудшает его свойства. Смотри, например, уравнение (2.9).

Таким образом, мы имеем три “хороших” модели урожайности, из которых нужно выбрать по экономическим и статистическим соображениям одну.

По статистическим критериям наиболее адекватна модель (2.11). Ей соответствуют минимальные значения остаточной дисперсии =2,26 и средней относительной ошибки аппроксимациии наибольшие значенияи F_набл = 273.

Несколько худшие показатели адекватности имеет модель (2.12), а затем — модель (2.10).

Будем теперь выбирать наилучшую из моделей (2.11) и (2.12). Эти модели отличаются друг от друга переменными x⁽¹⁾иx⁽³⁾. Однако в моделях урожайностей переменнаяx⁽¹⁾(число колесных тракторов на 100 га) более предпочтительна, чем переменнаяx⁽³⁾(число орудий поверхностной обработки почвы на 100 га), которая является в некоторой степени вторичной (или производной от x⁽¹⁾).

В этой связи из экономических соображений предпочтение следует отдать модели (2.12). Таким образом, после реализации алгоритма пошагового регрессионного анализа с включением переменных и учета того, что в уравнение должна войти только одна из трех связанных переменных (x⁽¹⁾,x⁽²⁾илиx⁽³⁾) выбираем окончательное уравнение регрессии:

Уравнение значимо при =0,05, т.к. F_набл = 266 > F_kp = 3,20, найденного по таблицеF-распределения при=Q=0,05;₁=3 и₂=17. Значимы и все коэффициенты регрессииив уравненииt_j>t_kp(=2Q=0,05;=17)=2,11. Коэффициент регрессии₁следует признать значимым (₁0) из экономических соображений, при этомt₁=2,09 лишь незначительно меньшеt_kp= 2,11.

Из уравнения регрессии следует, что увеличение на единицу числа тракторов на 100 га пашни (при фиксированном значении x⁽⁴⁾) приводит к росту урожайности зерновых в среднем на 0,345 ц/га.

Приближенный расчет коэффициентов эластичности э₁0,068 и э₂0,161 показывает, что при увеличении показателейx⁽¹⁾иx⁽⁴⁾на 1% урожайность зерновых повышается в среднем соответственно на 0,068% и 0,161%.

Множественный коэффициент детерминации свидетельствует о том, что только 46,9% вариации урожайности объясняется вошедшими в модель показателями (x⁽¹⁾иx⁽⁴⁾), то есть насыщенностью растениеводства тракторами и удобрениями. Остальная часть вариации обусловлена действием неучтенных факторов (x⁽²⁾,x⁽³⁾,x⁽⁵⁾, погодные условия и др.). Средняя относительная ошибка аппроксимациихарактеризует адекватность модели, так же как и величина остаточной дисперсии. При интерпретации уравнения регрессии интерес представляют значения относительных ошибок аппроксимации. Напомним, что— модельное значение результативного показателя, характеризует среднее для совокупности рассматриваемых районов значение урожайности при условии, что значения объясняющих переменныхx⁽¹⁾иx⁽⁴⁾зафиксированы на одном и том же уровне, а именноx⁽¹⁾=x_i⁽¹⁾иx⁽⁴⁾ = x_i⁽⁴⁾. Тогда по значениям_iможно сопоставлять районы по урожайности. Районы, которым соответствуют значения_i>0, имеют урожайность выше среднего, а_i<0 — ниже среднего.

В нашем примере, по урожайности наиболее эффективно растениеводство ведется в районе, которому соответствует ₇=28%, где урожайность на 28% выше средней по региону, и наименее эффективно — в районе с₂₀=27,3%.