1.3. Тест

1. Известно, что при фиксированном значении x₃между величинамиx₁иx₂существует положительная связь. Какое значение может принять частный коэффициент корреляцииr_12/3.

а) -0,8; в) 0,4;

б) 0; г) 1,3.

2. По результатам n=20 наблюдений получен частный коэффициент корреляции. Определите, чему при уровне значимости=0,05 равна разность между наблюдаемыми критическим (r_kp) значениями коэффициентов корреляции:

а) -0,513; в) 0,700;

б) 0,344; г) 0,133.

3. Известно, что x₃усиливает связь между величинамиx₁иx₂. По результатам наблюдений получен частный коэффициент корреляции. Какое значение может принять парный коэффициент корреляции:

а) 0,4; в) -0,8;

б) 0,2; г) 1,2.

4. По результатам n=10 наблюдений рассчитан частный коэффициент корреляциии с доверительной вероятностью=0,95 найдена интервальная оценка 0,37r₁₂₍₃₎0,96. Какое значение принимает верхняя граница доверительного интервала дляr₁₂₍₃₎ при=0,9:

а) 0,94; в) 0,39;

б) 0,98; г) 0,27.

5. По результатам n=20 наблюдений рассчитани найден при=0,95 доверительный интервал 0,23r₁₃₍₂₎0,83.

Какое значение примет нижняя граница доверительного интервала для r₁₃₍₂₎ приn=10 еслииостались неизменными:

а) 0,45;

б) 0,20;

в) 0,32;

г) 0,89.

6. Множественный коэффициент корреляции . Определите, какой процент дисперсии величиныx₁объясняется влияниемx₂иx₃:

а) 28%;

б) 32%;

в) 64%;

г) 80%.

7. По результатам 20 наблюдений найден множественный коэффициент корреляции, т.е. гипотизу . Проверьте значимость множественного коэффициента корреляции H₀:при=0,05 и определите разность между наблюдаемым F_набли критическим F_kpзначениями статистики критерия:

а) 2,8;

б) -13,6;

в) 9,4;

г) 11,5.

8. Какое значение может принимать коэффициент детерминации:

а) -0,5;

б) -0,2;

в) 0,4;

г) 1,2.

9. Какое значение может принять множественный коэффициент корреляции:

а) -1;

б) -0,5;

в) 0;

г) 1,2.

10. По результатам n=25 наблюдений получен парный коэффициент корреляции. Известно, чтоx₃занижает связь междуx₁иx₂. Какое значение может принять частный коэффициент корреляции:

а) -0,5;

б) -0,6;

в) 0,5;

г) 0,8.

Глава 2. Регрессионный анализ (классическая модель)

2.1. Регрессионная модель производительности труда

По данным годовых отчетов десяти (n=10) машиностроительных предприятий провести регрессионный анализ зависимости производительности трудау(тыс. руб. на чел.) от объема производствах(млн.руб.). Предполагается линейная модель, т.е..

Таблица 2.1.

Исходная информация для анализа и результаты расчетов

номер п/п (i)	yi	xi
1	2,1	3	2,77	-0,67
2	2,8	4	3,52	-0,72
3	3,2	5	4,27	-1,07
4	4,5	5	4,27	0,23
5	4,8	5	4,27	0,53
6	4,9	5	4,27	0,63
7	5,5	6	5,02	0,48
8	6,5	7	5,77	0,73
9	12,1	15	11,75	0,35
10	15,1	20	15,50	-0,4

Решение:Определим вектор оценоккоэффициентов регрессии. Согласно методу наименьших квадратов, векторbполучается из выражения:

(2.1)

Воспользовавшись правилами умножения матриц будем иметь

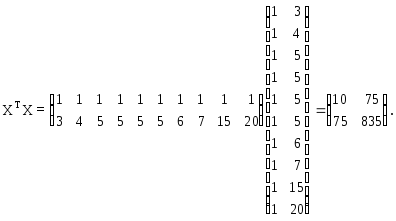
В матрице число 10, лежащее на пересечении 1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки матрицы Х^Ти 1-го столбца матрицы Х, а число 75, лежащее на пересечении 1-й строки и 2-го столбца - как сумма произведений элементов 1-й строки матрицы Х^Ти 2-го столбца матрицы Х и т.д.

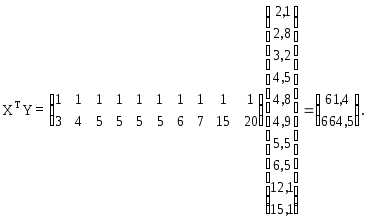
Найдем обратную матрицу

Тогда вектор оценок коэффициентов регрессии равен

а оценка уравнения регрессии будет иметь вид

(2.2)

Перейдем к статистическому анализу полученного уравнения регрессии: проверке значимости уравнения и его коэффициентов, исследованию абсолютных и относительныхошибок аппроксимации.

Предварительно определим вектор модельных значений результативного показателя :

Тогда

(2.3)

А несмещенная оценка остаточной дисперсии равна:

а оценка среднеквадратического отклонения

.

Проверим на уровне значимости =0,05 значимость уравнения регрессии, т.е гипотезу H₀:=0 (₀=₁=0). Для этого вычисляем величину

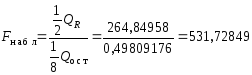(2.4)

По таблице F-распределения для =0,05,₁=2 и₂=8 находим F_кр=4,46. Так как F_набл>F_кр, то уравнение является значимым.

Найдем оценку ковариационной матрицы вектора :

(2.5)

Отсюда получаем несмещенные оценки дисперсий и среднеквадратических отклонений коэффициентов регрессии:

Для проверки значимости коэффициента регрессии, т.е. гипотезы Н₀:₁=0, находим по таблице t-распределения при=0,05,=8 значение t_кр=2,31:

(2.6)

Так как больше t_кр=2,31, то коэффициент регрессии₁значимо отличается от нуля. Таким образом, окончательное уравнение регрессии имеет вид

Определим интервальные оценки коэффициентов уравнения с доверительной вероятностью =0,95. Т.к.

(2.7)

где j=0; 1, то

₀[0,5252,310,391], откуда0,378₀1,428 и

₁[0,748612,310,0428], откуда 0,650₁0,847.

Приведенные неравенства подтверждают вывод о значимости ₁(₁0). В то же время коэффициент₀уравнения (2.2) не значим (границы доверительного интервала имеют разные знаки).