2.2. Вычисление определителей

Определение: Определителем n-го порядка, соответствующим квадратной матрице

,

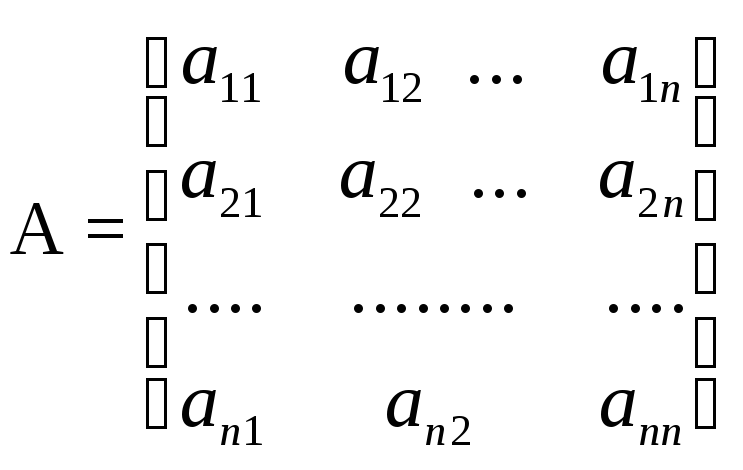называется алгебраическая сумма n!¹ членов, каждый из которых есть произведение n элементов матрицы, взятых по одному из каждой строки и из каждого столбца, причем член берется со знаком плюс, если его индексы составляют четную перестановку, и со знаком минус — в противном случае:

,

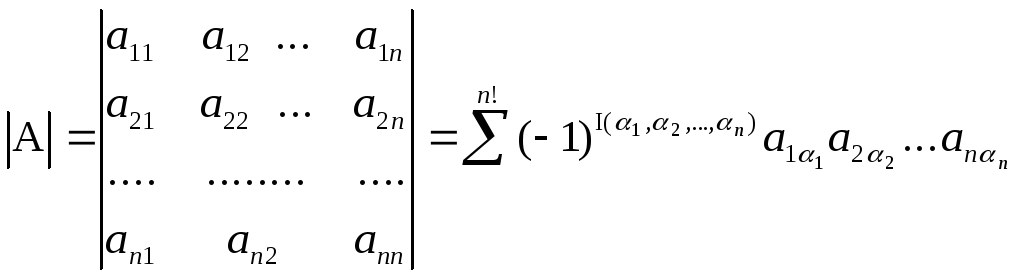где суммирование распространяется на всевозможные перестановки изn чисел 1, 2,...., n.

Несмотря на громоздкость определения, в первую очередь, следует запомнить, что определитель – это число, характеризующее квадратную матрицу.

Вычисление определителей n-го порядка производится на основании свойств определителей и теоремы Лапласа.

Перечислим основные свойства определителей, опуская доказательства:

1. Если какая-либо строка (столбец) матрицы состоит из одних нулей, то её определитель равен нулю.

2. Если все элементы какой-либо строки (столбца) матрицы умножить на число , то её определитель умножится на это число.

3. При транспонировании матрицы её определитель не изменяется:

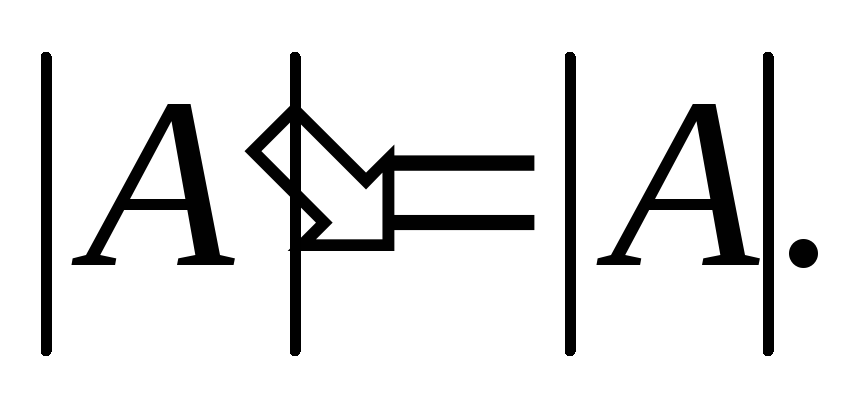
4. При перестановке двух строк (столбцов) матрицы её определитель меняет знак на противоположный.

5. Если квадратная матрица содержит две одинаковые строки (столбца), то её определитель равен нулю.

6. Если элементы двух строк (столбцов) матрицы пропорциональны, то её определитель равен нулю.

7. Определитель матрицы не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число.

Минором элементаматрицыn-го порядка называется определитель матрицы (n-1)-го порядка, полученной из матрицы A вычёркиванием i-й строки и j-го столбца.

Алгебраическим дополнением элементаматрицыn-го порядка называется его минор, взятый со знаком

т.е. алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца (I + j) – чётное число, и отличается от минора знаком, когда (I + j) – нечётное число.

Теорема 2.1 (Лапласа). Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:

(разложение по элементам i-й строки; I = 1, 2,…, n).

Пример 2.5. Вычислить определитель второго порядка матрицы A:

.

Решение. Определитель второго порядка непосредственно вычисляется по формуле

Пример 2.6. Вычислить определитель третьего порядка матрицы B:

.

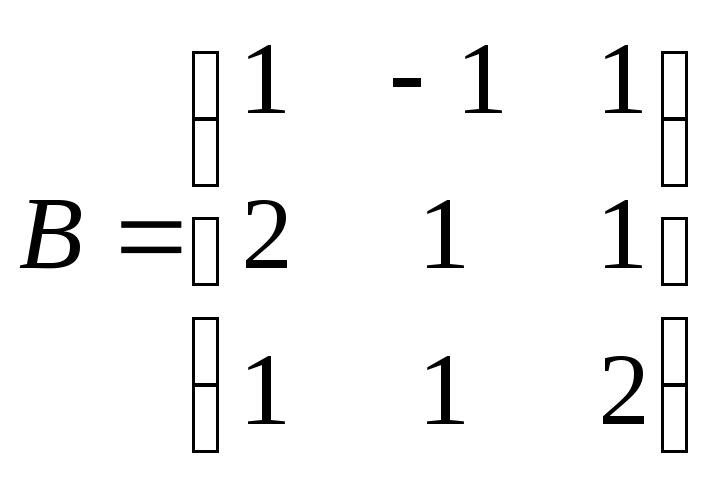Решение. Определитель третьего порядка вычисляется по формуле

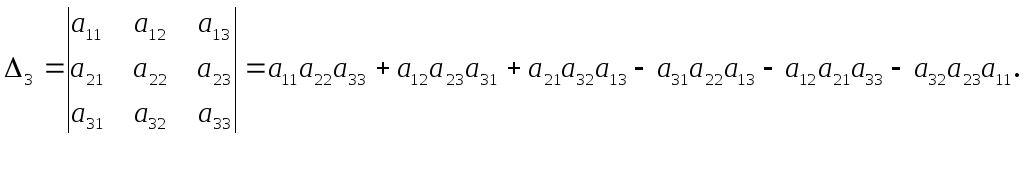
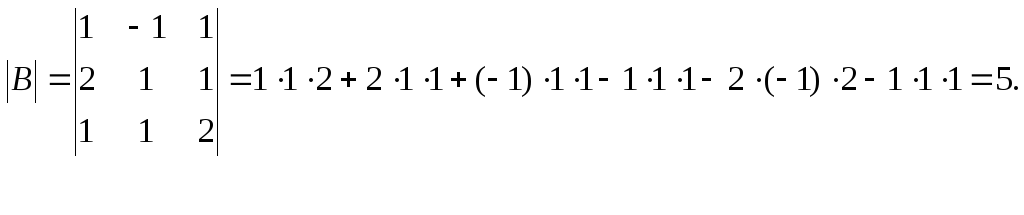
Пример 2.7. Вычислить определитель:

.

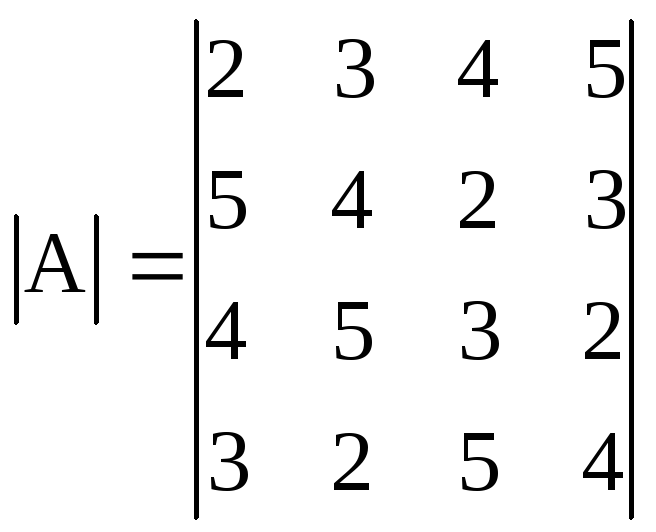Решение. В каком-либо столбце (строке) определителя получим единицу. Для этого осуществим следующее преобразование: из элементов второго столбца вычтем соответствующие элементы первого столбца. На основании свойств определителя величина определителя при этом не изменится:

.

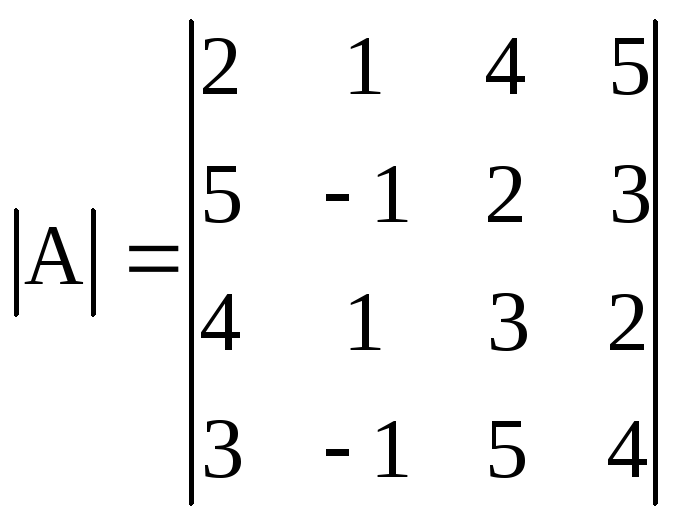Второй столбец преобразуем так, чтобы все элементы его, за исключением элемента а₁₂ = 1, были равны нулю. Для этого прибавим первую строку ко второй и четвертой, а из третьей строки вычтем первую. Получим

.

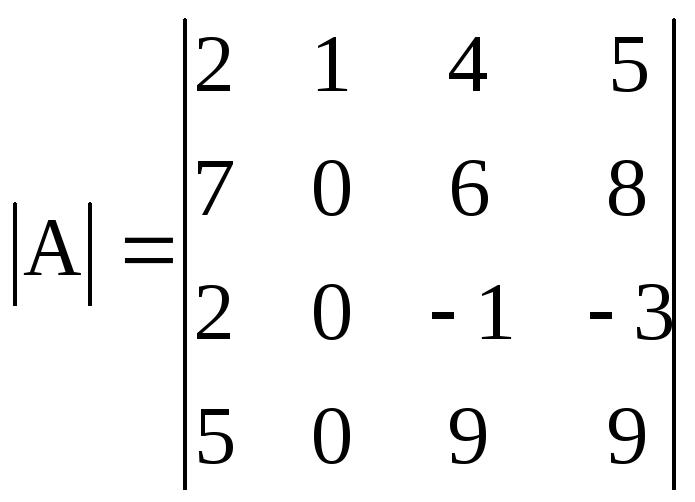Разложим определитель по элементам второго столбца:

.

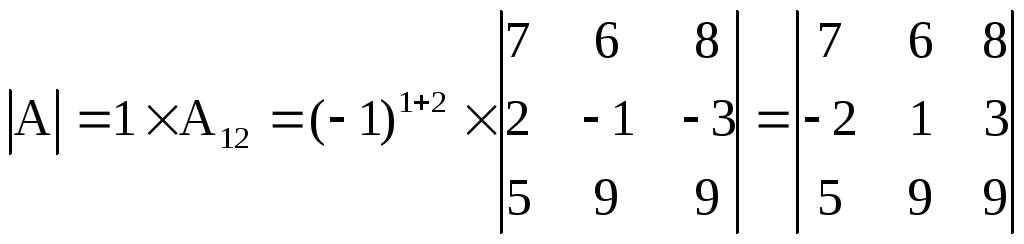В результате получим определитель третьего порядка. Преобразуем данный определитель, получая единицу с нулями во второй строке:

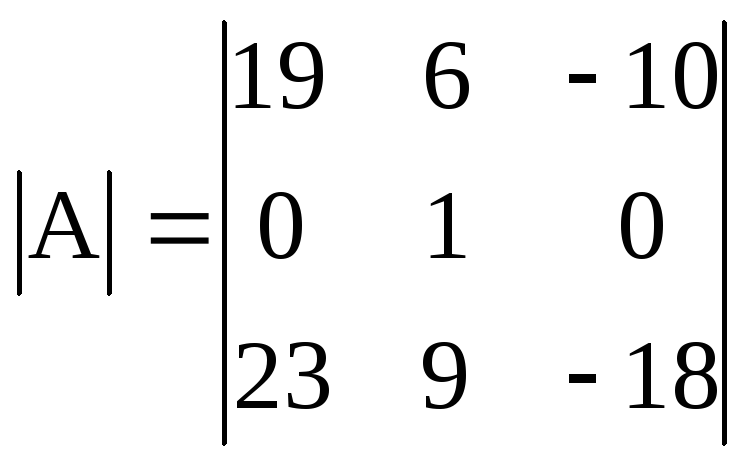
Разложим определитель по элементам второй строки:

.

Квадратная матрица А порядка n называется невырожденной (неособенной), если ее определитель отличен от нуля. В противном случае матрица А называется особенной (вырожденной).

Теорема 2.2. Для всякой невырожденной матрицы А=(а_ij)_m,n существует единственная обратная матрица, равная

,

где А* – присоединенная матрица, каждый элемент которой есть алгебраическое дополнение¹ элемента а_ij матрицы А, т.е.

.

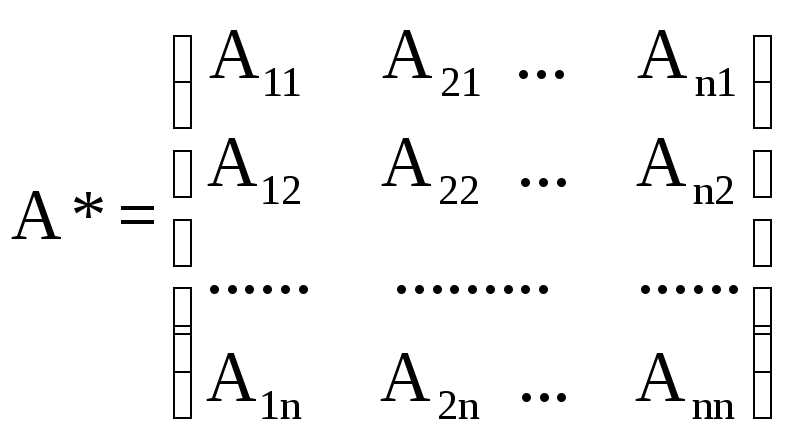Пример 2.8. Вычислить обратную матрицу для матрицы А:

.

Решение. Вычислим определитель матрицы: .

Определитель матрицы А отличен от нуля, следовательно, для матрицы А существует единственная обратная матрица. Вычислим присоединенную матрицу А*:

.

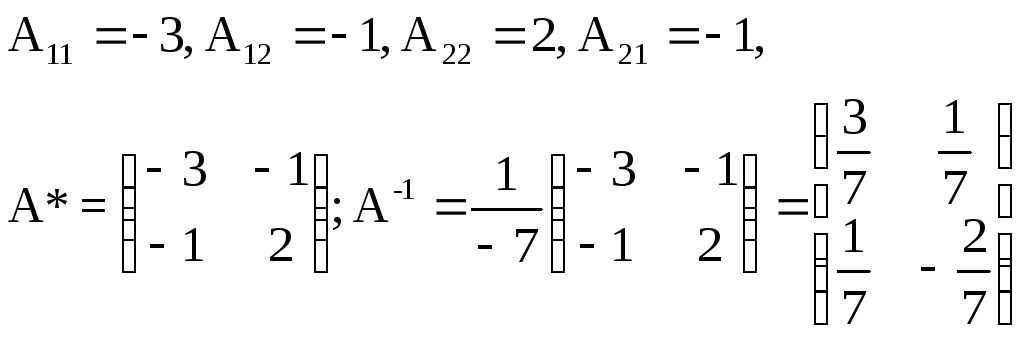Сделав проверку, убеждаемся, что АА^-1 = Е.