Тема 4.

Теория двойственности в линейном программировании

Для изучения данного раздела дисциплины необходимы знания, полученные при изучении темы 3.

Изучив данную тему, студент должен:

• знать основные положения теории двойственности;

• уметь записывать двойственную задачу для любых постановок исходной задачи;

• иметь общие представления об анализе решения ЗЛП с помощью теории двойственности и анализе решения ЗЛП на основе отчетов MS EXCEL;

• использовать отчеты, полученные с помощью MS Excel, для анализа на чувствительность.

Цель изучения – получить представление о теории двойственности и осознать ее экономическую значимость.

В данном разделе вводится важное понятие теории линейного программирования – понятие двойственности. Двойственная задача – это вспомогательная задача линейного программирования (ЛП), формулируемая с помощью определённых правил непосредственно из условий исходной (прямой) задачи. Часто рассматриваются формулировки двойственной задачи, соответствующие различным формам записи прямой задачи. Однако опыт показывает, что на начальной стадии изучения ЛП детали различных формулировок двойственной задачи нередко затрудняют восприятие материала. Кроме того, практическое использование теории двойственности не требует знания деталей различных формулировок двойственной задачи. Здесь даётся обобщённая формулировка двойственной задачи ЛП, которая применима к любой форме представления прямой задачи. Это объясняется тем, что использование симплексного и других методов решения задач ЛП требует приведения ограничений любой задачи ЛП к стандартной (канонической) форме, поэтому двойственная задача будет сформулирована в соответствии со стандартной формой ограничений прямой задачи.

4.1. Определение и экономический смысл двойственной злп

Пусть прямая задача записана с ограничениями в каноническом виде:

; (4.1)

; (4.2)

. (4.3)

Задачей, двойственной к ЗЛП (4.1)–(4.3), называется следующая ЗЛП:

; (4.4)

; (4.5)

не ограничены в знаке, i = 1… m. (4.6)

Двойственная ЗЛП строится по следующим правилам:

1) Каждому ограничению прямой задачи соответствует переменная двойственной задачи, т.е. число переменных двойственной задачи равно числу ограничений прямой задачи.

2) Каждой переменной прямой задачи соответствует ограничение двойственной задачи, т.е. число ограничений двойственной задачи равно числу переменных прямой задачи.

3) Матрица функциональных ограничений двойственной задачи получается путем транспонирования матрицы функциональных ограничений прямой задачи.

4) Вектор целевой функции прямой задачи становится вектором правой части ограничений двойственной задачи, а векторправой части прямой задачи – вектором целевой функции двойственной задачи.

5) Если ЦФ прямой задачи максимизируется, то ЦФ двойственной задачи минимизируется, а ограничения имеют вид ≥, и наоборот.

Прямая задача	Двойственная задача
P =	Q = –не ограничен в знаке	(4.7)
P =	Q = не ограничен в знаке	(4.8)

Пример 4.1. Пусть прямая задача записана в виде основной ЗЛП:

(4.9)

Приведем ограничения задачи (4.9) к канонической форме:

(4.10)

Тогда двойственная задача (ДЗ) будет иметь вид:

.

(4.11)

Пример 4.2.

Прямая задача:

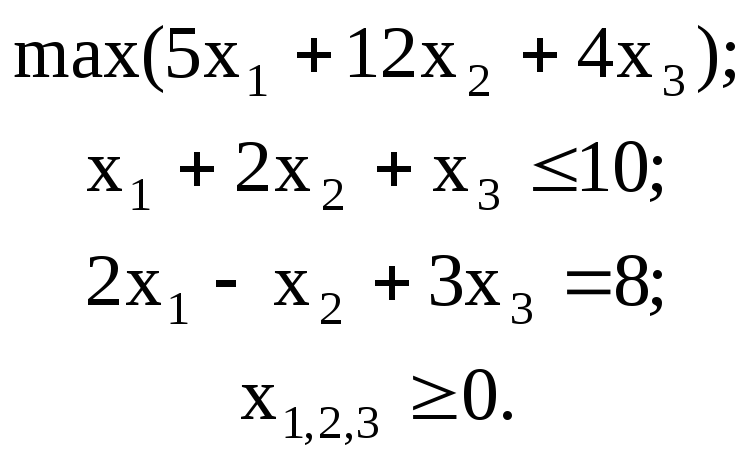
Прямая задача с ограничениями в канонической форме:

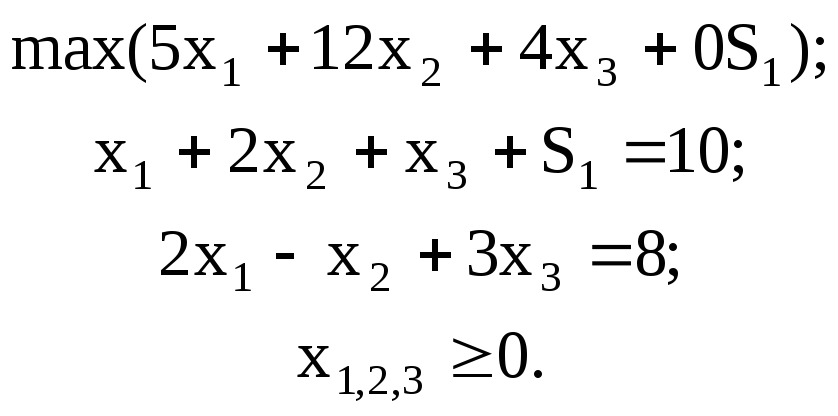
S₁ ≥ 0

Двойственная задача:

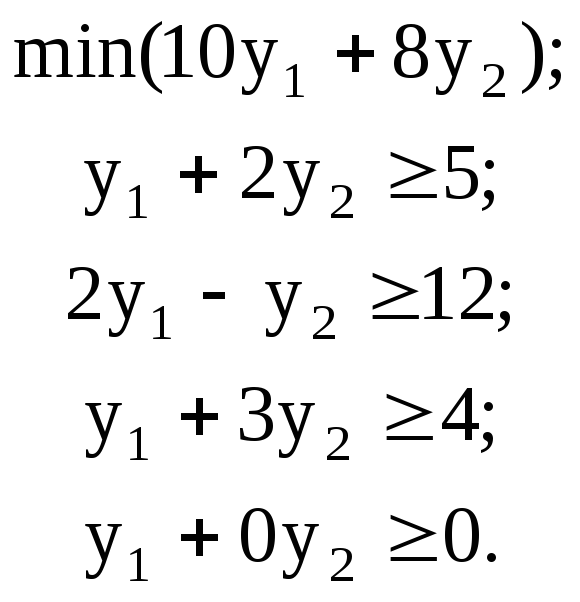
y_1,2 не ограничены в знаке.

Ограничение , т.е., является более жестким, чем условие неограниченностиу₁ в знаке, поэтому двойственная задача может быть записана в следующем виде:

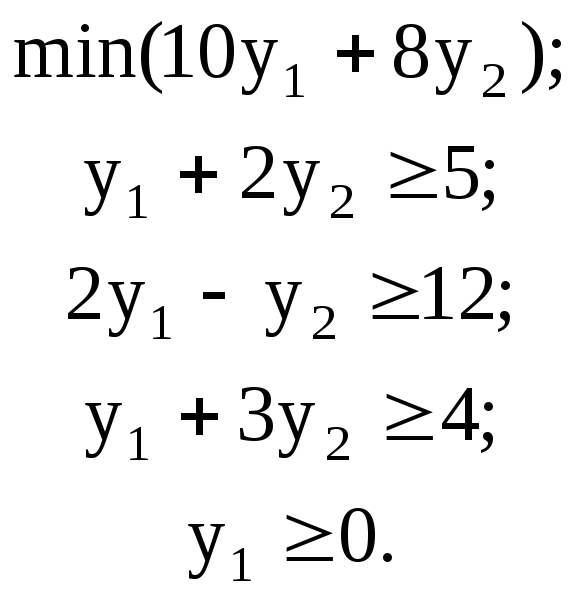
у₂ не ограничена в знаке.

Пример 4.3. Прямая задача:

min(5X₁ – 2X₂);

–X₁ + X₂ ≥ –3;

2X₁ + 3X₂ ≤ 5;

X_1,2 ≥ 0.

Прямая задача с ограничениями в канонической форме:

min(5X₁ – 2X₂ + 0S₁ + 0S₂);

–X₁ + X₂ – S₁ = –3;

2X₁ + 3X₂ + S₂ = 5;

Двойственная задача:

max(–3У₁ + 5У₂);

–У₁ + 2У₂ ≤ 5;

У₁ + 3У₂ ≤ –2;

–У₁ + 0У₂ ≤ 0;

0У₁ + У₂ ≤ 0.

У_1,2 не ограничены в знаке.

Отбрасывая избыточные ограничения, получаем:

max(–3У₁ + 5У₂);

–У₁ + 2У₂ ≤ 5;

У₁ + 3У₂ ≤ –2;

У₁ ≥ 0, У₂ ≤ 0.

Пример 4.4. Прямая задача:

max(5X₁ + 6X₂);

X₁ + 2X₂ = 5;

–X₁ + 5X₂ ≥ 3;

4X₁ + 7X₂ ≤ 8.

X₁ не ограничена в знаке, X₂ ≥ 0.

Прямая задача с ограничениями в канонической форме:

max(5– 5 + 6X₂ + 0S₁ + 0S₂);

+ 2X₂ = 5;

+ 5X₂ – S₁ = 3;

4 + 7X₂ + S₂ = 8;

Двойственная задача:

min(5У₁ + 3У₂ + 8У₃);

У₁ – У₂ + 4У₃ ≥ 5;

–У₁ + У₂ – 4У₃ ≥ –5;

2У₁ + 5У₂ + 7У₃ ≥ 6;

0У₁ – У₂ + 0У₃ ≥ 0;

0У₁ + 0У₂ + У₃ ≥ 0.

У_1,2,3 не ограничены в знаке.

Заметим, что первое и второе ограничения двойственной задачи можно заменить одним ограничением в виде равенства, избыточные ограничения на У₂ и У₃ можно отбросить. В итоге получаем:

min(5У₁ + 3У₂ + 8У₃);

У₁ – У₂ + 4У₃ = 5;

2У₁ + 5У₂ + 7У₃ ≥ 6;

У₁ не ограничена в знаке;

У₂ ≤ 0, У₃ ≥ 0.

Очевидно, что задача, двойственная к двойственной, совпадает с прямой.