5. Закон Релея

Распределение таких существенно положительных величин, как эксцентриситет, биение, разностенность, непараллельность, неперпендикулярность, овальность, конусообразность, и некоторых других, характеризующихся их абсолютными значениями (т.е. без учета знака), подчиняется закону распределения эксцентриситета (закону Релея).

Распределение по закону Релея формируется, в частности, тогда, когда случайная величина Rявляется радиус-вектором при двумерном гауссовом распределении, т.е. если она представляет собой геометрическую сумму двух случайных величинXиY,

,

каждая из которых подчиняется закону Гаусса с параметрами

L_Xср =L_Yср =L_Rср=0 и

σ_X= σ_Y= σ₀

Закон распределения Релея однопараметрический, и уравнение его кривой распределения имеет вид (см. рис.4)

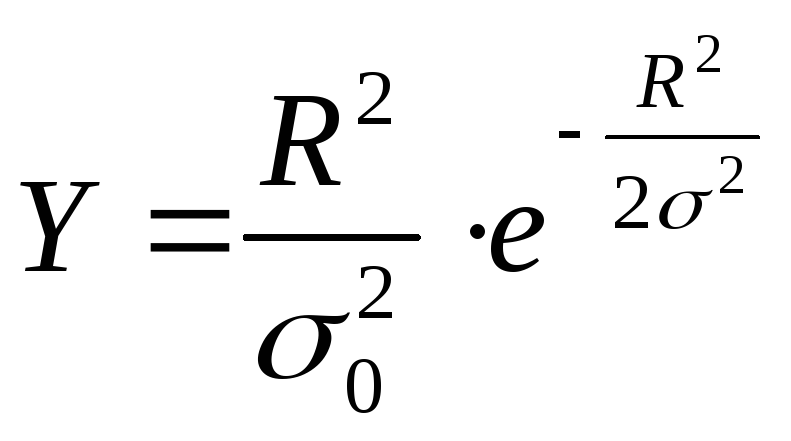, (1)

где σ₀ – среднее квадратическое отклонение значений координатXиY.

Рис.4 Распределение размеров по закону Релея.

Уравнение (1) показывает, что при R=0Y=0, т.е. начало кривой распределения совпадает с началом координат. Нисходящая ветвь этой кривой асимптотически приближается к оси абсцисс, так как приY=0R→∞.

Для теоретической кривой распределения по закону Релея (рис.4) характерны крутой подъем восходящей ветви и более пологий спуск нисходящей ветви. Вершина кривой более заострена, чем у кривой нормального распределения, и смещена от среднего значения переменной величины Rв сторону начала координат.

5.1. Основные параметры закона Релея

Среднее арифметическое R_српеременной случайной величины (эксцентриситета, биения, разностенность и др.), ее среднее квадратическое отклонение σ_R и среднее квадратическое отклонение σ₀значений координатXиYконца радиус-вектораRсвязаны между собой следующими соотношениями:

(2)

R_ср=1,92∙σ_R=1,253∙σ₀ (3)

Фактическое поле рассеивания значений переменной величины радиус-вектора R(эксцентриситета, биения, разностенность и др.) находят из выражений:

∆=5,252∙σ_R; (4)

∆=3,44∙σ₀; (5)

При анализе погрешностей обработки конкретных заготовок расчетное значение среднего квадратического отклонения σ_Rрадиус вектора определяют по величине среднего квадратичногоS, установленного путем измерений партии – выборки деталей и последующего вычисления по формуле (6)

=, (6)

где S– среднее квадратическое отклонение;

X_i – текущий действительный размер;

(7)

– среднее арифметическое значение действительных размеров заготовок данной партии;

m_i – частота (количество заготовок данного интервала размеров)

n– количество заготовок в партии;

Для перехода от эмпирической величины Sк расчетной σ_Rиспользуют уравнение

σ_R=p∙S , (8)

где p–поправочный коэффициент, учитывающий погрешность определения среднего квадратического отклонения при малых размерах партии измеренных заготовокNсм. таблицу №2. [1]

Таблица №2

N, шт.	∆S, %	p
25	42.4	1.4
50	30.0	1.3
75	25.0	1.25
100	21.2	1.2
200	15.0	1.15
300	12.2	1.12
400	10.6	1.11
500	10.0	1.10