Свойства преобразования Лапласа

1. Линейность ℒ;.

2. Теорема смещения: ℒ.

3. Дифференцирование ℒ,

ℒ.

4. Интегрирование ℒ; ;

5. Теорема умножений (свертка) ℒ,

где ;.

6. Теорема подобия ℒ.

7. Теорема о начальном значении .

8. Теорема о предельном значении .

Примеры преобразования Лапласа для некоторых функций:

Оригинал Изображение

;

;

;

;

;

;

;

(ступенчатая функция);

(импульсный сигнал).

Передаточная функция звена

Передаточной функцией звена называется отношение изображения выходного сигнала к изображению входного сигнала звена.

Иногда для описания передаточных функций звена используется обозначение K(s).

Связь оператора s с физикой

В линейной системе переходный процесс, описываемый дифференциальным уравнением, может быть очень сложной функцией времени, но весь он состоит из линейной комбинации двух видов кривых – экспонент и синусоид.

При этом в устойчивой системе все экспоненты затухающие. Оператор Лапласа s- число комплексное:.

с– свидетельствует о величине экспоненты;

- характеризует частоту.

Частотные характеристики звеньев

Переход от передаточной функции звена осуществляется простой заменой .

То есть из рассматриваемого процесса как бы исключается экспонента. Физически частотные характеристики звена имеют очень простую интерпретацию.

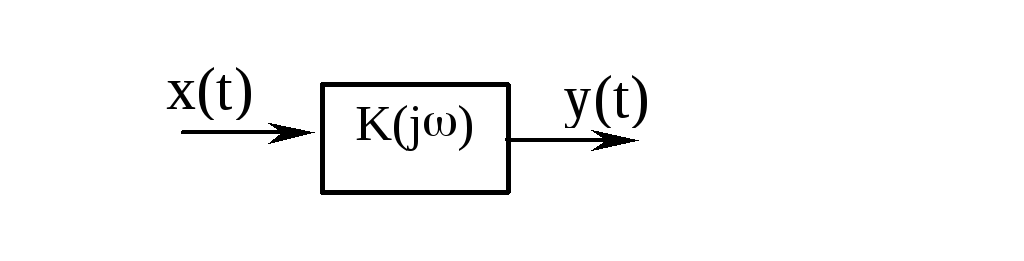
Пусть - синосоидальное входное воздействие.

Тогда в установившемся режиме выходной сигнал также будет синусоидальным: .

Комплексный коэффициент усиления .

может быть получен экспериментально, либо путем подстановки в передаточную функцию звена вместо . .

- АЧХ – амплитудно-частотная характеристика звена;

- ФЧХ – фазо-частотная характеристика звена.

Таким образом - АФЧХ - амплитудно-фазовая частотная характеристика.

- ВЧХ – вещественная частотная характеристика;

- МЧХ – мнимая частотная характеристика.

Можно по ВЧХ и МЧХ определить АЧХ и ФЧХ:

;

Логарифмические частотные характеристики лах и лфх

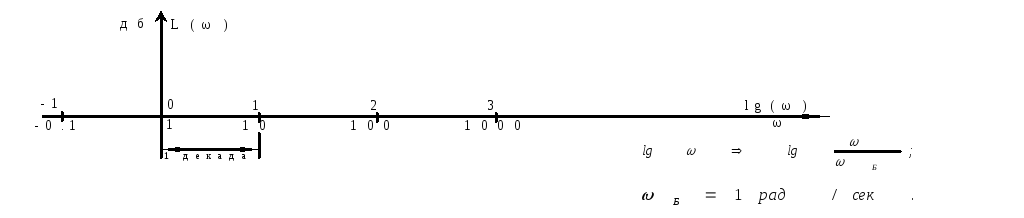
По оси ординат откладываются в логарифмическом масштабе значения . .

Из разделов физики известно, что (мощность) и .

- [Белл],

- [децибелл].

По оси абсцисс откладывается угловая частота (относительное значение). Если откладывается в логарифмическом масштабе по основанию 10 (как на рисунке), то единицей измерения являетсядекада. Если (в логарифмическом масштабе по основанию 2),то вместо декады будетоктава.

Логарифмические характеристики применяются из-за их удобства, так как при последовательном соединении звеньев характеристики этих звеньев, построенные в логарифмическом масштабе, складываются. Поэтому методы анализа и синтеза с помощью ЛАХ очень просты.

Если АЧХ чаще всего очень сложные функции от , то ЛАХ легко аппроксимируются отрезками прямых.

Регулярные сигналы

Сигналы на входе звена – произвольная временные функции. Чтобы иметь возможность изучать поведение звеньев при прочих равных условиях вводится 3 вида регулярных сигналов:

1. Единичное ступенчатое воздействие

2. Импульсный сигнал

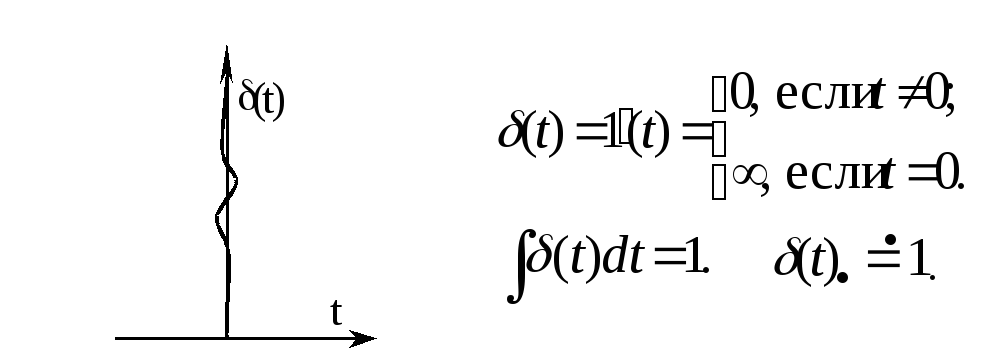
Реально - импульс достаточно короткий с крутыми фронтами.

3. Гармоничный сигнал .

Каждый из трех названных сигналов позволяет изобразить сигнал произвольной формы.

Эти регулярные сигналы сами по себе являются удачными для исследования статических и динамических свойств звеньев и систем, так как в спектре и содержатся частоты от самых малых до очень больших значений, а гармонический сигнал сам может принимать любые значения частот.