
- •Устойчивость систем автоматического управления Понятие устойчивости системы
- •Критерии устойчивости
- •Алгебраический критерий устойчивости Раусса. 1875г.
- •Критерий устойчивости Гурвица. 1895 г.
- •О критическом коэффициенте усиления
- •Частотные критерии устойчивости
- •Принцип аргумента
- •Критерий устойчивости Михайлова
- •Частотный критерий устойчивости Найквиста
- •Обобщенная формулировка критерия Найквиста
- •Логарифмический критерий устойчивости (Найквиста)
- •О применении критериев устойчивости
Обобщенная формулировка критерия Найквиста
Для устойчивости
замкнутой системы необходимо и достаточно,
чтобы годограф АФЧХ разомкнутой системы
при изменении
от 0 до![]() сделал число положительных переходов
действительной оси левее точки (
сделал число положительных переходов
действительной оси левее точки (![]() )
больше числа отрицательных переходов
на
)
больше числа отрицательных переходов
на
![]() раз.
раз.

Считаем слева направо -, +, -, +. Сумма переходов равна нулю. Переходы справа от точки (-1,j0) не считаем. Замкнутая система будет устойчива, если m1=0 (в разомкнутой системе все корни левые).
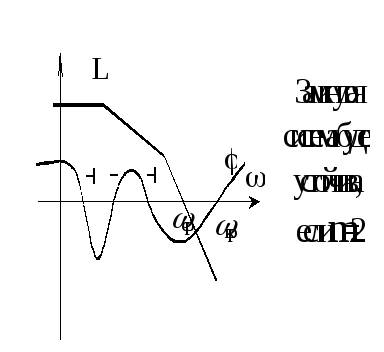
Логарифмический критерий устойчивости (Найквиста)
Это разновидность частотного критерия Найквиста, позволяющего выяснить устойчивость системы по логарифмическим частотным характеристикам разомкнутой системы.
Для устойчивости замкнутой системы, устойчивой в разомкнутом состоянии (или нейтральной), необходимо и достаточно, чтобы критическая частота, соответствующая переходу ЛФХ через линию (-1800) была больше, чем частота среза.



Общая формулировка логарифмического критерия:
Для устойчивости
замкнутой системы необходимо и достаточно,
чтобы разность между числом положительных
и отрицательных переходов кривой
![]() линии
линии![]() в области
в области![]() равнялась
равнялась![]() ,
где
,
где![]() - число правых корней разомкнутой
системы.
- число правых корней разомкнутой
системы.
О применении критериев устойчивости
Если имеется
дифференциальное уравнение системы в
канонической форме или операторное
уравнение вида
![]() ,
(
,
(![]() ),
то в этом случае предпочтительно
использовать алгебраические критерии.
Если порядок уравнения
),
то в этом случае предпочтительно
использовать алгебраические критерии.
Если порядок уравнения
![]() ,
то лучше критерий Гурвица. Кроме того
критерий Гурвица можно рекомендовать,
когда необходимо решить задачу нахождения
границы устойчивости. Для этого
приравнивают к нулю минор
,
то лучше критерий Гурвица. Кроме того
критерий Гурвица можно рекомендовать,
когда необходимо решить задачу нахождения
границы устойчивости. Для этого
приравнивают к нулю минор
![]() и находят из данного уравнения
граничные условия.
и находят из данного уравнения
граничные условия.
Если
![]() ,
то лучше применять критерий Раусса.
,
то лучше применять критерий Раусса.
Частотные критерии предпочтительнее, когда имеются соответствующие частотные характеристики. Частотные характеристики применяются при исследовании систем, которые невозможно описать дифференциальными уравнениями (черный ящик).
