Лекции по теории механизмов и машин

где - коэффициент потерь энергии.

Если 0 , т.е. AД АВ.С ., это значит, что движение машины возможно, но полезная работа не совершается, движение происходит вхолостую.

По величине КПД сравнивают достоинства однотипных машин, например, двигателей внутреннего сгорания, турбин. Чем больше КПД, тем эффективнее машина при прочих равных условиях.

Сравнение эффективности механизмов, кинематических соединений и пар в ряде случаев более наглядно не по КПД, а по коэффициенту потерь .Коэффициент потерь характеризует затраты энергии в машине на преодоление сил вредного сопротивления.

Чем меньше в механизме работа, затрачиваемая на преодоление сил вредного сопротивления, тем меньше коэффициент потерь механизма , тем больше его механический коэффициент полезного действия , тем совершеннее механизм в энергетическом отношении.

При сравнении коэффициентов потерь становится более очевидными недостатки отдельных механизмов или их кинематических пар.

Пример. Сравним, какой механизм является более выгодным в энергетическом отношении. Рядовой зубчатый механизм или червячный механизм.

Зубч. 0,97,

Известно, что Черв. 0,8.

Тогда Зубч. 0,97 1,21 .

Черв. 0,8

Вычислим: Зубч. 1 3 1 0,97 0,03,Черв. 1 4 1 0,80 0,20.

71

Тогда Черв. 0,20 6,7 .

Зубч. 0,03

Отсюда видно, что коэффициент потерь в червячном механизме почти в 7 раз больше, чем в зубчатом механизме).

Это отношение убедительно показывает преимущества зубчатого механизма перед червячным по энергетическим затратам.

5. Колебания скорости машины. Коэффициент неравномерности

хода

Истинная угловая скорость машины в период установившегося движения не остается постоянной, а меняется периодически, принимая одинаковые значения в начале и в конце цикла.

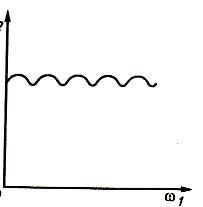
Рассмотрим режим циклической установки движения. Колебания скорости могут достигать какой-то max или min (см. рисунок 2).

Колебания скорости ведущего звена приводят к дополнительным динамическим нагрузкам в кинематических парах, что вызывает вибрации, шум, толчки, которые снижают надежность и долговечность машин.

Чем меньше разница между мгновенными максимальным max и минимальным min

значениями скорости машины, тем более равномерное движение совершает ведущее звено,

тем более в оптимальных условиях работает машина.

Введем понятие средней скорости за цикл ср. :

ср max min .

2

Неравномерность движения машины в период установившегося движения характеризуется коэффициентом неравномерности хода машины, который характеризует колебания скорости относительно средней скорости:

Для каждого типа машины установлены практикой допускаемые значения коэффициентов неравномерности хода:

251 ... 501 - для металлорежущих станков;

501 ...1001 - для прядильных машин;

1001 ... 2001 - для дизельных двигателей;

72

Пример.

Выясним, на сколько процентов max или min отличаются от ср при заданном значении .

Дано:

251 - для металлообрабатывающих станков;

n 400 об мин - скорость вращения ведущего звена.

Тогда ср n 3,14 400 41,89 c 1 30 30

max -?

min - ?

Решение:

Разница составляет 2% от ср .

73

6. Назначение маховика

Чтобы движение машины стало более равномерным т.е. чтобы уменьшить коэффициент , надо увеличить массу звеньев, связанных с главным валом машины на величину m0 , что приведет к увеличению кинетической энергии механизма на величину T0 .

Увеличения массы звеньев добиваются посадкой, как правило, на главный вал машины дополнительной детали – маховика.

Маховик – это массивная деталь, выполненная в форме обода со спицами или сплошного диска. Маховик выполняет роль аккумулятора кинетической энергии. В фазы цикла, когда скорость машины возрастает, маховые массы накапливают кинетическую энергию. И, наоборот, в фазы цикла, когда движение замедляется, они отдают накопленную энергию, препятствуя снижению скорости.

Особенно большое значение имеет маховик в машинах, работающих с резко возрастающей нагрузкой (прессах, дробилках, двигателях автомобилей и тракторов и др.)

Таким образом, основное назначение маховика – это регулирование скорости

машины в период установившегося движения.

Регулирование скорости машины в период установившегося движения заключается в подборе такого соотношения между массой звеньев механизма и действующими силами,

чтобы коэффициент неравномерности хода не превышал заданного допустимого значения.

Чтобы выбрать маховик, надо знать момент инерции маховика Jm или mM .

Существуют разные методы для определения момента инерции маховика.

74

Лекция 11

МЕХАНИЗМЫ С ВЫСШИМИ КИНЕМАТИЧЕСКИМИ ПАРАМИ И ИХ КЛАССИФИКАЦИЯ

Кмеханизмам с высшими кинематическими парами относятся любые механизмы в состав которых входит хотя бы одна высшая пара. Простейший типовой механизм с высшей парой состоит из двух подвижных звеньев, образующих между собой высшую кинематическую пару, а со стойкой низшие (вращательные или поступательные) пары.

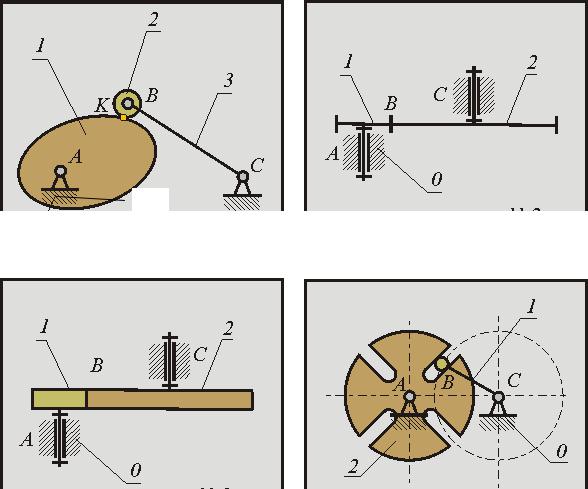
Кпростейшим механизмам с высшей парой относятся :

фрикционные передачи (рисунок 1),

зубчатые передачи (рисунок 2),

кулачковые механизмы (рисунок 3),

поводковые механизмы (в том числе и мальтийские - рисунок 4).

Структурные схемы простейших механизмов с высшими КП

0

75

Фрикционными механизмами или передачами сцепления называются механизмы с высшей парой, в которых передача движения в высшей паре осуществляется за счет сил сцепления или трения в зоне контакта.

Кулачковым механизмом называется механизм с высшей парой, ведущее звено которого выполнено в форме замкнутой криволинейной поверхности и называется кулачком

(или кулаком).

Зубчатыми механизмами называются механизмы, звенья которых снабжены зубьями

(зубчатый механизм можно определить как многократный кулачковый, рассматривая зацепление каждой пары зубьев, как зацепление двух кулачков). Рабочие поверхности зубьев должны быть выполнены так, чтобы обеспечивать передачу и преобразование движения по заданному закону за счет их зацепления. Условия, которым должны удовлетворять рабочие поверхности высших пар, формулируются в разделе теории механизмов - теории зацепления или теории высшей пары.

ЗУБЧАТЫЕ МЕХАНИЗМЫ

ОСНОВНАЯ ТЕОРЕМА ЗАЦЕПЛЕНИЯ

На первый взгляд кажется, что расположение любого профиля зубьев по цилиндрической поверхности колес обеспечит постоянное передаточное отношение. Однако это не так. График i12 (ω1) при произвольной форме профилей зубьев представляет собой некоторую волнистую линию в соответствии с рисунком 5. Такое даже незначительное колебание передаточного отношения приводит к ударам зубьев.

i1 2

Рисунок 5

Основная теорема зацепления (теорема Виллиса) устанавливает требование к боковым профилям зубьев цилиндрических колес для обеспечения строго постоянного передаточного отношения, т.е. обеспечения нормального зацепления в течение полного оборота ведущего звена.

76

Рассмотрим на рисунке 6 зацепление зубьев двух профилей, где а-а – профиль ведущего звена 1, вращающегося со скоростью ω1, b-b – профиль ведомого звена 2,

вращающегося со скоростью ω2.

Окружные скорости точки М каждого из колес:

v1 1 O1M ; v2 2 O2 M.

Через точку М проводим нормаль NN и касательную ТТ и проецируем на них скорости v1 и v2 (векторы скоростей построены перпендикулярно отрезкам O1M и O2M) . Проекции

скоростей v1 и v2 на касательную ТТ не равны между собой, что свидетельствует о наличии

скольжения между профилями. Проекции же v1n и v2n на нормаль NN непременно должны

быть равны между собой, т.е. v1n = v2n .

Действительно, если v1n > v2n , то профиль первого зуба внедрится в профиль второго,

если же v1n < v2n , то произойдет сцепление профилей. Оба явления при нормальном сцеплении неприемлемы.

Рисунок 6

77

Опустим перпендикуляры из центров О1 и О2 на нормаль NN и рассмотрим

треугольники O1N1M и M v1n v1 . Стороны этих прямоугольников взаимно перпендикулярны,

поэтому треугольники подобны. Из их подобия следует:

v1n O1N1 , v1 O1M

откуда

Рассматривая подобные (вследствие равенства углов) треугольники O1N1Р и O2N2Р,

получаем отношение

Подставив соотношение (2) в уравнение (1), находим

Уравнение (3) выражает смысл основной теоремы зацепления: для обеспечения

постоянного заданного отношения угловых скоростей общая нормаль NN к

сопряженным профилям зубьев в точке касания делит линию центров О1О2 в точке Р на части, обратно пропорциональные угловым скоростям.

Анализируя уравнение (3), можно сделать вывод: для обеспечения постоянного

передаточного отношения при заданном межосевом расстоянии О1О2 отношение O2 P

O1P

78

должно быть постоянным, т.е. точка Р должна занимать неподвижное положение на линии центров колес.

Если это условие выполняется, то окружности радиусов rw1 и rw2 , проведенные из центров О1 и О2, при работе механизма будут катиться одна по другой без скольжения.

Полюсом зацепления называется точка Р пересечения общей нормали к профилям с

линией центров О1О2.

Начальными окружностями зубчатых колес называются окружности радиусов rw1

, то есть окружности колес, касающиеся в полюсе P.

Таким образом, чтобы в зацеплении выполнялась теорема зацепления, профили зубьев должны очерчиваться по взаимоогибающим кривым. Среди кривых, отвечающих требованию основной теоремы зацепления, наиболее распространена эвольвента.

Зацепление, у которого профили зубьев выполнены по эвольвенте, называют эвольвентным зацеплением.

Преимущества эвольвентного зацепления:

1)простота изготовления, причем оба колеса, входящие в зацепление, могут быть изготовлены одним и тем же инструментом;

2)плавность и незначительный шум в работе;

3)при монтаже допускается погрешность в межосевом расстоянии;

4)высокая прочность зубьев при изгибе, так как их толщина увеличивается от вершины к основанию;

5)при равномерном вращении колес точка контакта перемещается равномерно по прямой линии, что обеспечивает плавность передачи усилия в одном направлении.

Недостатки эвольвентного зацепления:

1)касательные составляющие скоростей (проекции v1 и v2 на рисунке 6) не равны по значению, поэтому наряду с перекатыванием профилей происходит их проскальзывание, вызывающее трение скольжения и повышенный износ профилей;

2)имеет место неравномерность скольжения в зоне контакта зубьев, что служит причиной неравномерного износа зубьев вдоль боковых поверхностей,

вызывающего искажение эвольвентного профиля,отсюда, нарушение основной теоремы зацепления и, как следствие, удары зубьев;

79

3)прочность зубьев внешнего зацепления в зоне контакта мала ввиду соприкасания выпуклых поверхностей.

ОСНОВНЫЕ ЭЛЕМЕНТЫ ЦИЛИНДРИЧЕСКИХ НОРМАЛЬНЫХ КОЛЕС

На основные параметры зубчатых колес стандартом установлены определенные нормы.

Нормальными колесами, или нулевыми называют колеса, изготовленные в соответствии с этими нормами. Рассмотрим сечение части колеса плоскостью,

перпендикулярной оси вращения, в соответствии с рисунком 7.

Рисунок 7

Шагом зубчатого колеса называется расстояние между одноименными точками двух соседних зубьев, измеренное по дуге окружности. Естественно, что шаг, измеренный по той

или иной окружности, будет различным.

Делительной окружностью называется окружность, по которой шаг равен