Лекции по теории механизмов и машин

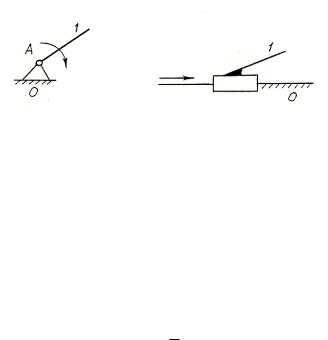
Лекция 3

СТРУКТУРА МЕХАНИЗМОВ

Удобная классификация плоских механизмов была разработана профессором Л.В.

Ассуром и опубликована в 1916 году. Дальнейшее развитие она получила в трудах академика И.И. Артоболевского.

Втаблице 1 показаны основные условные обозначения звеньев и кинематических пар

вплоских механизмах.

Основной принцип образования механизмов заключается в последовательном присоединении к механизму первого класса (или к механизмам первого класса) структурных групп Ассура с нулевой степенью подвижности.

Класс механизма определяется классом высшей по классу группы Ассура, входящей в механизм. Большинство механизмов являются механизмами второго класса.

Механизмом первого класса называется ведущее звено, соединенное кинематической парой (вращательной или поступательной) со стойкой (рисунок 1).

Рисунок 1

Группой Ассура называется простейшая открытая кинематическая цепь, степень подвижности которой равна нулю и которая не может распадаться на более простые кинематические цепи с нулевой степенью подвижности.

Степень подвижности группы Ассура

WГР 3 n 2 p5 0

или

p5 32 n .

Возможны следующие сочетания чисел звеньев и пар структурных групп: n = 2,4,6,8,…

p5 = 3,6,9,12,…

В зависимости от сочетания чисел звеньев и пар различают группы Ассура второго,

третьего, четвертого и т.д. классов. В зависимости от сочетания вращательных и

21

поступательных пар и их взаимного расположения группы Ассура второго класса делятся на пять видов.

Для групп Ассура II класса имеем: n 2 ; p5 3 ,

где n –число звеньев группы; p5 – число пар V класса.

Это простейшее сочетание чисел звеньев и пар в группе, удовлетворяющее условию p5 32 n . Значит, группа, имеющая два звена и три пары V класса, называется группой II

класса второго порядка.

Группа Ассура III класса третьего порядка – это группа, имеющая четыре звена и шесть пар V класса, т.е. n 4 ; p5 6 .

Отличительной особенностью групп III класса является наличие базисного звена.

Группа Ассура третьего класса показана на рисунке 3.2.

Такое же число звеньев и пар ( n 4 ; p5 6 ) содержит группа Ассура IV класса, но ее отличительной особенностью является наличие двух базисных звеньев (2, 4) и

четырехстороннего замкнутого подвижного контура (BCEF).

Порядок структурной группы Ассура определяется числом свободных элементов звеньев, которыми она присоединяется к механизму.

Группы II класса могут быть только группами второго порядка (двухповодковыми),

т.е. число элементов, которыми каждая группа присоединена к ведущему звену и стойке, не может быть меньше двух.

Втаблице 2 приведены некоторые схемы групп Ассура с указанием их класса и порядка, а также виды групп Ассура второго класса.

Вплоских механизмах, кроме низших пар могут быть и высшие. При структурном анализе каждую высшую пару необходимо заменить кинематической цепью, состоящей только из низших пар.

Иногда при конструктивном оформлении в схему механизма вводят звенья, которые формально изменяют степень подвижности, но фактически не влияют на кинематику всего звена. Такие звенья и кинематические пары, в которые входят звенья, являются пассивными

(лишними) условиями связи. Общих методов отыскания лишних степеней подвижности и пассивных условий связи нет, поэтому приходится полагаться на личный опыт,

приобретаемый при изучении курса теории механизмов и машин. При анализе механизма необходимо найти и устранить пассивные условия связи.

22

Таблица 1 – Основные условные обозначения звеньев и кинематических пар в плоских механизмах

Звено входящее в две вращательные пары

Звено, входящее в три вращательные пары, лежащие на одной прямой

Звено, входящее в три вращательные пары, не лежащие на одной прямой

Поступательная пара:

Оба звена подвижные

Одно звено подвижное

Вращательная пара:

Оба звена подвижные

Одно звено неподвижное

Пара четвертого класса (высшая)

23

Таблица 2 – Некоторые схемы групп Ассура

2-й вид

3-й вид

4-й вид

5-й вид

24

Последовательность структурного анализа механизма

Порядок расчленения механизма на группы будет обратным порядку присоединения групп к механизму (механизмам) первого класса. Поэтому при расчленении механизма на структурные группы вначале устанавливают ведущее звено, а затем удаляют группы второго класса, сначала наиболее удаленные от начальных (ведущих) звеньев. При невозможности удаления групп второго класса, удаляют группы Ассура более высоких классов, сначала третьего, а затем четвертого класса. После такого удаления групп в механизме должны остаться только механизмы первого класса.

Последовательность структурного анализа механизмов следующая:

1)найти и устранить пассивные условия связи;

2)определить степень подвижности механизма;

3)выбрать начальное (ведущее) звено;

4)заменить высшую пару кинематической цепью, состоящей только из низших пар;

5)расчленить механизм на группы Ассура;

6)записать формулу строения механизма;

7)определить класс механизма.

25

Лекция 4

Примеры структурного анализа механизма

ПРИМЕР 1: Произвести структурный анализ механизма приемника давления электрического дистанционного манометра (рисунок 2).

РЕШЕНИЕ: Степень подвижности механизма W определяем по формуле Чебышева.

W 3 n 2 p5 p4 ,

где n – число подвижных звеньев;

p5 – число кинематических пар 5-го класса; p4 – число кинематических пар 4-го класса.

Арабскими цифрами на схеме (рисунок 2) обозначены звенья механизма, а именно:

1 – ползун; 2 – коромысло (звено BCD); 3 – шатун; 4 – ползун.

Итого, число подвижных звеньев n = 4.

Анализ кинематических пар, обозначенных на схеме большими буквами латинского алфавита, сведен в таблицу 1.

Таким образом, число кинематических пар 5-го класса p5 равно пяти, а число пар 4-го класса p4 равно одному.

В механизме отсутствуют пассивные связи и звенья, вносящие лишние степени свободы. Степень подвижности механизма по формуле (1):

W 3 4 2 5 1 1

Ведущее звено задано в условии примера, и оно должно быть одно, так как W = 1.

Рисунок 2

Таблица 3 - Анализ кинематических пар механизма

26

Структурный анализ по Ассуру-Артоболевскому выполняется для кинематической цепи, состоящей только из кинематических пар 5-го класса. Если же исследуемый механизм имеет кинематические пары 4-го класса, то они предварительно должны быть заменены одним звеном, входящим в две кинематические пары 5-го класса. Получившийся после такой замены механизм называется заменяющим.

Схема заменяющего механизма представлена на рисунке 3. Дополнительное звено 5 –

ползун. Анализ кинематических пар заменяющего механизма сведен в таблицу 2.

Рисунок 3

Степень подвижности заменяющего механизма определяется подстановкой в формулу Чебышева следующих значений: n = 5, p5 = 7.

Тогда

W 3 5 2 7 1

Таким образом, степень подвижности осталась равной единице, т.е. замена произведена верно.

27

Следующим этапом структурного анализа является выделение из механизма

структурных групп с нулевой степенью подвижности.

Эту задачу рекомендуется решать по следующей методике:

1)Отсоединение структурных групп начинать с групп II класса и наиболее удаленных по кинематической цепи от ведущего звена;

2)Если степень подвижности оставшейся кинематической цепи изменилась, то отсоединение сделано неверно, и следует отсоединить пару звеньев в другой комбинации;

3)Если отсоединить группу II класса не удается, то следует рассмотреть возможности отсоединения группы III класса;

4)После отсоединения первой группы отсоединить от оставшейся кинематической цепи следующую группу и т.д. до тех пор, пока не останется механизм I класса, т.е. ведущее звено, соединенное кинематической парой со стойкой.

Рассмотрим изложенную последовательность на примере заменяющего механизма.

Вначале отделяется группа Ассура второго класса, образованная звеньями 4 и 3 (рисунок

4,а), а затем группа второго класса, состоящая из звеньев 2 и 5 (рисунок 4,б).

На этом расчленение механизма заканчивается, так как остались ведущее звено 1 и

стойка 0, т.е. механизм I класса (рисунок 4,в).

Разложение механизма на группы Ассура и структурные формулы приведены на рисунке 4.

Структурный анализ показал, что механизм имеет одну степень свободы и

структурная формула механизма запишется в виде

I (0, 1) → II2 (5, 2) → II2 (3, 4) .

Римские цифры показывают класс структурных групп, а индексы, обозначенные арабскими цифрами, вид групп.

28

Класс механизма определяется наивысшим классом структурной группы Ассура,

входящей в состав механизма. Для исследуемого механизма наивысший класс присоединенных групп – второй, поэтому весь механизм относится ко II классу (при ведущем звене 1).

а)

II2(3, 4)

б)

II2(5, 2)

в)

I (0, 1)

Рисунок 4 - Структурные составляющие механизма:

а) группа Ассура II класса 2-го вида; б) группа Ассура II класса 2-го вида;

в) механизм I класса

29

ПРИМЕР 2: Определить класс механизма и записать структурную формулу механизма

(рисунок 5).

Рассмотрим кинематическую схему механизма на рисунке 5.

Рисунок 5 – Кинематическая схема механизма

1)Проведем структурный анализ механизма. Пронумеруем все подвижные звенья

иклассы кинематических пар, как это показано на рисунке 5. Подсчитываем степень подвижности механизма по формуле Чебышева:

W 3 n 2 p5 p4 ,

где n = 14; p5 = 20.

Отсюда,

W 3 14 2 20 2 .

Значит механизм имеет два ведущих звена, которым должны быть заданы два независимых движения. Выбираем за ведущие звенья 1 и 12.

2) Расчленяем схему механизма на группы Ассура. Каждую группу Ассура изображаем отдельно, как показано на рисунке 6. Наиболее удаленными от начальных звеньев 1 и 12 являются звенья 2, 3, 4, 5 с кинематическими парами А, В, С, D, Е, F. Это группа Ассура Ш класса.

Если бы мы попытаемся отделить звенья 4 и 3, то после их отделения в оставшейся схеме остается одинокое, "болтающееся", звено 5. А при попытке отделить звенья 3, 5 –

остается свободным звено 4, чего не должно быть.

30