
Чистяков Ч2
.pdf3. Высокочастотный пробой газа и сформировавшийся разряд
При известных условиях, амплитуде поля E0 , частоте ω и давлении газа р происходит высокочастотный пробой газа, т.е. переход из состояния газа, являющегося хорошим изолятором, к состоянию, когда газ обладает хорошей электропроводностью как при высокочастотном, так и при постоянном напряжении. Конечное состояние объема газа, находящегося Е поле высокой частоты, представляет собой обычно плазму со всеми присущими ей особенностями.
Подобно тому как соотношение (88) (Конспект лекций, Ч. 1) является условием пробоя на постоянном напряжении, при высокочастотном также имеются свои условия пробоя. Однако очевидно, что здесь картина пробоя будет сильно изменяться в зависимости от соотношения частоты столкновений электронов с молекулами газа ν и частоты поля ω. Если ν >> ω, то в процессе увеличения концентрации электронов и ионов при пробое, по-видимому, играют роль незавершенные электронные лавины, направление движения которых изменяется при изменении направления поля. Однако с понижением частоты столкновений ν из-за понижения давления газа или с увеличением частоты поля роль этих незавершенных лавин уменьшается и при ν ≤ ω эти лавины отсутствуют. Здесь приобретают значение новые процессы в особенности накопление энергии электронами благодаря столкновениям. В оптимальном случае это выглядит следующим образом; электрон на длине свободного пробега увеличивал свою энергию, но после столкновения на правление его скорости изменилось; если это совпало с изменение знака поля, то и в течение второго полупериода электрон будет ускоряться, далее снова упругое столкновение с изменением направления движения, вновь изменение направления поля, сопровождающееся ускорением электронами т.д. Известная часть электронов при ν ~ ω накапливает энергию подобным об разом до тех пор, пока не произведут возбуждение или ионизацию. Если процесс ионизации будет преобладать над рекомбинацией в объеме газа и на поверхности оболочки прибора, то постепенно сформируется плазма, составляющая основу высокочастотного разряда.
Существующие теории высокочастотного пробоя газа охватывают лишь частные случаи этой многообразной и сложной проблемы.
Одна из теорий построена для области низких давлений газа и основывается на уравнениях (46) и (47). Влияние обычных зарядов не учитывается. Введен следующий критерий пробоя: на длине свободного пробега электрон должен приобрести энергию равную энергии ионизации молекул газа eUi.
Если использовать этот критерий и уравнения (46) и (47) то при пробое должны
61

быть выполнены следующие два условия: |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
u = 2 |
e |
Ui = eE0 (1− cosωt), |
(63) |
|||||
m |
||||||||
|
|
|
|
mω |
|
|||
λ = |
eE0 |
(ωt − sin ωt). |
(64) |
|||||
2 |
||||||||
|
mω |
|
|
|
||||
Здесь взято для упрощения θ = 0 |
и |
u0 = 0. Уравнения (63) и (64) связывают |
||||||
величины E0, ω, λ и t; если исключить |
t, |
то можно найти зависимость |
E0 = f1(ω) |
|||||
для данной величины λ, которая характеризует природу газа и его давление. Зависимости амплитуды поля при высокочастотном пробое от его частоты для
различных давлений аргона показаны на рис. 24. При увеличении давления E0, соответствующая минимуму, увеличивается и сдвигается в сторону больших частот.
Из кривых, показанных на рис. 24, можно получить зависимости E0 = f2( p) при ω = const , которые показаны на pис. 25.
Экспериментальная проверка этих расчетных кривых показала качественное, а в некоторых случаях и количественное совпадение результатов для области давлений 10-2 –10-1 мм рт.ст.
Можно построить также зависимость поля при пробое E0 от частоты f и давления газа p, которая представляет собой поверхность в трехмерном пространстве E0, f, p и определить экстремальные точки.
Для средних и высоких давлений хорошо разработана диффузионная теория высокочастотного пробоя. Условия, для которых эта теория справедлива, следующие: средний свободный (пробег электронов и амплитуда их колебаний значительно меньше размеров объема, в котором возникает пробой λe << d если размеры этого объема порядка 10 см, то давление газа должно превосходить10-2 мм рт.ст. а частота поля составлять более 100 МГц. При этих условиях основную роль играют два процесса: ионизация молекул ударами электронов и диффузия электронов к стенкам разрядной камеры. В некоторых газах значительную роль играют отрицательные ионы и, следовательно, нужно учитывать также процесс объемной рекомбинации ионов с ионами.
62
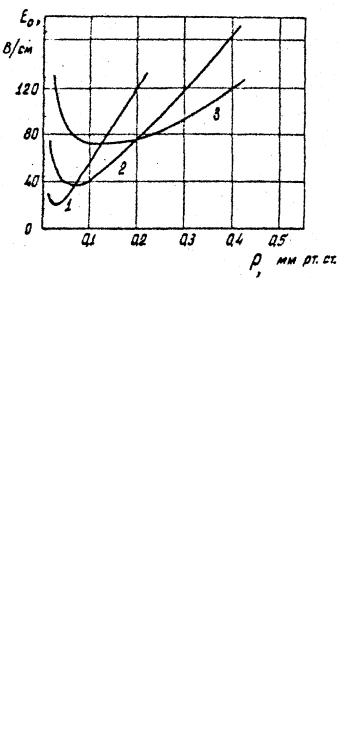
Рис. 24. Зависимость амплитуды поля при пробое E0 от частоты при различных давленичх аргона: 1–1,5·10-2; 2–6·10-2; 3–12·10-2 мм рт.ст.
Рис. 25. E0 = f2(p) при высокочастотном пробое в аргоне: 1 - 40 МГц; 2 - 100 МГц; 3 - 180 МГц
63

В случае высокой концентрации заряженных частиц в высокочастотном разряде начинают играть роль ступенчатые процессы, а также рекомбинация ион-электрон при тройных столкновениях. Однако в случае пробоя, когда концентрация электронов и ионов еще невелика, эти дополнительные процессы можно в большинстве случаев не учитывать и ограничиться первыми двумя процессами, что позволяет относительно несложно построить диффузионную теорию высокочастотного пробоя.
Рассмотрим газ, находящийся между бесконечными параллельными пластинами с расстоянием d между ними, в котором под действием внешнего излучения равномерно по всему объему создается N0 электронов и ионов в 1 см3 в 1 с. Кроме этого, за счет высокочастотного поля электроны производят ионизацию с частотой νи,
таким образом, скорость возникновения новых электронов в 1 см3 составляет
и = νиne . Электроны и ионы движутся к ограничивающим поверхностям за счет диффузии, поток диффундирующих частиц дается обычным выражением
De (div grad ne ) .
Используя уравнение непрерывности, записываем увеличение плотности электронов в стадии нарастания высокочастотного тока
∂n |
|
|
|
|
∂2n |
|
||
e |
= N |
|
+ ν |
n + D |
e |
, |
(65) |
|
|
|
|
||||||
∂t |
0 |
|
и e |
e |
∂x2 |
|
||
где ne зависит от времени и координат. Для самостоятельного разряда N0 - малая величина. Скорость изменения концентрации при пробое также может быть очень малой или равной нулю, при этом устанавливается самостоятельный разряд с не высокой концентрацией заряженных частиц. Уравнение (65) упрощается
∂2n |
ν |
n |
|
||
e + |
|
и |
e |
= 0. |
(66) |
De |
|
||||
∂x2 |
|
|
|
||
Если выбрать начало координат в центре между электронами - стенками и предположить, что у стенок плотность электронов спадает до нуля, то можно получить решение уравнения (66)
|
n |
= C cos |
|
νи |
|
x ; |
|
|
|||||
|
e |
1 |
|
De |
||
|
|
|
|
|||
при x = 0 |
ne = ne0 = С1; |
|
|
|
||
n |
= n |
cos |
|
νи |
|
x . |
(67) |
|
|||||||
e |
e0 |
|
|
De |
|
||
|
|
|
|
|
|||
Получили распределение концентрации электронов в промежутке. Условие, при
64

котором разряд будет самостоятельным, получим из следующего граничного условия: у
поверхности электродов |
|
n |
= 0 |
и |
аргумент функции (67) составит |
± π |
|||||||
|
|
|
|
e |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(отрицательные значения |
ne |
не имеют смысла). |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда получаем |
|
νи |
|
d |
= |
π |
или |
|
|
|
|
||
|
De 2 |
2 |
|
|
|
|
|||||||
|
|
|
|
|
|
D |
π |
2 = ν |
и |
, |
(68) |
||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
e |
|
|
|
||||
|
|
|
|
|
|
|
d |
|
|
|
|
||
что и является условием самостоятельности разряда при взятых исходных предпосылках.
Уравнение (68) связывает размеры промежутка d с давлением и природой газа (νи, De ), и из этого уравнения может быть получена амплитуда высокочастотного поля при про бое E0 в зависимости от всех этих условий.
Расчет является сложным и может быть выполнен, если заранее известна |
|
функция распределения электронов по скоростям в высокочастотном разряде, после |
|
чего можно использовать соотношение (39). (Конспект лекций. Ч. 1, гл. III, |
z = νи ) |
Подобные расчеты и были произведены не только для рассмотренного промежутка с |
|
плоскими параллельными ограничивающими поверхностями, но и для других форм |
|
разрядных пространств, и результаты расчетов хорошо совпали с |
данными |
экспериментов [27]. На рис. 26 показана типичная зависимость E0 при пробое от давления газа p. Наличие минимума объясняется тем, что при малых давлениях электрическое поле при пробое E0 увеличивается из-за того, что необходима усиленная ионизация для компенсации возрастающих потерь электронов на стенки в результате диффузии. При больших давлениях E0 увеличивается, так как необходимо компенсировать возрастающие потери энергии электронов на упругие удары. При не которых средних условиях (р ~ 1 мм рт.ст.) E0 имеет минимальное значение.
65
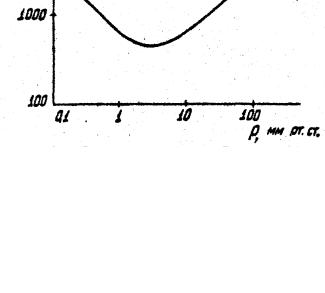
Рис. 26 Зависимость E0 = f(p) согласно диффузионной теории
(средние и высокие давления газа)
66
Напряжения, необходимые для поддержания сформировавшегося высокочастотного разряда, значительно меньше потенциалов пробоя. Причиной этого является появление пространственного заряда положительных ионов, который уменьшает потери электронов на стенках в результате диффузии при этом свободная диффузия электронов переходит в амбиполярную (двуполярную). Так как Da << De
(Конспект лекций. Ч. 1, гл.III) то чтобы компенсировать потери электронов при этом виде диффузии, требуется меньшая скорость образования электронов в разряде, а следовательно, меньшее электрическое поле и общее приложенное напряжение.
Минимальное напряжение горения может быть очень низким, в некоторых случаях меньшим потенциала ионизации Ui . Это явление объясняется механизмом накопления энергии электронами из-за соударений.
В основу теории сформировавшегося высокочастотного разряда берется то же уравнение, что и для теории пробоя, однако при этом учитывается образование в промежутке плотного заряда положительных ионов, и в связи с этим изменение характера диффузии электронов к стенкам. Это уравнение следующее:
|
|
|
|
|
Da div grad ne + νиne = 0 , |
(69) |
где D = |
µeD+ + µ+De |
|
µ+ |
D – коэффициент амбиполярной диффузии. |
||
|
|
|||||
a |
|
µ+ + µe |
|
e |
|
|
|
|
µe |
|
|||
|
Если уравнение (69) применить к высокочастотному раз ряду в цилиндрической |
|||||
трубе при давлениях, когда имеют место диффузионные процессы |
( ν >> ω , λe << R ), |
|||||
то получается дифференциальное уравнение и его решение такого же типа, как и для столба тлеющего разряда на постоянном токе. И в этом случае в итоге расчета можно получить зависимость E/p = f(pR) [уравнение (19)].
Было замечено, что в сформировавшемся высокочастотном разряде из-за ухода электронов на стенки образуется пространственный положительный заряд, создающий статические электрические поля и потенциалы, которые для центральной; области разряда относительно граничной области (или электродов) могут составлять до несколько сотен вольт. В связи с этим можно объяснить наблюдаемое в некоторых случаях явление распыления материала электродов в высокочастотном разряде при низких давлениях газа, которое таким образом, подобно катодному распылению на постоянном токе тлеющего раз ряда.
Измерение параметров ne и Te плазмы и области пространственного заряда для высокочастотных разрядов производилось методом двойного плавающего зонда [28]. Отметим некоторые результаты, полученные этим методом: при высокочастотных
67
токах порядка миллиампер концентрация электронов составляет около |
109 см-3, |
а |
средние энергии при условии значительных давлений газа ν > ω |
составляли |
|
несколько электронвольт. В некоторых работах была получена малая зависимость |
Te |
|
от ne , например, при разряде в воздухе и изменении давления от 0,1 до 11 мм рт.ст. ( f = 108 Гц), температура электронов оставалась около 3 104 К при изменении ne от
1010 до 1012 см-3. В ряде случаев было найдено максвелловское распределение электронов по скоростям.
Высокочастотный разряд является интенсивным источником положительных ионов, которые можно использовать в ускорителях заряженных частиц. Для создания источника ионов чаше используется кольцевой безэлектродный высокочастотный разряд (Н – разряд) [29].
4. Высокочастотный разряд в вакууме
4.1. Резонансный разряд, вызванный вторичной эмиссией (мультипакторный разряд)
Для возникновения этого вида разряда должны быть выполнены два условия. Во - первых, коэффициент вторичной эмиссии материала стенок или электродов должен быть более единицы σ > 1. Электроны под действием высокочастотного поля движутся в прямом и обратном направлении и сталкиваются с противоположными стенками или электродами, вызывая выход вторичных электронов. В том случае, когда эти столкновения и выход вторичных электронов совпадают по времени с переменой знака поля и время пролета вторичных электронов до противоположной стенки будет равно полупериоду высокочастотного напряжения, будет происходить умножение числа электронов от одного полупериода поля к другому или за нечетное число полупериодов. Это – второе условие возникновения разряда.
При возрастании тока электронов в вакуумном промежутке формируется объемный заряд, который ограничивает увеличение тока и создает его насыщение.
Рассмотрим элементарную теорию этого разряда для системы плоских и параллельных электродов (или стенок) и малой плотности тока, что позволяет пренебречь влиянием объемных зарядов. За основу возьмем уравнения (46) для скорости и (47) для координат электрона, движущегося без столкновений с молекулами
газа.
68
Пусть |
t = 0 |
u = u0 , где |
u0 |
- скорость электрона при выходе из |
ограничивающей стенки или электрода при |
x = 0 . В этом случае предполагая - что |
|||
имеет место резонанс, о котором сказано выше, и время движения электрона между
противолежащими поверхностями, |
находящимися |
на |
расстоянии |
d, кратно |
|||||||
полупериоду высокочастотного напряжения, т.е. t = Tn |
= nπ |
(n =1, 3, 5, …), получаем: |
|||||||||
|
|
|
|
|
|
2 |
ω |
|
|
||
u = u + 2eE0 cosθ , |
|
|
|
(70) |
|||||||
|
|
|
0 |
|
mω |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
где Ө - фаза вылета электронов, а для d имеем: |
|
|
|
|
|||||||
d = u 0πn |
+ |
eE0 |
(πncosθ + 2sin θ) . |
(71) |
|||||||
mω2 |
|||||||||||
ω |
|
|
|
|
|
|
|||||
Из уравнения (71) получаем выражение для E0 |
|
|
|
|
|||||||
E0 = |
|
|
|
ω2d − u0πωn |
|
. |
(72) |
||||
|
e |
(πncosθ + 2sin θ) |
|||||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
m |
|
|
|
|
|
||
Допустим, что отношение скорости первичных электронов, попадающих на электрод u к начальной скорости вторичных электронов u0, постоянно. Данное допущение недостаточно обосновано, но облегчает решение задачи и приводит к хорошему согласию теории и эксперимента.
Обозначая |
u |
= K , преобразуем выражения (70) и (72) |
|
|||||||||||||||
|
|
|||||||||||||||||
|
u0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u = |
K |
|
2eE0 cosθ |
; |
|
|
(73) |
||||||
|
|
|
|
|
K −1 |
mω |
|
|
||||||||||
|
|
E0 |
= |
|
|
|
|
|
|
|
|
|
ω2d |
|
. |
(74) |
||
|
|
|
e |
|
|
|
K +1 |
|
|
|
|
|
||||||
|
|
|
|
|
( |
|
|
|
πncosθ + 2sin θ) |
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
m K −1 |
|
|
|
|
|
|
|||||||
или напряжение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U0 |
= |
|
|
|
|
|
|
|
|
|
ω2d2 |
|
|
. |
(75) |
|
|
|
|
e |
|
|
K +1 |
|
|
|
|
||||||||
|
|
|
|
|
( |
|
πncosθ + 2sin θ) |
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
m K −1 |
|
|
|
|
|
|
|||||||
Формулы (74) и (75) дают соответственно величины E0 |
и U0 , при которых, |
|||||||||||||||||
возникает резонансный разряд, если энергия электронов достаточна для получения вторичной эмиссии при σ > 1.
Минимальные значения E0 и U0 получаются при максимуме знаменателя, что достигается при
69
K −1 |
2 |
|
|||
θ = arctg |
|
|
|
. |
(76) |
K +1 |
|
||||
|
πn |
|
|||
На рис. 27 показана расчетная зависимость U0 при пробое от произведения fd. Подобные зависимости для различных значений K и Ө дают совпадение с результатами опытов в пределах 10–20% и могут быть использованы при оценке возникновения разряда в реальных условиях.
Получается целая область сочетаний U0 и f, при которых может существовать разряд. Появление этой области объясняется тем, что начальные фазовые углы выхода электронов могут быть различными. Наличие нижней границы области обусловлено необходимостью возникновения вторичной эмиссии.
Разряд может появляться при напряжениях, начиная с 50–60 В и выше. Рассматриваемый разряд, основанный на вторичной эмиссии (мультипакторный
разряд), может возникать в высокочастотных резонаторах, используемых для ускорения заряженных частиц, линейных ускорителях, циклотронах и т.д. и является в данном случае вредным явлением.
Для устранения этого разряда применяется:
а) подача постоянного напряжения между электродами, что нарушает условия резонанса;
б) выбор соответствующей формы электродов; в) выбор материала поверхностей металлов, которые бы давали σ < 1.
Понижение коэффициента σ может быть достигнуто также очисткой поверхностей металлов, например при тлеющем или высокочастотном разряде в инертном газе или водороде;
г) увеличение рабочего напряжения резонатора до уровня, при котором разряд не может существовать и т.д.
70
