Лабораторные по физике

масштабную сетку выбрать так, чтобы полностью использовалась вся площадь рисунка. Для выбора масштаба времени следует вычислить значение

(Тmax − Тmin) / n, где Тmax и Тmin − наибольшее и наименьшее значения из всех Т1 и Т2, n=10 − число делений на оси Т, и результат округлить до первой значащей цифры слева в сторону завышения. Экспериментальные точки соединить в каждом случае плавной линией, которая должна лежать возможно

ближе к точкам и чтобы по обе стороны линии оказывалось равное их количество.

Таблица 6.3 − Результаты эксперимента

6.6.2.7По точке пересечения полученных кривых T1 = f1 (ℓ) и T2 = f2 (ℓ), соответствующих колебаниям маятника на одной и другой призмах, определить положение чечевицы, которое дает наиболее близкие друг к другу значения периодов.

6.6.2.8Снять маятник и установить чечевицу 7 на найденную графически отметку.

6.6.2.9Для этого положения чечевицы измерить время t ста полных колебаний способами, описанными в п.п. 6.6.2.2 и 6.6.2.3. Измерения производить три раза. Результаты измерений записать в таблицу 6.4.

6.6.2.10По результатам измерений вычислить периоды колебаний Т1 и

Т2 по формуле Т = tср / 100, где tср − среднее значение времени из трех измерений и занести их в таблицу 6.4.

6.6.2.11 Снять маятник с подвеса, положить на призму балансировки и

добиться его уравновешивания. Измерить масштабной линейкой с точ-

ностью до миллиметра расстояние a1 от центра тяжести маятника до расположенной со стороны нониуса опорной призмы. Расстояние от центра тяжести до второй опорной призмы определить по формуле a2 = ℓпр − a1.

Приведенная длина ℓпр указана на установке. Значения a1 и a2 записать в таблицу 6.4.

6.6.2.12По данным таблицы 6.4, пользуясь формулой (6.21), подсчи-

тать ускорение свободного падения g в данной точке.

6.6.2.13Заполнить таблицу 6.5.

71

Таблица 6.4 − Результаты эксперимента

Таблица 6.5 − Абсолютные погрешности отсчета непосредственно измеряемых величин

6.7 Оценка погрешности измерения

6.7.1Для оценки погрешности измерения ускорения свободного падения

применить грубый метод расчета погрешностей [5].

6.7.2Записать рабочую формулу (6.21) и перейти в ней к непосред-

ственно измеряемым величинам (воспользоваться равенствами Т = t / N и

N = N1 = N2).

6.7.3Получить выражение для вычисления относительной погреш-

ности εотн = g / g путем логарифмирования и последующего дифферен-

цирования функции g по параметрам t1, t2, a1 ,a2, считая переменными только

те величины, которые были измерены с известной точностью. Грубые ошиб-

ки исключить из рассмотрения (N = const).

6.7.4Записать полные наименования абсолютных погрешностей изме-

рения, вошедших в выражение относительной погрешности εотн.

6.7.5Вычислить относительную погрешность измерения ускорения свободного падения εотн = g / g, используя данные таблицы 6.4 и 6.5.

6.7.6Подсчитать абсолютную погрешность измерения

g= g εотн.

6.7.7Сравнить экспериментальное значение g с табличным, записать

вывод. Окончательный результат представить в виде g = (g ± g) м/с2.

72

6.8Контрольные вопросы

6.8.1Математический маятник

6.8.1.1Дать определение математического маятника.

6.8.1.2Какие внешние силы действуют на маятник?

6.8.1.3Определить момент силы Р относительно оси 0 (см. рисунок 6.1).

6.8.1.4Каково математическое выражение основного закона вращательного движения?

6.8.1.5Что называется моментом инерции материальной точки?

6.8.1.6Что называется моментом инерции тела? Каков его физический

смысл?

6.8.1.7Записать дифференциальное уравнение колебаний математического маятника и его линейную форму. Почему нужно рассматривать малые углы отклонения маятника?

6.8.1.8Записать кинематическое уравнение гармонического колебания.

6.8.1.9Дать определения периода, амплитуды, частоты, фазы колеба-

ния.

6.8.1.10Вывести формулу периода малых колебаний математического

маятника.

6.8.1.11Как зависит период колебаний от начальных условий движения

маятника?

6.8.1.12Зависит ли период колебаний маятника от массы?

6.8.1.13Как изменяется частота колебаний маятника с уменьшением его

длины?

6.8.1.14Сколько раз за период потенциальная энергия маятника перехо-

дит в кинетическую?

6.8.1.15Что называется изохронностью колебаний?

6.8.2Физический маятник

6.8.2.1Дать определение физического маятника.

6.8.2.2Какая точка называется центром масс (центром инерции)

маятника?

6.8.2.3Какие внешние силы действуют на физический маятник?

6.8.2.4Записать дифференциальное уравнение качаний физического

маятника и привести его решение.

6.8.2.5Что называется приведенной длиной, центром и осью качаний

физического маятника?

6.8.2.6Каким свойством обладает ось подвеса и ось качаний физичес-

кого маятника?

6.8.2.7По какой формуле вычисляют период малых колебаний физичес-

кого маятника?

73

6.8.2.8Как зависит период от массы и момента инерции маятника и

почему?

6.8.2.9Дать определение оборотного маятника.

6.8.2.10Когда расстояние между опорными призмами равно приведенной длине маятника ℓпр? Свойство взаимности.

6.8.2.11Почему для определения ускорения свободного падения с помощью физического маятника используют маятник как оборотный?

6.8.2.12Как изменится ход маятниковых часов, если перенести их с экватора на полюс? Как нужно передвинуть груз маятника вдоль стержня,

если часы отстают?

6.8.2.13Что такое ускорение свободного падения? От чего оно зависит?

6.8.2.14Напишите рабочую формулу для определения ускорения g и поясните величины в нее входящие.

6.8.2.15Вывести формулы для вычисления относительной погрешнос-

ти измерения ускорения свободного падения εотн= g/g и абсолютной погрешности g.

Литература

1Савельев И.В. Курс общей физики. Т.1. – М.: Наука, 1986. – 432 с.

2Практикум по общей физике / Под ред. проф. В.Ф.Ноздрева. М.: Просвещение, 1971. – 311 с.

3Техническое описание прибора ФПIA. – Караганда. 1971.

4Физический практикум / Под ред. И.С. Ромченко. Ч.1. – М.: МИФИ, 1970. – 107 с.

5Погрешности измерений: методические указания, − Томск: ТПИ,

1984. – 23 с.

74

7 Определение моментов инерции твердых тел с помощью трифилярного подвеса

7.1 Цель работы

Целью работы является изучение вращательного движения и определение моментов инерции тел с помощью трифилярного подвеса.

7.2 Теоретическое введение

равен сумме моментов инерции составляющих его частей. Момент инерции

материальной точки равен произведению ее массы m на квадрат расстояния r до оси вращения:

Здесь dm и dV– масса и объём элемента тела, находящегося на расстоянии R от оси вращения, ρ – плотность тела в данной точке.

Одно и тоже тело относительно разных осей обладает различными

моментами инерции. В общем случае вычисление момента инерции тела

произвольной формы относительно той или иной оси вращения представляет собой довольно кропотливую в математическом отношении работу. Однако в некоторых случаях нахождение момента инерции значительно упрощяется,

75

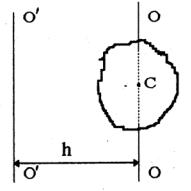
если воспользоваться теоремой Штейнера[1, 2]: момент инерции J относительно произвольной оси равен сумме момента инерции Jс относительно оси,

параллельной данной и проходящей через центр инерции тела, и произведения массы тела m на квадрат расстояния h между осями, как видно на рисунке 7.1:

В теореме Штейнера используется очень важное понятие: центр инерции тела. Центром инерции (или центром масс) тела называется точка С, положение которой задаётся радиусомвектором rс, определяемым следующим образом:

i=1

где mi – масса элемента с номером i, на которые мысленно разбивается тело, ri –радиус-вектор, определяющий положение i -ого элемента, N – число

N

элементов, m=∑ mi – масса тела.

i=1

О’О’– неподвижная ось вращения, ОО– проходящая через центр инерции тела, С− центр инерции тела

Рисунок 7.1 − Расположение осей в теореме Штейнера

Для выполнения данной работы нам понадобятся формулы, определя-

ющие моменты инерции цилиндра и параллелепипеда:

1) момент инерции однородного цилиндра (или диска) относительно оси, совпадающей с его геометрической осью:

76

где m – масса цилиндра, R – радиус цилиндра;

2) момент инерции однородного прямоугольного параллелепипеда относительно оси, проходящей через его центр инерции перпендикулярно

где m – масса параллелепипеда, а и b – длины сторон его основания. Выражения (7.7) и (7.8) были получены путём непосредственных

вычислений по формуле (7.4).

7.3 Описание метода измерений и установки

Используемый в данной работе метод определения момента инерции

основан на изучении крутильных колебаний тела, находящегося на трифи-

лярном подвесе [2] .Устройство трифилярного подвеса показано на рисун-

ке 7.2.

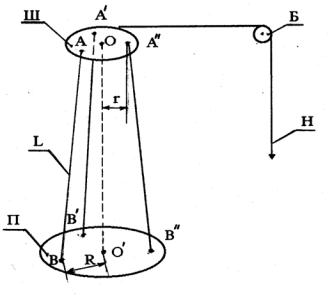
Ш– шайба, П– платформа, Б– блок, Н– нить, АВ=А’ В’=А” В” = l − три симметрично расположенные нити, R и r – расстояния от точек крепления нитей до центра платформы П и шайбы Ш соответственно.

Рисунок 7.2 − Схема трифилярного подвеса

Тело, момент инерции которого предстоит измерить, кладётся на

платформу П так, что центр инерции этого тела лежал на оси симметрии подвеса. Платформа П соединена с шайбой Ш тремя нитями АВ, А’В’ и А”В”. К шайбе Ш прикреплена нить Н, при помощи которой в системе можно возбудить крутильные колебания.

77

При повороте платформы на угол ϕ относительно положения равновесия её центр тяжести немного приподнимается. Возникает момент сил М, стремящийся вернуть платформу в положение равновесия. Величина момента сил пропорциональна углу поворота ϕ [2] :

где m – суммарная масса платформы и лежащих на ней тел. Подставляя

выражение (7.9) в формулу (7.1) основного закона вращательного движения, получим уравнение, описывающее движение платформы:

где J – суммарный момент инерции платформы и находящихся на ней тел относительно оси симметрии подвеса ОО. Уравнение (7.10) можно записать в виде

Уравнение (7.11) описывает гармонические колебания. Решение уравнения

имеет вид

где ϕ0 − амплитуда колебаний, α − начальная фаза, ω − циклическая частота колебаний. Период колебаний T связан с циклической частотой соотношением

Таким образом, выведенная из положения равновесия платформа трифилярного подвеса будет совершать гармонические колебания. Период колебаний можно найти, подставив выражение (7.12) в формулу (7.14):

Формула (7.15) лежит в основе метода измерения момента инерции с помощью трифилярного подвеса. Возведя левую и правую части формулы (7.15) в квадрат и выполнив простые преобразования, получим рабочую формулу для определения момента инерции:

78

Формула (7.16) позволяет вычислить момент инерции платформы с телом по периоду колебаний, если известны геометрия прибора (величины R, r, l) и масса платформы с телом.

Чтобы найти момент инерции какого-либо тела, нужно сначала из наблюдений за колебаниями ненагруженной платформы П найти по формуле (7.16) её момент инерции Jпл относительно оси установки. Затем, расположив испытуемое тело на платформе таким образом, чтобы центр тяжести тела лежал на оси подвеса, определить период колебаний прибора и найти суммарный момент инерции JΣ платформы вместе с телом. Поскольку

момент инерции – аддитивная величина, вычтя из JΣ момент инерции ненагруженной платформы, можно найти искомый момент инерции Jc :

Таким способом находят момент инерции тела относительно оси, проходящей через его центр инерции. Зная эту величину, можно по теореме Штейнера найти момент инерции тела относительно оси, параллельной данной. Помещая два одинаковых тела на платформу симметрично отно-

1)моменты инерции тел, имеющих форму цилиндра и прямоугольного параллелепипеда, относительно оси, проходящей через центр инерции;

2)моменты инерции прямоугольного параллелепипеда относительно оси, которая не проходит через центр инерции.

Затем сравнить экспериментально полученные значения моментов инерции тела с теоретически вычисленными.

7.4 Безопасность труда

В работе используются тела, имеющие массу до 1 кг. Необходимо соблюдать осторожность в моменты установки тел на платформу и снятия их с платформы, чтобы избежать случайного падения тел.

7.5 Порядок выполнения работы

Приборы и принадлежности: трифилярный подвес, набор тел, секундомер, штангенциркуль.

7.5.1 Определить период колебания ненагруженной платформы и вычислить её момент инерции Jпл по формуле (7.16), результаты занести в таблицу 7.1. Период колебаний системы Т определяется путём измерения времени t секундомером N= (30 - 50) колебаний по формуле:

Т=t / N .

79

Каждое определение периода нужно производить не менее 3-х раз. В качестве периода принимается среднее арифметическое значение. Амплитуда колебаний должна быть не более 6 - 8 О .

Таблица 7.1 − Момент инерции платформы

1

2

3

7.5.2 Поместить цилиндр на платформу так, чтобы его центр инерции лежал на оси вращения подвеса. Измерить период колебания нагруженной

платформы и определить по формуле (7.16) суммарный момент инерции JΣ

платформы вместе с телом. Момент инерции цилиндра Jцил рассчитать по формуле:

Jцил = JΣ - Jпл .

Результаты занести в таблицу 7.2.

7.5.3Определить моменты инерции J1п и J2п параллелепипедов 1 и 2 соответственно. Измерения провести аналогично п.7.5.2. Результаты занести

втаблицы 7.3, 7.4, 7.5.

7.5.4Поместить оба параллелепипеда на платформу, положив их друг на друга так, чтобы центр тяжести каждого из них лежал на оси вращения подвеса. Найти их общий момент инерции J1,2п .

Таблица 7.2 − Момент инерции цилиндра

80