Лабораторные по физике

ходима для того, чтобы началось разрушение; окончательное же разрушение происходит при нагрузке, изображаемой на диаграмме ординатой FК точки К.

Напряжение, вызванное наибольшей нагрузкой, носит название предела прочности или временного сопротивления σВ .

При напряжении, превышающем предел прочности, в одном из сечений стержня образуется сужение, называемое шейкой. В дальнейшем деформация сосредоточивается в этом сечении и возрастает даже при уменьшении растягивающей силы. Это и приводит к разрушению материала (точка К диаграммы).

Механические характеристики (пределы пропорциональности, упругости, текучести и прочности) характеризуют способность материала сопротивляться стремлению внешних сил деформировать и разрушать образец при растяжении. Если, например, предел прочности близок к пределу упругости, то такое тело дает лишь незначительные остаточные деформации: оно называется хрупким (например, закаленная сталь). Тела, способные давать большие пластические деформации, называются пластичными; так, например, свинцовые или цинковые проволоки обнаруживают значительные пластические деформации.

В настоящей работе требуется определить модуль Юнга по упругой

деформации растяжения проволоки длиной l. Нагрузка создается с помощью i грузов суммарным весом Рi (здесь и ниже общее обозначение силы F для случая веса заменено на обозначение Р), для определения абсолютной деформации l используется катетометр.

5.3 Описание катетометра

Катетометр КМ-6 предназначен для измерения расстояний между двумя точками на одной вертикали на недоступных для непосредственного измерения объектах, расположенных на расстояниях нескольких десятков сантиметров от объектива зрительной трубы катетометра [2,3].

Катетометр, показанный на рисунке 5.5, состоит из вертикального штатива с колонкой 1 на треножнике, измерительной каретки 2, зрительной трубы 3 и отсчетного микроскопа 4. В колонку вмонтирована стеклянная миллиметровая шкала, ось которой строго параллельна оси колонки. Подъемными винтами 5 треножника колонку можно устанавливать по круглому уровню 15 строго вертикально. С помощью ручек 6 колонку можно поворачивать вокруг вертикальной оси. Для точной наводки поворот колонки осуществляется микрометрическим винтом 7 при закрепленном винте 8.

Измерительная каретка 2, несущая зрительную трубу 3 и отсчетный микроскоп 4, перемещается по колонке на роликах. Грубое перемещение каретки по вертикали осуществляется от руки при открепленном винте 9, точное – с помощью микрометрического винта 10 при закрепленном винте 9.

51

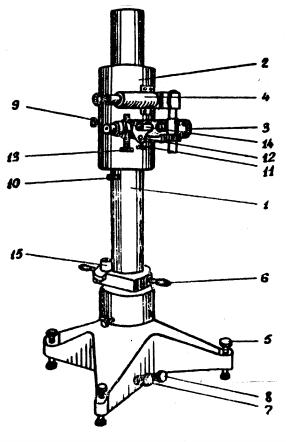
Зрительная труба 3 укреплена на каретке. Фокусировка трубы на выбранную точку объекта производится вращением маховичка 11, грубая наводка осуществляется с помощью механического визира, состоящего из целика и мушки, укрепленных на тубусе зрительной трубы. Сбоку на тубусе имеется цилиндрический уровень 12, ось которого параллельна визирной оси трубы. Уровень устанавливается в горизонтальное положение микрометрическим винтом 13 путем совмещения рассматриваемого через лупу 14. При совмещенных половинках пузырька визирная ось зрительной трубы принимает строго горизонтальное положение.

Точная наводка зрительной трубы в горизонтальной плоскости производится поворотом колонки микрометрическим винтом 7 при закрепленном винте 8.

Рисунок 5.5 – Катетометр

Измерительная система катетометра состоит из зрительной трубы и отсчетного микроскопа с осветительной системой. В фокальной плоскости окуляра отсчетного микроскопа установлена масштабная сетка, на которую специальным оптическим устройством проецируется миллиметровая шкала,

52

как показано на рисунке 5.7. Масштабная сетка разделена в вертикальном и горизонтальном направлениях на десять частей. Отсчетный микроскоп установлен таким образом, что десять горизонтальных биссекторов сетки укладываются между двумя штрихами миллиметровой шкалы, следовательно, каждому биссектору в вертикальном направлении соответствует одна десятая доля миллиметра. В горизонтальном направлении десятая часть биссектора равна одной сотой миллиметра. Тысячные доли миллиметра оцениваются на глаз в долях делений. Измерение расстояний между двумя точками производится с помощью зрительной трубы и отсчетного микроскопа путем сравнения измеряемой длины с миллиметровой шкалой. А именно, перемещая каретку со зрительной трубой и отсчетным микроскопом по колонке вдоль миллиметровой шкалы, а также вращая колонку вокруг вертикальной оси, устанавливают трубу на выбранные точки объекта; отсчеты снимают через окуляр отсчетного микроскопа по шкале и масштабной сетке. Длины вертикальных отрезков определяют как разность соответствующих отсчетов по шкале.

Катетометр снабжен набором сменных насадочных линз. На объектив зрительной трубы надевается та или иная линза в зависимости от расстояния от объекта до измеряемого предмета. Расстояния указаны на оправах линз. Катетометр снабжен также трансформатором для включения в сеть осветительной части отсчетного микроскопа.

5.4 Методика измерений

5.4.1Перед измерением с помощью подъемных винтов треножника 5 по круглому уровню 15 (см.рисунок 5.5) ось колонки устанавливается в строго вертикальном положении.

5.4.2Осветительная часть отсчетного микроскопа включается через трансформатор в сеть.

5.4.3Винт 9 открепляется, измерительная каретка поднимается на уровень выбранной точки объекта. С помощью целика и мушки труба грубо устанавливается на выбранную точку.

5.4.4Окуляр зрительной трубы путем вращения устанавливается на резкое изображение сетки; фокусировка трубы на резкое изображение объекта производится вращением маховика 11. После этого производится точная наводка трубы на выбранную точку объекта: в вертикальной плоскости с помощью винта 10 при закрепленном винте 9, в горизонтальной плоскости – с помощью винта 7 при закрепленном винте 8.

5.4.5Сетка зрительной трубы имеет перекрестие, показанное на рисунке 5.6, правый горизонтальный штрих которого выполнен в виде углового биссектора. При наводке трубы выбранная точка объекта должна располагаться в правой половине углового биссектора на уровне горизонтального

53

штриха. При этом необходимо следить за цилиндрическим уровнем 12, изображения половинок пузырька которого должны образовывать дугу.

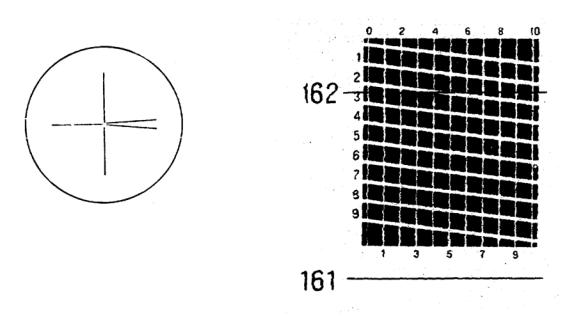
5.4.6 После этого снимается первый отсчет по масштабной сетке. Производство отсчета легко уяснить из следующего примера. В поле зрения отсчетного микроскопа одновременно видны изображения двух штрихов миллиметровой шкалы, обозначенные крупными цифрами, и масштабная сетка, как показано на рисунке 5.7. Индексом для отсчета целых миллиметров служит нулевой биссектор десятых долей миллиметра, расположенный вверху масштабной сетки.

На рисунке 5.7 штрих "162" прошел нулевой биссектор, а ближайший большой штрих еще не дошел до нулевого биссектора. Отсчет будет 162 мм плюс отрезок от штриха "162" до нулевого биссектора. В этом отрезке число десятых долей миллиметра будет обозначено цифрой последнего пройденого биссектора, в данном случае цифрой "2". Отсчет сотых и тысячных долей миллиметра производится в горизонтальном направлении сетки, там, где миллиметровый штрих шкалы пересекает наклонную светлую полоску сетки, точнее по точке пересечения штриха и продольной оси симметрии светлой

полоски. На рисунке эта точка находится между пятым и шестым делениями сетки, что соответствует 0,255 мм. Тысячные доли миллиметра отсчитываются на глаз по положению точки между вертикальными делениями сетки. Окончательный отсчет будет 162,255 мм.

5.4.7 Перемещением каретки по колонке, наводится зрительная труба на вторую точку измеряемого объекта и, проверив установку по цилиндрическо-

54

му уровню, снимается второй отсчет. Разность между двумя отсчетами даст измеренную величину отрезка.

Следует отметить, что в процессе измерений данного отрезка изменение перефокусировки на объект не допускается, так как это вносит погрешность в измерения.

5.5 Безопасность труда

В работе используется катетометр, на осветительную лампу которого подается напряжение 3,5 В, снимаемое с трансформатора 220/3,5. Корпус трансформатора изготовлен из изоляционного материала, что исключает возникновение на нем опасного напряжения.

В работе используются грузы весом по 0,2 кг каждый, общий вес грузов около 1 кг. Необходимо соблюдать осторожность при навешивании грузов, чтобы избежать их падения.

5.6 Порядок выполнения работы

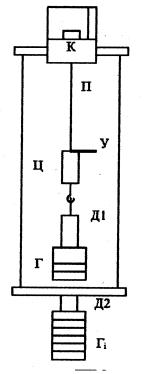
Исследуемая проволока П своим верхним концом прочно укреплена в зажиме кронштейна К, как показано на рисунке 5.8, на нижнем конце укреплен цилиндр Ц, основание которого снабжено крючком для подвеса держателя Д1. Проволока натянута (выпрямлена) при помощи груза Г, установленного на держателе Д1.

Рисунок 5.8 – Схема установки

55

8) по формуле (5.5) для каждого значения нагрузки вычислить модуль Юнга Еi ;

9)найти среднее арифметическое значение Еср;

10)результаты измерений и вычислений занести в таблицу 5.1.

11)записать в таблицу 5.2 абсолютные погрешности непосредственно

измеряемых величин l, n, mi, d.;

12) по результатам эксперимента построить график зависимости напря-

5.7 Оценка погрешности результата измерений

5.7.1 Подсчитать относительную и абсолютную погрешности измере-

Расчет выполнить, как для косвенных измерений [4].

5.7.2 Перейти в равенстве (5.6) к непосредственно измеряемым в опыте величинам, используя зависимости li = ni – n0 , Pi = mi g и S = π d2/4.

5.7.3Применяя к полученному выражению для Еi операции

логарифмирования и дифференцирования по параметрам l, ni, n0, mi, d, получить соотношение для вычисления относительной погрешности

5.7.5По данным таблиц 5.1 и 5.2 найти численное значение отно-

сительной погрешности εотн = Еi / Еi , используя измерения одного i-го опыта.

5.7.6Вычислить абсолютную погрешность

Еi = εотн Еi ,

где Еi – значение модуля Юнга в i-ом опыте.

57

5.7.7 Написать вывод. Сравнить полученное значение Еср с табличными значениями модулей Юнга (модулей упругости) различных материалов. Определить по модулю Юнга материал исследуемой проволоки. Результат опыта представить в виде:

Е=(Еср ± Е) Н/м2.

5.8 Контрольные вопросы

5.8.1Что называется деформацией?

5.8.2Как связан характер деформаций со структурой, строением

материала?

5.8.3Чем отличаются кристаллические тела от аморфных? Приведите примеры поликристаллических и аморфных тел.

5.8.4За счет чего происходит деформация тел?

5.8.5Какие деформации называются упругими и какие пластическими? Остаточные деформации. Чем отличаются упругие деформации от пластических?

5.8.6Перечислите основные виды деформаций твердых тел в зависимости от действующих на них сил.

5.8.7Как возникают внутренние упругие силы в теле?

5.8.8В чем состоит метод сечений?

5.8.9Что называется механическим напряжением и в каких единицах оно измеряется в системе СИ? Какие напряжения называются нормальными?

5.8.10.Какова цель испытания материалов на растяжение?

5.8.11Сформулировать закон Гука и указать границы его применимости.

5.8.12Что называется абсолютной деформацией? Относительной деформацией?

5.8.13Какой физический смысл имеет модуль Юнга. В каких единицах он измеряется в системе СИ?

5.8.14Построить диаграмму растяжения и пояснить на ней ход зависи-

мости между внешней силой F и величиной вызванной ею деформации l.

5.8.15Перечислить важнейшие характеристики прочности материала и дать их определения.

5.8.16Назвать характеристики пластичности материала. Какая из них лучше характеризует пластические свойства и почему?

5.8.17Какая механическая характеристика материала связана с углом наклона прямолинейного участка диаграммы растяжения?

5.8.18Какие материалы называются хрупкими?

5.8.19Объяснить, как настроить зрительную трубу катетометра на исследуемый объект.

58

5.8.20Объяснить, как снять отсчет по отсчетному микроскопу катето-

метра.

5.8.21Объяснить, какие величины заносятся в таблицу измерений.

5.8.22Вывести формулу для расчета относительной погрешности измерения модуля упругости Е, как для косвенных измерений.

Литература

1Савельев И.В. Курс общей физики. Т.1.-М.: Наука, 1982. – 432 с.

2Катетометр КМ-6. Инструкция к пользованию. – Ленинград:

ЛООМД, 1964. – 16 с.

3Физический практикум / Под редакцией И.С.Ромченко. Ч.1. – М.:

МИФИ, 1970. – 107 с.

4Погрешности измерений: методические указания. – Томск: ТПИ, 1984. – 23 с.

59

6 Изучение математического маятника и определение ускорения свободного падения с помощью оборотного маятника

6.1 Цель работы

Целью данной работы является: изучение математического маятника (исследование зависимости периода колебаний математического маятника от его длины и массы) и определение ускорения свободного падения с помощью оборотного маятника.

6.2 Теоретическое введение

6.2.1 Математический маятник

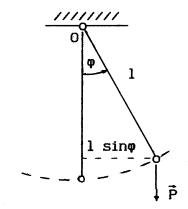
Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке. Достаточно хорошим приближением к математическому маятнику является устройство, представляющее собой небольшой тяжелый шарик, подвешенный на длинной тонкой нити, показанный на рисунке 6.1 [1].

Рисунок 6.1− Математический маятник

Отклонение маятника от положения равновесия будем характеризовать углом ϕ, образованным нитью с вертикалью. На маятник действуют внешние силы: сила тяжести Р и реакция оси подвеса О. При отклонении маятника от положения равновесия возникает момент силы Р относительно оси О, стремящийся вернуть маятник в положение равновесия. Если сила лежит в плоскости, перпендикулярной данной оси, то ее момент относительно этой оси равен по величине произведению силы на плечо (расстояние от оси до прямой, вдоль которой действует сила). При повороте маятника на угол ϕ в одном направлении сила Р стремится вращать его в противоположном направлении. Следовательно, знак момента силы Р относительно оси О противоположен знаку угла поворота маятника ϕ и sin ϕ.

60