Лабораторные по физике

Результаты измерения диаметра капилляра заносятся в таблицу 4.2, остальных измерений – в таблицу 4.3.

4.5.1Измерить при помощи микроскопа диаметр капилляра. Для этого срез капилляра поместить на предметное стекло микроскопа. Совместить визирные линии окуляр-микрометра с правым, а затем с левым краями отверстия капилляра, как на рисунке 4.4. Снять отсчеты по горизонтальной шкале (целые миллиметры) и по шкале барабана (десятые и сотые доли миллиметра). Найти диаметр капилляра как разность этих отсчетов. Диаметр капилляра измерить в трех различных направлениях. За диаметр капилляра принять среднее арифметическое полученных результатов. Вычислить радиус R капилляра.

4.5.2С помощью весов определить массу m1 пустого стакана 4 с точностью до 0,01 г.

4.5.3Измерить линейкой начальную высоту уровня жидкости h' от плоскости стола.

1 – горизонтальная шкала; 2 – шкала барабана; 3 – поле зрения микроскопа Рисунок 4.4 – Схема измерения диаметра капилляра

4.5.4Быстро опустить капилляр из положения А в положение В (см. рисунок 4.3), так чтобы жидкость стекала в стакан 4 и включить секундомер.

4.5.5Измерить высоту h конца капилляра от плоскости стола.

4.5.6Когда жидкости в стакане 4 будет достаточно (1/2 объёма), выключить секундомер, быстро подняв при этом капилляр в положение А. Считать с секундомера время истечения жидкости t.

4.5.7Измерить конечный уровень жидкости h'' в сосуде 1.

4.5.8Определить массу m2 стакана с жидкостью.

4.5.9 Занести в таблицу 4.3 значения: ускорение силы тяжести

(g = 9,8 м/с2), плотности жидкости (ρводы = 103кг/м3) и длину капилляра, значение которой указано на установке.

41

4.5.10Вычислить значения массы жидкости m, средней высоты столба Н

изанести в таблицу 4.3.

4.5.11Рассчитать по рабочей формуле (4.14) значение коэффициента

динамической вязкости η.

4.5.12 По таблице 4.1 построить график зависимости вязкости воды от температуры. По найденному значению вязкости и графику оценить температуру воды.

Таблица 4.2 – Результаты измерений диаметра капилляра

Таблица 4.3 – Результаты измерений и вычислений

4.6 Оценка погрешности измерений

Абсолютная и относительная погрешности измерений коэффициента динамической вязкости находится грубым методом расчёта погрешностей [4] исходя из рабочей формулы (4.14).

42

4.6.1Определить и обосновать значения абсолютных погрешностей непосредственно измеряемых величин, входящих в формулу (4.14) (H, R, t, L, m).

4.6.2Получить формулу для вычисления относительной погрешности

ε= Δη / η, исходя из рабочей формулы (4.14), логарифмируя и дифференцируя её по величинам H, R, t, L ,m.

4.6.3Вычислить относительную погрешность измерения коэффициента вязкости ε = Δη / η.

4.6.4Вычислить абсолютную погрешность Δη = ε ·η.

4.6.5Написать вывод. Значение η привести в форме (η + Δη), Па с.

4.7 Контрольные вопросы

4.7.1Дать определение турбулентного и ламинарного течений.

4.7.2Что такое вязкость?

4.7.3Сформулировать основной закон внутреннего трения.

4.7.4Какой механизм внутреннего трения в газах?

4.7.5Какой механизм внутреннего трения в жидкостях?

4.7.6Как распределены скорости при ламинарном течении жидкости в

трубе?

4.7.7Какие силы действуют на жидкость при ламинарном движении в

трубе?

4.7.8Что такое расход жидкости.

4.7.9Выведите формулу Пуазейля.

4.7.10Получите из формулы Пуазейля рабочую формулу (4.14) для нахождения коэффициента внутреннего трения.

Литература

1Савельев И.В. Курс общей физики. Т.1. – М.: Наука, 1982. – 432 с.

2Сивухин Д.В. Общий курс физики. Т.1. – М.: Наука, 1979. – 520 с.

3Руководство к лабораторным занятиям по физике / Под ред. Л.Л.Гольдина. – М.: Наука, 1973. – 688 с.

4Погрешности измерений: методические указания. – Томск: ТПИ, 1984,

–23 с.

43

5 Определение модуля Юнга по деформации растяжения

5.1 Цель работы

Цель работы – изучение поведения деформируемых тел при действии на них внешних сил и экспериментальное определение модуля Юнга по деформации растяжения.

5.2 Теоретическое введение

Втеоретической механике (статике) изучается равновесие абсолютно твердого тела; этого представления о материале достаточно для решения поставленной в статике задачи – определения условий, при которых возможно взаимное уравновешивание приложенных к телу сил. При изучении сопротивления материалов действию этих сил такого грубого приближенного представления о свойствах материала уже недостаточно; мы должны учесть, что абсолютно твердых тел в природе не существует.

Вдействительности тела под действием приложенных к ним сил в той или иной степени меняют свою форму и размеры, то есть деформируются. Величины и характер деформаций связаны со структурой, строением применяемых нами материалов. Все эти материалы могут быть разбиты на два класса: кристаллические и аморфные [1].

Кристаллические материалы состоят из громадного количества хаотически расположенных относительно друг друга мелких кристалликов. Известно, что в отдельном кристалле (монокристалле) атомы располагаются в определенном порядке, образуя кристаллическую решетку. Кристаллическую структуру имеют металлы (поликристаллические тела). В аморфных телах (стекло, смолы и т.п.) в отличие от кристаллов нет строгого порядка в расположении атомов. Только ближайшие атомы-соседи располагаются в некотором порядке. Но строгой повторяемости во всех направлениях одного

итого же элемента структуры, которая характерна для кристаллов, в аморфных телах нет.

Атомы удерживаются в равновесии силами взаимодействия. Деформация тел происходит за счет изменения расположения атомов, их сближения или удаления. Деформации разделяются на упругие и пластические. Упругими деформациями называются такие изменения формы и размеров элементов, которые исчезают после удаления вызвавших их сил, – тело полностью восстанавливает свою прежнюю форму. Эти деформации связаны лишь с упругими искажениями решетки атомов. Опыт показывает, что упругие деформации наблюдаются, пока величина внешних сил не превзошла известного предела.

Если же внешние силы перешли этот предел, то в результате смещения атомы и молекулы меняют своих "соседей" и начинают взаимодействовать с

44

другими. После прекращения действия внешних сил они уже не возвращаются к прежнему положению, форма и размеры элемента не восстанавливаются в первоначальном виде. Такие деформации называются пластическими. Пластические деформации сохраняются в теле после снятия нагрузки, поэтому их еще называют остаточными. В кристаллических материалах эти деформации связаны с необратимыми перемещениями одних слоев кристаллической решетки относительно других.

В зависимости от направления действия сил, приложенных к телу, могут возникать различные виды деформаций: растяжение, сжатие, сдвиг, кручение, изгиб. Мы будем знакомиться с деформацией тел наиболее простой формы. К таким телам относятся так называемые призматические стержни с прямой осью. Кроме того, будем считать, что сам стержень не имеет массы.

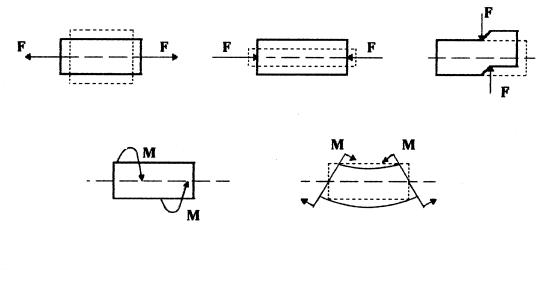
а –растяжение; б –сжатие; в –сдвиг; г –кручение; д –изгиб Рисунок 5.1 – Виды деформаций

Деформация растяжения или сжатия возникает в том случае, когда внешние силы направлены по одной прямой (вдоль оси стержня) в разные стороны, как на рисунке 5.1,а,б. Если на стержень действуют внешние силы, стремящиеся сдвинуть одну часть его относительно другой, то возникает деформация сдвига. При этом, как видно из рисунка 5.1,в, силы образуют пару с небольшим плечом в плоскости продольной оси стержня. Если стержень находится под действием нагрузок, создающих противоположные пары сил в плоскостях, перпендикулярных продольной оси стержня, то появляется деформация кручения, показанная на рисунке 5.1,г. И, наконец, если две пары сил разного знака действуют в плоскости продольной оси стержня, то создается деформация изгиба, показанная на рисунке 5.1,д.

45

В теории упругости доказывается, что все типы деформаций могут быть сведены (при условии, что они достаточно малы) к одновременно происходящим деформациям растяжения (или сжатия) и сдвига.

Смещение атомов при деформации материала под действием внешних сил сопровождается изменением сил взаимодействия между атомами – сил притяжения и отталкивания. Во всяком твердом теле под действием внешних сил возникают дополнительные внутренние силы, сопровождающие де-

формацию материала. Эти внутренние силы сопротивляются стремлению внешних сил разрушить тело, изменить его форму, отделить одну его часть от другой. Они стремятся восстановить прежнюю форму и размеры деформированной части тела. Отсюда следует, что для решения задач сопротивления материалов необходимо прежде всего научиться по внешним силам определять внутренние силы упругости. Для этого применяют метод сечений, сущность которого заключается в следующем.

Пусть к концу однородного стержня с площадью поперечного сечения S приложена сила F, действующая на все сечение стержня равномерно, другой конец стержня закреплен, как показано на рисунке 5.2,а.

Разделим мысленно стержень на две части сечением m-n, перпендикулярным его оси, как на рисунке 5.2,б, и определим силы, с которыми эти части стержня действуют друг на друга. Так как обе части стержня находятся в равновесии, то векторная сумма сил, действующих на каждую из них, должна быть равна нулю. Отбросим верхнюю часть и рассмотрим равновесие нижней (см. рисунок 5.2,в,г). Равновесие этой части не нарушится лишь в том случае, если к ней приложить реакции – внутренние силы, заменяющие

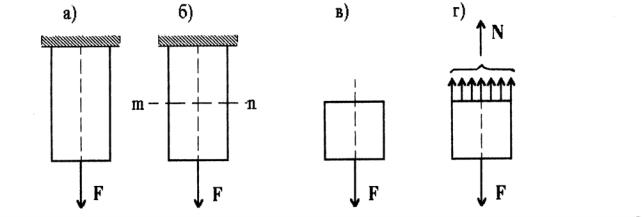
а – исходная схема нагружения стержня; б –стержень рассекается плоскостью; в – отсеченная часть стержня; г – равновесие отсеченной части стержня

Рисунок 5.2 – Метод сечений

действие отброшенной части. Внутренние силы будут уравновешивать внешнюю силу F, поэтому они должны сложиться в равнодействующую N, рав-

46

ную по модулю F и направленную по оси стержня в сторону, противоположную внешней силе, то есть N = -2F. Такая же по величине, но направленная вниз сила действует по третьему закону Ньютона со стороны нижней части на верхнюю. Равнодействующая N внутренних сил называется усилием, передающимся через сечение S от одной части стержня на другую и обратно. В этом и состоит метод сечений.

Величина внутренних сил упругости, приходящаяся на единицу площади поперечного сечения тела, называется механическим напряжением и обозначается буквой σ. Напряжение, следовательно, является мерой внутренних сил, возникающих в теле при деформации. Для однородного, растянутого, нагруженного по концам стержня напряжения остаются постоянными как по сечению, так и по длине, то есть сохраняются во всех точках объема, занимаемого телом. Такое напряженное состояние называется однородным. При однородном напряженном состоянии все точки тела находятся в одинаковых условиях и

то есть напряжение численно равно отношению внешней силы F к площади поперечного сечения стержня S. Единица измерения напряжения Н/м2, 1Н/м2 называется паскаль (Па).

В рассматриваемом примере направление силы нормально к выбранной нами площадке, и возникающее в этом случае напряжение на площадке S

является нормальным напряжением.

Для того, чтобы иметь полную картину работы растянутого или сжатого стержня, необходимо установить зависимость между его деформацией и величиной деформирующей силы. Соответствующие законы можно получить лишь на основании опытов с растяжением и сжатием образцов изучаемого материала; эти же опыты дают возможность изучать и прочность материала, определять его предел прочности и другие характеристики. Для осуществления подобных опытов в лабораториях пользуются специальными устройствами, позволяющими деформировать образцы и доводить их до разрушения, измеряя требуемую для этого величину усилий. Одновременно при помощи достаточно точных измерительных приборов (в данной работе используется катетометр) производят измерения деформаций образцов.

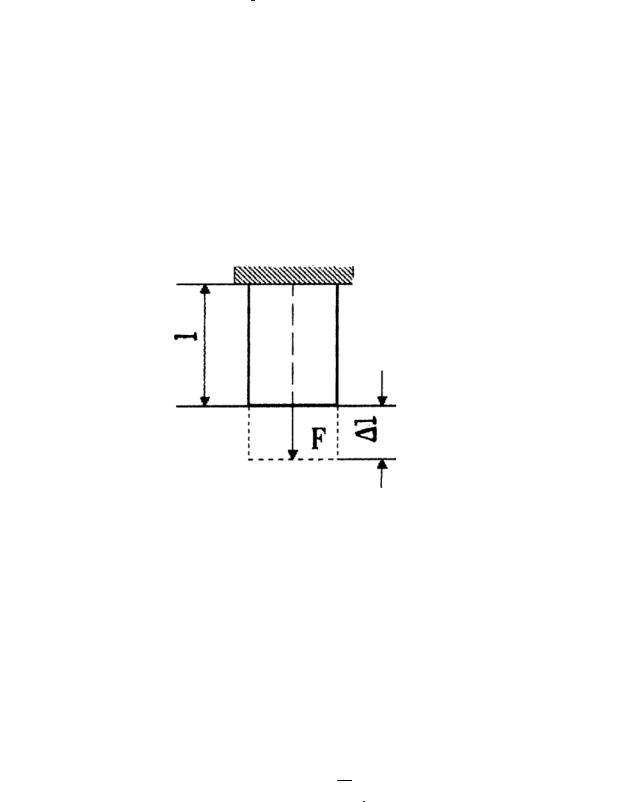
Опыты приводят к заключению, что пока нагрузка на образец не достигла известного предела, удлинение прямо пропорционально растягивающей силе F, длине образца l и обратно пропорционально площади поперечного

сечения S, как на рисунке 5.3.Обозначая через l приращение длины образца от силы F, можно написать формулу, связывающую между собой эти опытные данные:

47

откуда следует: модуль Юнга Е равен напряжению, возникающему при относительной деформации, равной единице. Чем больше величина Е, тем менее растягивается (сжимается) стержень при прочих равных условиях (длине, площади, силе F). Таким образом, физически модуль Е характеризует сопротивляемость материала упругой деформации при растяжении (сжатии).

Так как l/l – относительное удлинение – является безразмерной величиной, то из формулы (5.5) следует, что модуль выражается в тех же единицах, что и напряжение σ, то есть в Н/м2. Для наиболее часто применяемых материалов модуль упругости Е в Н/м2 имеет следующие значения:

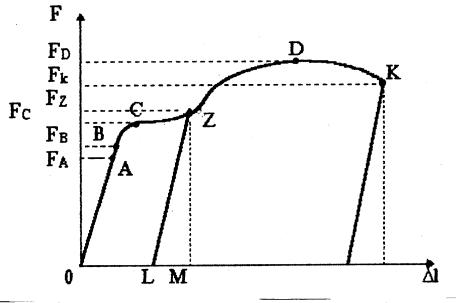
Всякое твердое тело дает деформации, подчиняющиеся закону Гука лишь до известного предела. Рассмотрим поведение материалов в опыте на растяжение вплоть до разрушения. Результаты измерений нагляднее всего можно представить в виде так называемой диаграммы растяжения. При вычерчивании диаграммы по вертикальной оси откладываются в определенном масштабе нагрузки, а по горизонтальной – абсолютные удлинения. При растяжении образца из пластичного материала (например, малоуглеродистой стали) диаграмма имеет вид, показанный на рисунке 5.4.

Прямолинейный участок ОА соответствует упругим деформациям образца. Ордината FА представляет собой величину растягивающей силы, соответствующей пределу пропорциональности σП , то есть тому наибольшему напряжению, превышение которого вызывает отклонение от закона Гука.

При увеличении растягивающей силы за величину FА деформация начинает расти быстрее нагрузки – диаграмма имеет криволинейный вид с выпуклостью вверх. Однако до точки В деформации упругие, то есть образец восстанавливает свою форму после снятия нагрузки. За точкой В появляются неупругие деформации.

Напряжение, при превышении которого в теле появляются остаточные деформации, называется пределом упругости σу; на диаграмме нагрузка, вызывающая это напряжение, измеряется ординатой FВ.

49

Точки А и В настолько близки друг другу, что обычно считают предел упругости и предел пропорциональности совпадающими. Поэтому зачастую говорят, что материал следует закону Гука, пока не достигнет предела упругости, хотя правильнее было бы сказать – предела пропорциональности.

Рисунок 5.4 –Диаграмма растяжения малоуглеродистой стали

При некотором значении растягивающей силы Fс материал "течет"; для увеличения деформации почти не нужно увеличивать растягивающую силу. На диаграмме образуется горизонтальная (или почти горизонтальная) площадка.

Напряжение, при котором происходит такое течение материала – рост деформаций при постоянной (примерно) нагрузке, называется пределом текучести σт.

После образования площадки текучести материал вновь начинает сопротивляться дальнейшему растяжению, и для увеличения удлинения l приходится увеличивать силу. Точка D диаграммы соответствует наибольшей величине нагрузки.

Если снять нагрузку в состоянии, описываемом некоторой точкой Z, лежащей между точками С и D, то при разгрузке диаграмма будет изображаться прямой ZL, примерно параллельной прямой ОА. Таким образом, образец в этом случае не вернется к первоначальным размерам; отрезок LM будет представлять упругое удлинение, по-прежнему меняющееся пропорционально нагрузке с прежним модулем упругости; отрезок OL – остаточное удлинение и отрезок ОМ полное удлинение при нагрузке Fz.

Наибольшая величина растягивающей стержень силы изображается ординатой FD; она часто называется разрушающей нагрузкой, так как необ-

50