
- •ОПТИКА. АТОМНАЯ ФИЗИКА
- •Содержание
- •1 Определение показателя преломления жидкостей и концентрации сахара в растворе при помощи рефрактометра
- •3 Исследование явления интерференции световых волн с помощью интерферометра Рэлея
- •6 Исследование дисперсии стеклянной призмы
- •7 Изучение внешнего фотоэффекта
- •8 Определение постоянной Стефана-Больцмана и постоянной Планка
- •9 Изучение серии Бальмера и определение постоянной Ридберга
- •12 Законы поляризации света
3 Исследование явления интерференции световых волн с помощью интерферометра Рэлея
3.1 Цель работы
Изучение явления интерференции света, устройства и принципа работы интерферометра Рэлея. Определение показателя преломления и неизвестной концентрации растворенного вещества с помощью интерферометра Рэлея.
3.2Теоретическая часть
3.2.1Интерференция колебаний. Когерентность
Рассмотрим сложение двух гармонических колебаний с одинаковой частотой ω, происходящих в одном направлении:
a1 = a01 sin(ωt +α1 ),
a2 = a02 sin(ωt +α2 ) ,
где a01 и a02 – амплитуды колебаний; α1 и α2 – начальные фазы
колебаний; t – время. В результате сложения этих колебаний вновь образуется гармоническое колебание:
a = a0 sin(ωt +ϕ),
где амплитуда a0 и разность фаз ϕ определяются выражениями:
a02 = a012 + a022 + 2a01a02 cos(α1 −α2 ),
tgϕ = a01 sin((α1 ))+ a02 sin((α2 )). a01 cos α1 + a02 cos α2
Результат сложения колебаний зависит от разности фаз δ =α2 −α1 исходных колебаний. Амплитуда результирующего колебания a0 может
принимать любое значение в интервале от (a01 −a02 )2 при δ =π до
(a01 + a02 )2 при δ = 0 .
Энергетической характеристикой колебаний является физическая величина – интенсивность I , значение которой пропорционально квад-
рату амплитуды (I a02 ). Вычислим среднее значение квадрата амплитуды за промежуток времени τ :
|
τ |
τ |
|
|
a02 |
= τ1 ∫a02dt = a012 + a022 |
+ 2a01a02 τ1 ∫cos(δ )dt . |
(3.1) |
|
|
0 |
0 |
|
|
Если разность фаз δ |
имеет случайный характер и за промежуток времени |
|||
τ она многократно |
принимает значения в интервале |
от |
0 до 2π , то |
|
τ |
|
|
|
|
интеграл ∫cos(δ )dt |
стремится к нулю. |
В этом случае |
a02 |
определяется |
0 |
|
|
|
|
выражением: |
a02 = a012 |
+ a022 . |
|
|
23

Соответственно интенсивность I |
результирующих колебаний равна сумме |
||||||||
интенсивностей I1 |
и I2 исходных колебаний: |
|
|
|
|||||
|
|
|
|
I = I1 + I2 . |
|
|
|
||
Если разность фаз δ не зависит от времени, то выражение (3.1) принимает |
|||||||||
вид: |
|
|
|
|
|
|
cos(δ ). |
||
|
|
a2 |
= a2 |
+ a2 + 2a |
a |
02 |
|||
|
|
0 |
01 |
02 |
01 |
|
|
||
В этом случае интенсивность I результирующих колебаний в зависимости |
|||||||||
от разности фаз δ может быть больше или меньше суммы интенсивностей |
|||||||||
исходных колебаний: |
|
|
|
|
|
|
|||
|
|
I = I1 + I2 + 2 I1 I2 cos(δ ). |
(3.2) |
||||||
Колебания, при сложении которых I ≠ I1 + I2 , |
называются когерентными. |
||||||||
Явление усиления или ослабления интенсивности колебания в результате |
|||||||||
сложения когерентных колебаний называется интерференцией |
|||||||||
колебаний. |
|
|
|
|
|
|
|
||
3.2.2 Интерференция световых волн. Условия максимума и |
|||||||||
минимума |
|
|
|
|
|
|
|
||
По аналогии с определениями в 3.2.1 принято говорить об интер- |
|||||||||
ференции волн, если при их сложении не имеет места суммирование |
|||||||||
интенсивностей. Очевидно, что возможна интерференция только |
|||||||||
когерентных волн с одинаковой частотой, направления колебаний которых |
|||||||||
совпадают. Под когерентностью волн понимается постоянство разности |
|||||||||
фаз. Рассмотрим интерферен- |
S2 |
|
|
|
Э |
||||
цию двух световых волн. |
|
|
|
|
|||||
Пусть два точечных и |
с- |
|
|
|
|
l 2 |
|||
точника света S1 и S2, пока- |
|
|
|
|
|||||
занных на рисунке 3.1, излу- |
|
|
n2 |
P |
|||||
чают |
монохроматические |
|
|
n1 |
|||||
плоско-поляризованные свето- |
|
|
|
||||||
вые волны с одинаковой час- |
|
|
|
|
l 1 |
||||
тотой ω и нулевой начальной |
S1 |
|
|
|
|||||
|
|
|
|
||||||
фазой |
α1 =α2 = 0 . |
Причем, |
|
|
|
|
|
||
пусть плоскости поляризации |
Рисунок 3.1 – Схема получения |
||||||||
совпадают. Определим интен- |
|||||||||
интерференционной картины от |
|||||||||
сивность света IP |
в точке эк- |
||||||||
двух точечных источников |
|||||||||
рана Р в результате сложения |
|||||||||
|
|
|
|
|
|||||
световых волн от первого и второго источников света в момент времени t . |
|||||||||
Колебания напряженности электрического поля E1,P (в плоскости коле- |
|||||||||
баний) в точке Р, создаваемые |
световой |
волной, |
испускаемой первым |
||||||
источником света S1,определяются выражением: |
|
||||||||
|
|
|
E1,P = E01sin(ω(t −t1 )) , |
|
|||||
24 |
|
|
|
|
|
|
|
|
|

где E01 – амплитуда колебаний напряженности электрического поля в световой волне, излучаемой источником S1; t1 – время, за которое волна
проходит от источника света S1 до точки Р. Аналогично, колебания напряженности электрического поля E2,P в точке Р, создаваемые световой
волной, испускаемой источником света S2 , определяются выражением:
E2,P = E02sin(ω(t −t2 )),
где E02 – амплитуда колебаний напряженности электрического поля в световой волне, излучаемой источником S2; t2 – время, за которое свет от
источника света S2 достигает точки Р. Учитывая, что свет от первого источника распространяется в среде с показателем преломления n1 , а свет
от второго источника – в среде с показателем n2 , значения t1 и t2 можно найти по формулам:
t = |
l 1 |
= |
l 1 |
n , |
t |
|
= |
l 2 |
= |
l 2 |
n |
|
, |
|
|
|
|
|
|||||||||||
v |
c |
|
|
c |
|
|||||||||
1 |
|
1 |
|
2 |
|
v |
2 |
|
|
2 |
|
|||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
где l 1 и l 2 – расстояния от источников S1 |
и S2 до точки наблюдения Р; v1 |
|||||||||||||
и v2 – фазовая скорость света в среде с показателем преломления n1 и n2
соответственно; c – скорость света в вакууме. Таким образом, разность фаз δP колебаний, создаваемых волнами, излучаемыми источниками S1 и
S2 в точке Р, равна:
δ |
P |
= |
ω (l |
1 |
n −l |
n |
2 |
). |
(3.3) |
|
|
c |
1 |
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
Произведение расстояния, пройденного электромагнитной волной в среде, на показатель преломления этой среды называется оптической длиной пути. Учитывая, что ω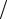 c = 2π
c = 2π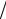 λ (λ – длина волны в вакууме), выраже-
λ (λ – длина волны в вакууме), выраже-
ние (2.3) можно переписать в виде:
δP = 2λπ ∆,
где ∆ =(l 1n1 −l 2n2 ) – оптическая разность хода.
Если оптическая разность хода ∆ равна целому числу длин волн λ, то есть
∆ =± m λ |
(m = 0,1, 2,K ), |
(3.4) |
то разность фаз δP кратна 2π и лучи приходят в точку Р с одинаковой
фазой. При выполнении условия (3.4) интенсивность света в точке Р будет иметь максимальное значение Imax , равное, согласно формуле (3.2),
Imax = I1 + I2 + 2
 I1 I2 ,
I1 I2 ,
где I1 и I2 – интенсивности света, испускаемого источниками S1 и S2. Если оптическая разность хода ∆ равна полуцелому числу длин волн λ :
|
1 |
|
λ |
(m = 0,1, 2,K ), |
(3.5) |
∆ =± m + |
2 |
|
|||
|
|
|
|
|
то разность фаз δP равна нечетному числу π и лучи приходят в точку Р в
25
противофазе, и результирующая интенсивность света будет минимальна:
Imin = I1 + I2 − 2
 I1 I2 .
I1 I2 .
Выражения (3.4) и ( 3.5) называются условиями интерференционного максимума и минимума соответственно.
Из проведенного анализа следует, что интенсивность света на экране Э при сложении волн, испускаемых источниками S1 и S2 , может принимать значения в диапазоне от Imin до Imax . Значение интенсивности в
конкретной точке будет определяться оптической разностью хода световых волн. Таким образом, в результате интерференции световых волн, излучаемых источниками света S1 и S2 , на экране Э будет наблюдаться чередование светлых и темных полос. Описанное распределение интенсивности называется интерференционной картиной.
3.2.3 Интерферометр Рэлея
Интерференционная картина чрезвычайно чувствительна к малейшим изменениям условий ее получения. Незначительное изменение оптической разности хода (порядка долей длины волны) может привести к существенному изменению интерференционной картины (смещению полос). Это свойство используется для создания специальных приборов – интерферометров, основанных на зависимости интерференционной картины и позволяющих проводить очень точные измерения. Интерферометр Майкельсона позволяет с точностью до 10–7м определять длины. Интерферометр Линника позволяет исследовать качество обработки поверхностей. Интерферометр Жамена позволяет измерять близкие к единице показатели преломления. Для анализа газов или жидкостей применяется интерферометр Рэлея, принципиальная схема которого приведена на рисунке 3.2.
L1 C |
A |
L2 |
|
1 |
|
|
|
3 |
O |
S |
|
|
4 |
|
|
B |
2 |
|
K |
|
|
|
|
|
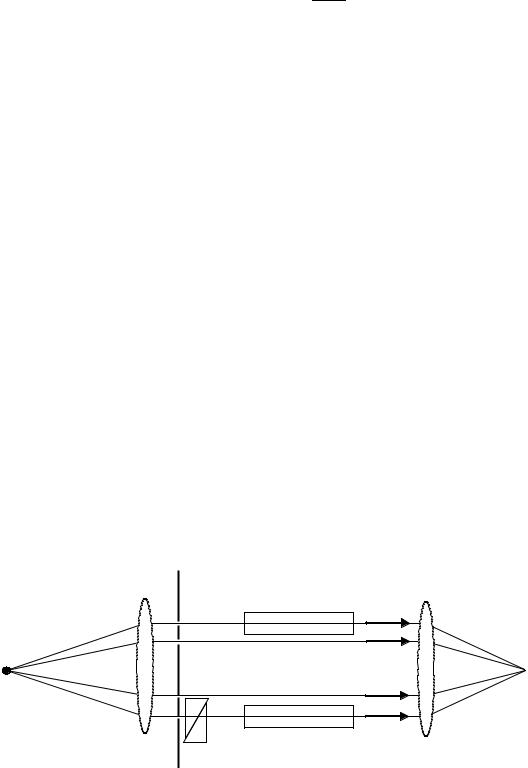
Рисунок 3.2 – Оптическая схема интерферометра Рэлея
Свет, излучаемый источником S, проходя через линзу L1 щели С, разделяется на четыре параллельных луча. Лучи 1 и 2 проходят через одинаковые кюветы: А – заполненную исследуемым веществом, и В – заполненную веществом с известным показателем преломления. Кроме
26
этого, луч 2 проходит через клиновой компенсатор К. Лучи 3 и 4 проходят мимо камер А и В. Все лучи попарно (первый со вторым, третий с четвертым) собираются линзой L2 и создают в разделенном пополам объективе О две интерференционные картины, показанные на рисунке 3.3. Положение интерференционных полос, создаваемых третьим и четвертым лучами, постоянно. Различие показателей преломления веществ в кюветах приводит к появлению оптической разности хода ∆:
∆ = (nA −nB )d , |
(3.6) |
где nA и nB – показатели преломления веществ, заполняющих кюветы А и |
||
|
В; d – длина кюветы. Появление оптической |
|
|
разности хода приводит к смещению создава- |
|
|
емой первым и вторым лучами интерфе- |
|
|
ренционной картины, измеряя величину откло- |
|
|
нения которой, можно найти показатель пре- |
|
|
ломления исследуемого вещества. Для изме- |
|
|
рения величины ∆ служит клиновой компен- |
|
|
сатор К, состоящий из двух клиньев, образу- |
|
Рисунок 3.3 – Интерфе- |
ющих плоскопараллельную пластину. Сдвигая |
|
один из клиньев относительно другого, можно |
||
ренционные картины |
установить такую толщину l |
получающейся |
|
||
|
плоско-параллельной пластинки, что создавае- |
|
мая ею разность оптического хода будет компенсировать разность хода ∆, |
||
создаваемую кюветами. В этом случае интерференционные картины, соз- |
||
даваемые различными лучами, совпадут. Таким образом, зная показатель |
||
преломления вещества, из которого сделан компенсатор |
nK и длину l , |
|
можно рассчитать величину |
|
|
∆= nK l ,
азатем из формулы (3.6) найти показатель преломления исследуемого
вещества.
3.3 Вывод рабочих формул
3.3.1 Формула для вычисления показателя преломления растворенного вещества
Согласно классической электронной теории дисперсии, величина r , называемая удельной рефракцией, является постоянной для каждого вещества. Связь удельной рефракции вещества с его показателем преломления n определяется формулой Лоренц-Лорентца:
r = |
n2 |
−1 |
|
1 |
, |
(3.7) |
|
n2 + 2 |
ρ |
||||||
|
|
|
|
||||
где ρ – плотность вещества. Опыт показывает, что удельная рефракция смеси двух веществ R , имеющих удельные рефракции r1 и r2 , равна:
R =C1r1 +C2r2 , |
(3.8) |
27

где C1 и C2 – объемная доля первого и второго веществ в растворе.
Учитывая, что объемной долей вещества в растворе называется отношение объема, занимаемого молекулами данного вещества, к полному объему раствора, верно соотношение:
1 = |
V1 |
+ |
V2 |
|
=C +C |
2 |
, |
|
|
|
|||||
V1 +V2 |
|
1 |
|
||||
V1 +V2 |
|
|
|||||
где V1 и V2 – объемы, занимаемые молекулами первого и второго вещест- |
|||||||
ва. Тогда выражение (3.8) можно переписать в виде: |
|
||||||
|
R =(1−C2 )r1 +C2 r2 . |
|
(3.9) |
||||
Пусть известны показатель преломления раствора n , растворителя n1, |
|||||||
плотности растворенного вещества |
ρ2 , |
растворителя ρ1 и объемная доля |
|||||
растворенного вещества C2 . Получим выражение для показателя преломления растворенного вещества n2 . Из формулы Лоренца-Лорентца (3.7)
выразим n2 через удельную рефракцию r2 : |
|
|
|
|
|
|
|
|||||||||||
n |
= |
|
|
|
1+ 2 r2 ρ2 |
|
. |
(3.10) |
||||||||||
|
|
|
|
|
||||||||||||||
2 |
|
|
|
|
|
1−r2 ρ2 |
|
|||||||||||
Значение удельной рефракции r2 |
|
|
|
|
|
|
||||||||||||
растворенного вещества можно найти из |
||||||||||||||||||
выражения (3.9): |
|
R −(1−C2 )r1 |
|
|
||||||||||||||
r = |
. |
(3.11) |
||||||||||||||||
|
|
|
|
|
|
|||||||||||||
2 |
|
|
|
|
|
|
C2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Значения удельных рефракций раствора R и растворителя r1 |
определяются |
|||||||||||||||||
соотношениями: |
|
|
|
n2 |
−1 1 |
|
|
|
|
|
|
|||||||
R = |
, |
|
|
|
(3.12) |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
n2 |
+ 2 ρ |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
r |
= |
|
n2 |
−1 |
1 |
|
. |
|
|
|
(3.13) |
|||||||
1 |
|
|
|
|
|
|
|
|
|
|||||||||
1 |
|
n2 |
+ 2 |
|
ρ |
1 |
|
|
|
|
|
|
||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||
Плотность раствора ρ определяется выражением: |
|
|||||||||||||||||
ρ =(1−C2 )ρ1 +C2 ρ2 . |
(3.14) |
|||||||||||||||||
3.4 Экспериментальная часть
3.4.1 Безопасность труда
В работе используется интерферометр ЛИР–2, подключаемый к сети переменного тока 220 В. При выполнении работы необходимо надежно заземлить приборы.
3.4.2 Приборы и принадлежности
Интерферометр ЛИР–2 с набором кювет, исследуемые растворы, дистиллированная вода, пипетки.
28
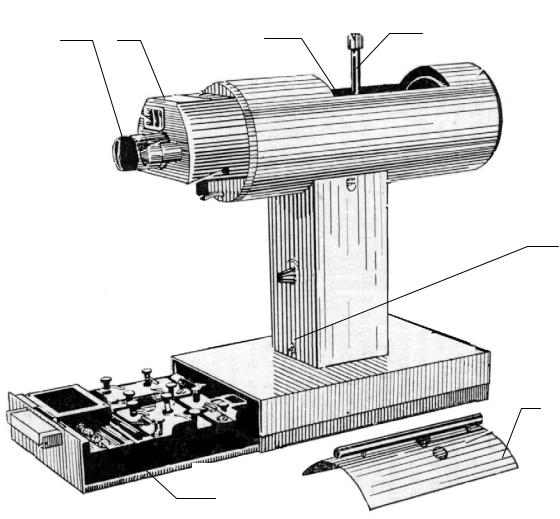
3.4.3 Описание интерферометра ЛИР–2
Интерферометр ЛИР–2 представляет собой лабораторный прибор для определения показателя преломления жидкостей, показанный на рисунке 3.4. В верхней части прибора находится термокамера 3, в которую помещаются кюветы с исследуемым веществом. Камера закрывается крышкой 6. Ручка 4 позволяет приводить в действие мешалку, предназначенную для ускорения процесса установления термодинамического равновесия. Через зрительный окуляр 1 можно наблюдать две: подвижную и неподвижную интерференционные картины. Совмещение интерфе-
|
1 |
|
2 |
3 |
4 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
5
6
7
1 – зрительный окуляр; 2 - лупа для снятия показаний микрометрического
винта; 3 – термокамера; 4 – ручка мешалки; 5 – тумблер включения прибора; 6 – крышка термокамеры; 7 – выдвижной ящик с принадлежностями
Рисунок 3.4 - Интерферометр Рэлея ЛИР–2
ренционных картин осуществляется с помощью перемещения подвижного клина в клиновом компенсаторе. Перемещение клина осуществляется поворотом проградуированного микрометрического винта, расположен-
29
ного с левой стороны прибора. Над окуляром, для удобства снятия отсчета, находится лупа 2. Микрометрический винт проградуирован на 3000 делений: 100 делений на барабане и 30 делений на стебле (одно деление на стебле соответствует сотне делений на барабане). Микрометрический винт проградуирован так, что поворот на одно деление вносит дополнительную разность хода:
∆ = |
λ |
, |
(3.15) |
|
|||
1 |
30 |
|
|
|
|
|
где λ = 550 10−9 м – длина световой волны, для которой человеческий глаз наиболее чувствителен. Включение прибора осуществляется тумблером 5.
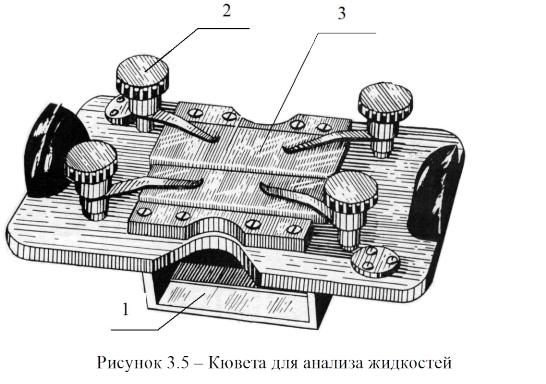
В основании прибора имеется выдвижной ящик 7, в котором находятся кюветы, показанные на рисунке 3.5, с различным размером камер 5, 10, 20, 40 и 80 мм. Кюветы состоят из двух камер 1, закрытых сверху крышками 3. Крышки удерживаются прижимами 2.
Камеры кювет обозначены буквами «П» и «Л». При помещении кюветы в термокамеру интерферометра камера «П» должна распола-
гаться справа от наблюдателя, а «Л», соответственно, слева, при этом раствор с меньшим показателем преломления должен помещаться в левую камеру.
Внимание! Во время работы кюветы можно ставить только на специальную подставку. Ставить кюветы на стол категорически запрещается, так как в результате возможно загрязнение поверхности камер или термокамеры.
30
3.5 Порядок выполнения работы
3.5.1 Включить интерферометр в сеть переменного тока 220 В.
3.5.2 Заполнить термостатирующую камеру дистиллированной водой. 3.5.3 Заполнить на ¾ обе камеры кюветы длиной 10 мм дистиллированной водой и установить кювету в термокамеру. Интерферометр Рэлея является очень чувствительным прибором, поэтому незначительные флуктуации плотности жидкости вследствие неоднородности температуры приводят к искажению интерференционной картины. Во избежание этого, после установления кюветы в термокамеру, следует 1-2 минуты перемешивать жидкость с помощью мешалки для установления теплового
равновесия и только затем снимать показания.
3.5.4 Снять нуль кюветы N0 (т.е. показания барабана, при котором интерференционные картины совпадают) и занести полученный результат в таблицу 3.1. Обратить внимание, что если барабан ушел вправо за нулевое деление на стебле, результат получится отрицательный. При этом показания надо считать по-другому. Правильный отсчет получается, если отнять от 100 текущее показание на барабане. Например, если на барабане 86, то правильный результат, который нужно занести в таблицу:
–14.
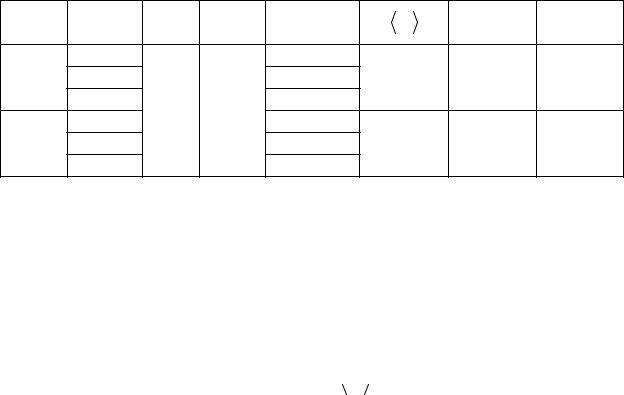
Таблица 3.1 – Результаты измерений |
|
|
|
|
|||
C2 |
Номер |
d, м |
N0 |
N |
N |
∆ |
n |
опыта |
|||||||
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
0.01 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3.5.5 Налить в правую камеру кюветы первый исследуемый раствор, а в левую камеру – дистиллированную воду. При смене раствора в камере необходимо ее три раза ополоснуть новым раствором. Все операции по наполнению камер необходимо осуществлять пипеткой с резиновой грушей.
После установления теплового равновесия три раза снять показания N и занести данные в таблицу 3.1.
3.5.6 Повторить операцию для всех растворов.
3.5.7 Рассчитать среднее значение 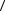 N
N 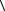 для каждого исследуемого
для каждого исследуемого
раствора. Рассчитать оптическую разность хода ∆, возникающую в результате различия показателей преломления дистиллированной воды и исследуемого раствора по формуле:
∆ = ∆1( N
N  − N0 ),
− N0 ),
31
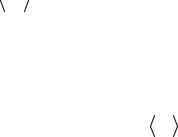
где ∆1 – оптическая разность хода, создаваемая при повороте микромет-
рического винта на одно деление, определяемая выражением (3.15). Затем по формуле (3.6) рассчитать показатели преломления n каждого исследуемого раствора. Результаты расчетов занести в таблицы 3.1 и 3.2.
3.5.8 По данным таблицы 3.1 построить зависимость показателя преломления раствора от концентрации растворенного вещества. По графику определить неизвестную концентрацию.
3.5.9 Найти показатель преломления растворенного вещества. Для этого для каждого исследуемого раствора (водного раствора этилового спирта) определить по формуле (3.14) плотность раствора ρ и занести в
таблицу 3.2. Затем по формулам (3.12) и (3.13) рассчитать удельные рефракции дистиллированной воды r1 и каждого исследуемого раствора R.
Полученные значения занести в таблицу 3.2. По формуле (3.11) найти рефракцию r2 растворенного вещества (этилового спирта) и по формуле (3.10) рассчитать показатель его преломления n2. Найти среднее
значение показателя преломления этилового спирта 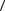 n2
n2  и сравнить его с табличным значением.
и сравнить его с табличным значением.
Таблица 3.2 – Результаты расчета показателя преломления растворенного
вещества
n |
n1 |
C2 |
ρ1 , |
кг |
ρ2 , |
кг |
ρ, |
кг |
r1 |
R |
r2 |
n2 |
n2 |
|
|
|
|
м3 |
|
м3 |
|
м3 |
|
|
|
|
|
|
1.333 |
|
1000 |
791 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.5.10 Оценить погрешность проделанных вычислений.
3.5.11 По результатам проделанной работы сделать вывод.
3.6 Контрольные вопросы
3.6.1 Какое явление называется интерференцией?
3.6.2 Каковы условия наблюдения явления интерференции?
3.6.3 Какие световые волны называются когерентными?
3.6.4 Объяснить усиление или ослабление интенсивности света при сложении когерентных колебаний.
3.6.5 Написать условия максимума и минимума интенсивности света при сложении когерентных световых волн.
3.6.6 Какие приборы называются интерферометрами?
3.6.7 Для чего предназначен интерферометр Рэлея?
3.6.8 Описать принципиальное устройство интерферометра Рэлея.
3.6.9 Как с помощью интерферометра Рэлея определить показатель
32
преломления жидкости?
3.6.10 Привести расчетные формулы для показателя преломления растворенного вещества.
Литература
1Савельев И.В. Курс общей физики / И.В. Савельев: учебное пособие:
в5 т.– М.: Наука, 2002. – Т.3.
2Путилов К.А. Курс физики / К.А. Путилов, В.А. Фабрикант – М.: Физматгиз, 1963. – Т.3
3Ландсберг Г.С. Оптика / Г.С. Ландсберг – М.: Госиздат технико– теоретической литература, 1957.
4Корякин Н.И. Краткий справочник по физике / Н.И.Корякин, К.Н Быстров, П.С., Киреев– М.: Высшая школа, 1964.
33
4 Определение длин световых волн с помощью дифракционной решетки
4.1 Цель работы
Изучение дифракции Фраунгофера на дифракционной решётке и определение с её помощью длин световых волн.
4.2 Теоретическое введение
4.2.1 Дифракция света
Дифракцией света называется отклонение световых лучей от прямолинейного пути при прохождении вблизи краёв экранов, отверстий (или других неоднородностей).
Явление дифракции указывает на нарушение законов геометрической оптики.
Дифракция света обусловлена его волновой природой. Она может наблюдаться, если величина препятствий на пути света соизмерима с длинами световых электромагнитных волн.
Дифрагированные лучи являются когерентными, а поэтому дифракция, как правило, сопровождается интерференционными явлениями [1].
Решение задачи дифракции заключается в нахождении распределения на экране интенсивности световой волны в зависимости от размеров и формы препятствий. Строгое математическое решение такой задачи на основе электромагнитной теории Максвелла является сложным. Однако оно может быть сведено к приближённым методам, основанным на принципах Гюйгенса и Гюйгенса-Френеля.
Принцип Гюйгенса: каждая точка, до которой доходит волновое движение, является источником новых, вторичных волн; огибающая этих волн даёт положение фронта волны в следующий момент времени.
Пусть на плоскую преграду с отверстием падает параллельный ей фронт волны, как показано на рисунке 4.1. По Гюйгенсу каждая точка выделяемого отверстием участка волнового фронта служит источником вторичных волн, которые в однородной и изотропной среде будут сферическими. Построив огибающую вторичных волн, мы убеждаемся в том, что за отверстием волна проникает в область геометрической тени (на рисунке границы этой области показаны штриховыми линиями), огибая края преграды.
Однако принцип Гюйгенса не даёт сведений об амплитуде, а следовательно, и об интенсивности волн, распространяющихся в различных направлениях. Френель дополнил этот принцип представлением об интерференции вторичных волн. Учёт амплитуд и фаз вторичных волн
34

позволяет найти амплитуду результирующей волны в любой точке пространства.
Область |
Область |
|
|
геометрической |
|
||
геометрической |
|
||
тени |
|
||
тени |
|
||
|
|
||
Рисунок 4.1 – К принципу Гюйгенса |
Рисунок 4.2 – Дифракция |
||
Фраунгофера |
|||
|
|
||
Принцип Гюйгенса-Френеля: все вторичные источники, расположенные на поверхности фронта волны, когерентны между собой. Амплитуда и фаза волны в любой точке пространства – это результат интерференции волн, излучаемых вторичными источниками.
Наблюдение дифракции осуществляется обычно по следующей схеме. На пути световой волны, распространяющейся от некоторого источника, помещается непрозрачная преграда, закрывающая часть волновой поверхности (множество точек пространства, в которых колебания совершаются в одной фазе) световой волны. За преградой располагается экран, на котором возникает дифракционная картина.
Различают два вида дифракции. Если источник света S и точка наблюдения P расположены от препятствия настолько далеко, что лучи, падающие на препятствие, и лучи, идущие в точку P, образуют практически параллельные пучки, говорят о дифракции в параллельных лучах или о дифракции Фраунгофера. В противном случае говорят о
дифракции Френеля. Дифракцию Фраунгофера можно наблюдать, поместив за источником света S и перед точкой наблюдения P по одной линзе так, чтобы точки S и P оказались в фокальной плоскости соответствующей линзы, как показано на рисунке 4.2. В дальнейшем будет рассматриваться лишь дифракция Фраунгофера.
4.2.2 Дифракция света на щели
Рассмотрим узкую щель шириной BC = a, освещаемую пучком параллельных монохроматических лучей с длиной волны λ, показанную на рисунке 4.3. Согласно принципу Гюйгенса, каждая из освещённых точек щели становится источником колебаний – центром новых вторичных волн. Эти волны распространяются в пространстве за щелью во всех направлениях. В фокальную плоскость линзы Л, поставленной перед экраном Э, лучи будут попадать от разных точек щели, то есть они будут иметь разность хода и, следовательно, интерферировать. На экране волны могут встретиться в одинаковых фазах – тогда происходит усиление
35

колебаний, в разных – ослабление колебаний. Все лучи, идущие от щели, можно мысленно разделить на системы параллельных лучей. Лучи каждой из систем образуют с нормалью к плоской щели определённый угол φ (угол дифракции) и собираются линзой в определённой точке Pφ . Оптическая разность хода между крайними лучами ВМ и СN, идущими от щели в произвольном направлении ϕ, равна
= СD = a sinϕ,
где D − основание перпендикуляра, опущенного из точки В на луч СN, а абсолютный показатель преломления воздуха считается равным единице.
|
а |
В |
|
С |
D |
В |
С |
|
а |
b |
|
|
φ |
φ |
К |
φ |
|
φD
М |
N |
|
Л |
М |
N |
0 |
Л |
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Э |
|
Pφ |
Pо |
Э |
Pφ |
Pо |
|
|
||||
|
|
|
|
|
|||
Рисунок 4.3 –Дифракция на щели |
Рисунок 4.4 – Дифракция на решётке |
||||||
Разобьем щель ВС на зоны Френеля, имеющие вид полос, параллельных ребру В щели. Ширина каждой зоны выбирается так, чтобы разность хода от краев этих зон была равна λ/2, то есть всего на ширине щели уместится /(λ/2) зон. Так как свет на щель падает нормально, то плоскость щели совпадает с волновым фронтом; следовательно, все точки волнового фронта в плоскости щели будут колебаться в одинаковой фазе. Амплитуды вторичных волн плоскости щели будут равны, так как выбранные зоны Френеля имеют одинаковые площади и одинаково наклонены к направлению наблюдения. При интерференции света от каждой пары соседних зон амплитуда результирующих колебаний равна нулю, так как эти зоны вызывают колебания с одинаковыми а мплитудами, но противоположными фазами. Таким образом, результат интерференции света в точке Рϕ определяется тем, сколько зон Френеля укладывается в щели. Если число зон нечетное, то есть
a sinϕ = ± (2k + 1) λ/2 |
(k = 1, 2, …), |
(4.1) |
36
то наблюдается дифракционный максимум, соответствующий действию одной нескомпенсированной зоны Френеля. Знак минус в правой части формулы (4.1) соответствует лучам света, распространяющимся от щели под углом -ϕ и собирающимся в побочном фокусе Р-ϕ линзы Л,
симметричном с Рϕ относительно главного фокуса Ро. Если число зон четное, то есть
a sinϕ = ± 2kλ/2 |
(k = 1, 2, …), |
(4.2) |
то наблюдается дифракционный минимум (полная темнота).
В направлении ϕ , равного 0, наблюдается самый интенсивный
центральный максимум нулевого порядка. В точке Ро (ОРо −
оптическая ось линзы) всегда наблюдается усиление света, независимо от длины волны λ. По обе стороны от центрального (нулевого) максимума располагаются чередующиеся между собой min и max 1-го , 2-го и т. д. порядков.
Заметим, что расчет дифракционной картины, основанный на использовании метода зон Френеля, является приближенным. Точное решение этой задачи осуществляется путем разбиения щели на бесконечное число одинаковых бесконечно узких полос, параллельных ребру В [1].
При наблюдении дифракции на щели в белом свете интерференционная картина на экране оказывается окрашенной. В дифракционном максимуме каждого порядка (k=const) ближе к центральному, неокрашенному максимуму оказываются, в соответствии с формулой (4.1), дифракционные максимумы с меньшими длинами волн.
4.2.3 Дифракция света на дифракционной решётке
Простейшей дифракционной решёткой является система из N одинаковых параллельных щелей в плоском непрозрачном экране, шириной a каждая, расположенных на равных непрозрачных промежутках b друг от друга, как видно из рисунка 4.4. Величина d, равная a+b,
называется постоянной (периодом) дифракционной решётки.
По принципу Гюйгенса-Френеля каждая щель является источником когерентных вторичных волн, способных интерферировать друг с другом. Если на дифракционную решётку перпендикулярно к ней падает пучок параллельных лучей света, то под углом дифракции φ на экране Э, расположенном в фокальной плоскости линзы, будет наблюдаться система дифракционных максимумов и минимумов, полученная в результате интерференции света от различных щелей.
Главные максимумы при дифракции на решётке наблюдаются под углами φ, удовлетворяющими условию:
d sin φ = ± kλ, |
(4.3) |
37

где k = 0, 1, 2, 3… называется порядком главного максимума. Величина Δ=DK=d sin φ является оптической разностью хода между сходственными лучами BM и DN , идущими от соседних щелей (см. рисунок 4.4).
Главные минимумы на дифракционной решётке наблюдаются под такими углами φ дифракции, для которых свет от разных частей каждой щели полностью гасится в результате интерференции. Условие главных минимумов совпадает с условием (4.2) ослабления на одной щели:
a sin φ = ±2k |
л |
(k = 1, 2, 3,…). |
2 |
В теории дифракции доказывается, что если решётка имеет N щелей, то между двумя соседними главными максимумами расположено N-1 дополнительных минимумов. Между каждыми двумя соседними дополнительными минимумами имеются, естественно, слабые дополнительные максимумы, которые создают весьма слабую освещённость – фон, на котором чётко видны главные максимумы, как показано на рисунке 4.5.
Возникновение добавочных минимумов при дифракции на большом числе щелей приводит к тому, что главные максимумы становятся более узкими и яркими, происходит концентрация световой энергии в направлениях, соответствующих главным максимумам. Усиление яркости при увеличении числа щелей происходит ещё и потому, что увеличивается общая площадь прозрачных промежутков.
I |
0 max |
-1 max |
1 max |
-2 max |
2 max |
-2 |
л |
- |
л |
0 |
л |
2 |
л |
|
d |
d |
d |
d |
|||||
|
|
|
|
Рисунок 4.5 – Распределение интенсивности света в спектре
дифракционной решётки
Амплитуды колебаний, исходящих от всех N щелей решётки в направлениях усиления, складываются. Амплитуда результирующего колебания получается в N раз больше амплитуды колебания от одной щели, а результирующая интенсивность в N2 раз больше интенсивности нулевого максимума от одной щели, так как интенсивность света пропорциональна квадрату амплитуды. Резкость максимумов обеспечивает возможность надёжно отличать близкие длины волн λ1 и λ2 , которые изображаются раздельными яркими полосками, а не перекрывают друг
38

друга, как это имеет место при расплывчатых максимумах, получающихся от одной щели, или малого их числа. Это свойство дифракционной решётки используется для исследования спектрального состава света (определения длин волн и интенсивностей всех монохроматических компонентов), то есть дифракционная решётка может быть использована как спектральный прибор.
Разрешающей силой спектрального прибора называют величину
R = л2 л2 л1 = длл2 .
Разрешающая сила дифракционной решётки пропорциональна порядку спектра k и числу щелей N [1]:
R = kN .
При освещении решётки с большой разрешающей силой белым светом в центре экрана возникает белая полоса (нулевой максимум, отвечающий φ=0 для всех длин волн). Справа и слева от центральной полосы располагаются спектры в виде чётких цветных полос, разделённых тёмными промежутками, так как каждому цвету с длиной волны λ соответствует свой угол дифракции (формула (4.3)). Причём, чем меньше длина волны, тем меньшему значению угла φ соответствует положение максимума. Таким образом, белый свет разлагается дифракционной решёткой в спектр так, что цвета в нём располагаются от внутреннего края к внешнему в порядке возрастания длины волны, то есть фиолетовый, синий, голубой, зелёный, жёлтый, оранжевый, красный, как видно из рисунка 4.6. Спектры разделены тёмными полосами, соответствующими минимумам интенсивности света.
|
k = -2 |
|
k = -1 |
k = 0 k = 1 |
|
k = 2 |
|||||||
Спектр |
|
Спектр |
Белая |
Спектр |
|
|
Спектр |
||||||
|
1 |
го |
по- |
1 |
го |
по- |
|
|
|||||
2 |
го |
порядка |
|
поло- |
|
2 |
го |
порядка |
|||||
|
рядка |
са |
рядка |
|
|||||||||
Кр |
|
|
Ф Кр |
Ф |
Ф |
|
|
Кр Ф |
|
Кр |
|||
Рисунок 4.6 – Дифракционный спектр
Если разрешающая способность дифракционной решётки невелика, главные максимумы становятся расплывчатыми, спектры 1-го и 2-го порядков оказываются сплошными, а спектры более высоких порядков вообще не удаётся разглядеть из-за их перекрывания.
Дифракционные спектры во многом отличаются от дисперсионных [2]. Основное различие состоит в следующем:
39
1)в дифракционном спектре ближе к центральной белой полосе располагаются фиолетовые линии, дальше − красные, а в дисперсионном наоборот;
2)в дифракционном спектре низкого порядка (k=1,2) углы дифракции прямо пропорциональны длинам волн, что обеспечивает равномерность спектра. В дисперсионном спектре равномерность отсутствует (красная область спектра сжата), так как дисперсия больше в коротковолновой части.
4.3 Описание установки
Внешний вид установки для определения длин волн изображён на рисунке 4.7.
При работе с дифракционной решёткой главной задачей является точное измерение углов, на которых наблюдаются главные максимумы для различных длин волн. Измерения этих углов удобно проводить с помощью гониометра – прибора, предназначенного для точного измерения углов.
1 |
2 |
3 |
4 |
5 |
6 |
7 |
9 |
8 |
Лимб
Нониус
1–окуляр; 2–зрительная труба; 3–дифракционная решётка; 4–столик; 5– коллиматор; 6–щель коллиматора; 7–источник света; 8–лимб; 9–нониус
Рисунок 4.7 – Лабораторная установка
Основными частями прибора являются зрительная труба 2 и коллиматор 5, служащий для получения параллельного пучка лучей. Коллиматор – металлическая труба, с одной стороны которой установлен объектив, с другой – щель 6. Щель расположена в фокальной плоскости и обращена к источнику света. Ширина щели регулируется при помощи микрометриического винта. Лучи света источника 7, прошедшие коллиматор, выходят из него параллельным пучком и, падая на объектив трубы (коллиматорная
40
и зрительная трубы должны быть центрированы), собираются в его фокальной плоскости, давая изображение щели. В фокальной плоскости объектива зрительной трубы расположена вертикальная визирная нить. Так что в поле зрения окуляра 1 зрительной трубы видны одновременно нить и изображение щели.
Зрительная труба может поворачиваться относительно лимба 8. Лимб представляет собой горизонтально расположенный металлический диск, на котором нанесены деления в градусах. Одновременно со зрительной трубой поворачивается круговой нониус 9, скреплённый с трубой неподвижно. При помощи нониуса производится отсчёт положения трубы относительно лимба. Круговой нониус представляет собой небольшую дуговую линейку, скользящую вдоль круга лимба, разделённую на градусы или на ещё более мелкие части. Точность кругового нониуса может быть определена, если известно наименьшее деление лимба и число делений нониуса. Например, если наименьшее деление лимба
составляет 1o, а число делений нониуса равно 10, то точность нониуса будет равна:
1o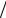 10 = 60'
10 = 60'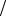 10 = 6'= 0.1o .
10 = 6'= 0.1o .
С лимбом центрирован столик 4, который может поворачиваться и подниматься; на него и устанавливается дифракционная решётка 3.
Принципиальная схема хода лучей в гониометре соответствует рисунку 4.2.
4.4 Указания по технике безопасности
Источник света подключён к трансформатору, на вход которого подаётся напряжение 220 В. Перед началом работы проверьте заземление трансформатора.
4.5 Порядок выполнения работы
4.5.1 Приборы и принадлежности: гониометр, источник света, дифракционная решётка.
4.5.2 Включить источник света; установить гониометр так, чтобы источник света находился на продолжении оси коллиматора.
4.5.3 Проверить резкость изображения щели и визирной линии в поле зрения зрительной трубы. Ширину щели сделать предельно узкой при достаточной интенсивности светового пучка. Ширина изображения щели не должна превышать 2мм.
41
4.5.4 Установить дифракционную решётку на столик гониометра так, чтобы её плоскость была перпендикулярна оси коллиматора; при этом штрихи решётки должны быть вертикальными.
4.5.5 Поворачивая зрительную трубу вправо и влево, просмотреть дифракционный спектр. Число k видимых порядков спектров с одной и с другой стороны от неотклонённого положения трубы должно быть не менее двух, спектральные линии должны быть видны резко и располагаться симметрично с обеих сторон.
4.5.6 Повернуть зрительную трубу вправо от центрального максимума (белой полосы в центре) и найти линии спектра первого поряд-
ка (k=1).
4.5.7 Совместить визирную линию с серединой фиолетовой полосы и снять отсчёт угла φ’1 по лимбу и нониусу. Значение угла φ’1 записать в таблицу 4.1. Аналогично выполнить измерения для зелёной и красной полос и результаты занести в таблицу 4.1.
4.5.8 Повернуть трубу дальше вправо и найти линии спектра второго порядка (k=2). Произвести отсчёт углов φ2’ для тех же полос, что и в спектре первого порядка и их значения занести в таблицу 4.1.
4.5.9 Повторить подобные измерения φk” для спектров первого и второго порядков по другую сторону (слева) от центрального (нулевого) максимума. Результаты записать в таблицу 4.1.
Таблица 4.1– Результаты измерений и вычислений
|
Цвет |
Положение цветной |
Угол |
Длина |
||
Порядок |
полосы |
волны |
||||
полос |
дифракции |
|||||
спектра |
|
|
линии |
|||
φk’, град |
φk”, град |
|||||
спектра |
φk, град |
|||||
|
|
(справа) |
(слева) |
|
λk, нм |
|
k=1 |
Ф |
|
|
|
|
|
З |
|
|
|
|
||
|
Кр |
|
|
|
|
|
k=2 |
Ф |
|
|
|
|
|
З |
|
|
|
|
||
|
Кр |
|
|
|
|
|
4.5.10 Записать величину периода решётки (она указана на её оправе).
4.6 Обработка результатов измерений
4.6.1 По данным таблицы определите угол дифракции
φk=(φk’-φk”)/2
42

для каждой линии дифракционных спектров 1-го и 2 -го порядков. Значения φk занести в таблицу 4.1.
4.6.2 Используя формулу (4.3) дифракционной решётки, вычислить длины волн фиолетовой, зелёной, красной линий спектров
лk = |
d sin цk |
(k=1, 2) |
(4.4) |
|
k |
||||
|
|
|
и результаты записать в таблицу 4.1.
4.6.3 Найти среднее значение длин волн λф ср , λз ср ветствующие каждой из выбранных линий спектра. фиолетовых линий
и λкр ср , соотНапример, для
λф ср = λф1 + λф2 ,
2
где λф1 и λф2 – длины волн, соответствующие фиолетовым линиям спектров 1−го и 2−го порядков.
4.6.4 Подсчитать относительную и абсолютную погрешности измерения для каждой из найденных длин волн грубым методом расчёта [3], исходя из формулы (4.4), которую можно записать следующим образом:
λk = d sin ϕk '+ϕk " . k 2
Абсолютные погрешности ∆φk’ и ∆φk” следует выражать в радианах.
4.6.5 Записать выводы, в которых сравнить найденные на опыте длины волн спектральных линий с табличными значениями [2]. Окончательные результаты представить в виде
λ=(λср±∆λ), нм.
4.7 Контрольные вопросы
4.7.1 В чём заключается явление дифракции? 4.7.2 В чём состоит принцип Гюйгенса-Френеля? 4.7.3 Понятие о дифракции Фраунгофера.
4.7.4 Что называют постоянной дифракционной решётки?
4.7.5 Объяснить, как происходит дифракция на одной щели? Почему край спектра нулевого порядка при освещении щели немонохроматическим светом имеет цветную окраску?
4.7.6 Как происходит перераспределение потока световых волн на дифракционной решётке?
4.7.7 Дайте обоснование: а) условию главных максимумов; б) условию главных минимумов; в) условию дополнительных минимумов при дифракции на решётке.
43
4.7.8 Как образуются дифракционные спектры при падении на решётку монохроматического света? Белого света?
4.7.9 Чем отличаются спектры, полученные с помощью дифракционной решётки и призмы?
4.7.10 Разрешающая сила дифракционной решётки.
4.7.11 Написать уравнение, по которому будете рассчитывать длины волн линий спектра, полученного с помощью дифракционной решётки.
4.7.12 Вывести формулу для вычисления относительной погрешности измерения длины волны какой-либо линии дифракционного спектра.
Литература
1 Савельев И.В. Курс общей физики / И.В. Савельев: учебное пособие для втузов: в 5 кн.– 4-е изд. перераб. – М.: Наука. Физматлит, 1998. – Кн.4: Волны. Оптика. – 256 с.
2 Попов В.С. Исследование дисперсии стеклянной призмы: Руководство к лабораторной работе / В.С. Попов – Северск: СТИ ТПУ,
2001. – 19 с.
3 Погрешности измерений: Методические указания. – Томск: ТПИ.
1984. – 23 с.
44
5 Определение концентрации сахара сахариметром
5.1 Цель работы
Целью работы является изучение явлений поляризации света, вращения плоскости поляризации, двойного лучепреломления и практического применения этих явлений.
5.2 Теоретическое введение
Свет представляет собой физический объект сложной природы: в одних случаях он ведет себя как электромагнитная волна, в других – как поток особых частиц (фотонов).
Согласно волновым представлениям излучение светящегося тела слагается из большого числа плоскополяризованных электромагнитных волн, испускаемых отдельными его атомами. В электромагнитной волне
колеблются два вектора – вектор напряженности электрического поля E и
вектор напряженности магнитного поля H . Как показывает опыт, физиологическое, фотохимическое, фотоэлектрическое и другие действия
света вызываются колебаниями вектора E , поэтому его называют
световым вектором, а саму волну – световой волной. Световая волна, в
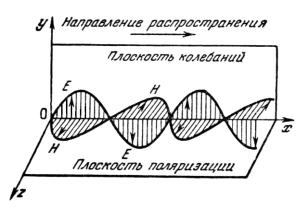
которой изменение вектора E происходит только в одной плоскости, называется плоскополяризованной волной. "Моментальная фотография" такой электромагнитной волны, излученной отдельным атомом, изображена на рисунке 5.1.
Рисунок 5.1 – " Моментальная фотография" электромагнитной волны
Плоскость, проходящая через направление колебания вектора E и направление распространения волны, называется плоскостью колебаний,
перпендикулярная к ней плоскость, в которой колеблется вектор H ,
называется плоскостью поляризации.
45
В естественном свете плоскости колебаний электромагнитные волн, испускаемых отдельными атомами, ориентированы случайным образом по отношению друг к другу. Поэтому в результирующей волне колебания различных направлений быстро и беспорядочно сменяют друг друга. Такой свет является неполяризованным.
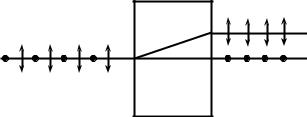
Плоскополяризованный свет можно получить различными способами, один из этих способов основан на явлении двойного лучепреломления, которое наблюдается в анизотропных средах. Анизотропной средой называется среда, физические свойства которой в различных направлениях различны. Анизотропной средой являются, например, кристаллы исланд-
ского шпата, кварца, турмалина. Явление двойного лучепреломления
заключается в том, что упавший на кристалл луч разделяется внутри кристалла на два луча, распространяющихся, вообще говоря, с разными скоростями и в различных направлениях, как показано на рисунке 5.2.
e
о
Рисунок 5.2 – Двойное преломление луча, падающего на анизотропный кристалл
При двойном лучепреломлении один из лучей подчиняется обычному закону преломления и лежит в одной плоскости с падающим лучом и нормалью к пр еломляющей поверхности. Этот луч называется обыкновенным и обозначается буквой о. Для другого луча, называемого необыкновенным (его обозначают буквой е), отношение синусов угла падения и угла преломления не остается постоянным при изменении угла падения. Даже при нормальном падении необыкновенный луч отклоняется от первоначального направления (см. рисунок 5.2). Необыкновенный луч не лежит, как правило, в одной плоскости с падающим лучом и нормалью к преломляющей поверхности. Оба вышедших из кристалла луча полностью поляризованы во взаимно перпендикулярных направлениях. В так называемых одноосных кристаллах имеется одно направление, вдоль которого о- и е- лучи распространяются не разделяясь и с одной и той же скоростью. Это направление называется оптической осью кристалла. Любая плоскость, проходящая через оптическую ось, называется главным сечением или главной плоскостью кристалла. В обыкновенном луче
колебания вектора E перпендикулярны главной плоскости кристалла (на рисунке 5.2 они обозначены точками), в необыкновенном – колебания совершаются в плоскости, совпадающей с главным сечением (изображены двухсторонними стрелками). Явление двойного лучепреломления наблюдается для всех прозрачных кристаллов, за исключением принадлежащих к
46
кубической системе. В анизотропных кристаллах диэлектрическая проницаемость ε для разных направлений имеет различные значения. Поэтому фазовая скорость световой волны
v = |
c |
= |
|
c |
|
, |
|
n |
|
|
|
||||
ε µ |
|||||||
|
|
|
|
|
где с – скорость света в вакууме, n – показатель преломления среды, а µ – относительная магнитная проницаемость среды, зависит от направления
колебаний светового вектора E и для о- и е- лучей принимает разные значения.
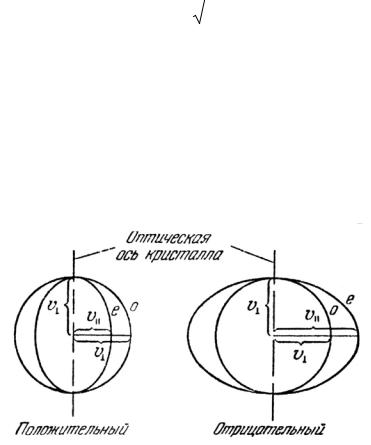
Изображая скорости о- и е- лучей в виде отрезков, отложенных по разным направлениям, можно построить волновые поверхности (поверхности равных фаз) обыкновенного и необыкновенного лучей, как видно из рисунка 5.3.
Рисунок 5.3 – Волновые поверхности о- и е- лучей
Волновая поверхность обыкновенных лучей представляет собой сферу, а необыкновенных – эллипсоид вращения. В местах пересечения с оптической осью кристалла сфера и эллипсоид соприкасаются. В зави-
симости от того, какая из скоростей vо или ve больше, различают положительные и отрицательные одноосные кристаллы. У положительных
кристаллов ve < vо , у отрицательных – ve > vо .
Зная вид волновых поверхностей, можно с помощью принципа Гюйгенса определить направления обыкновенного и необыкновенного лучей в кристалле [1]. На рисунке 5.4 построены волновые поверхности о- и е- лучей при нормальном падении света на преломляющую поверхность. Построение выполнено для момента времени, когда волновой фронт достиг поверхности кристалла. Огибающие для всех вторичных волн (волн, центры, которых лежат в промежутке между точками 1 и 2 на рисунке не показаны) для о- и е- лучей, очевидно, представляют собой плоскости. Преломленный луч о- или е-, выходящий, например, из точки 1, проходит через точку касания огибающей с соответствующей волновой поверхностью. Таким образом, если оптическая ось и поверх-
47

ность кристалла не лежат в одной плоскости, то даже при нормальном падении света на преломляющую поверхность необыкновенный луч отклонится от нормали к этой поверхности.
Рисунок 5.4 – Отклонение е- лучей от нормали к преломляющей поверхности при нормальном падении света на анизотропный кристалл
При выходе из кристалла оба луча отличаются друг от друга только направлением поляризации, поэтому названия “обыкновенный” и “необыкновенный” имеют смысл только для описания явлений внутри кристалла. Выделив один из двух преломленных лучей, можно получить плоскополяризованный свет. Прибор, с помощью которого получают поляризованную волну, называют поляризатором. Большое распространение получил поляризатор, называемый призмой Николя.
Призма Николя, показанная на рисунке 5.5, подставляет собой двойную призму из кристалла исландского шпата, склеенную в промежутке канадским бальзамом (по плоскости MP) [2].
Показатели преломления призмы Николя для обыкновенного и
необыкновенного лучей различны и равны no=1.659 и ne=1.486, соответственно. Канадский бальзам – смола канадской сосны, показатель преломления которой для λ=589 нм равен nб=1.549. Углы в призме подобраны таким образом, что обыкновенный луч падает на бальзам под углом падения большем предельного, в результате чего происходит полное внутреннее отражение. Отраженный луч (обыкновенный) поглощается зачерненной стенкой призмы (см. рисунок 5.5).
Рисунок 5.5 – Главное сечение призмы Николя
48
Для выявления поляризованного света используют приборы, получившие название анализаторов, которые по своему принципу действия аналогичны поляризаторам. Эти приборы свободно пропускают колебания, параллельные плоскости, которая называется плоскостью поляризатора, и полностью задерживают колебания, перпендикулярные этой плоскости. В приборах, предназначенных для исследования степени поляризации света, обычно используют две призмы Николя: одна служит поляризатором, другая – анализатором. В случае, когда плоскости главных сечений поляризатора и анализатора составляют произвольный угол ϕ, интенсивность света, прошедшего через поляризатор и анализатор определяется по закону Малюса
J = J0 cos2 ϕ , |
(5.1) |
где J0 – интенсивность плоскополяризованного света, падающего на
анализатор; J – интенсивность света, прошедшего через анализатор; ϕ – угол между плоскостями главных сечений поляризатора и анализатора.
Некоторые вещества обладают свойством поворачивать плоскость
колебаний вектора E вокруг луча. Такие вещества называются оптически активными. К ним относится кварц, киноварь, виннокаменная кислота, растворы некоторых веществ, например, раствор сахара. Величина угла
поворота плоскости колебаний для монохроматической волны λ = const пропорциональна концентрации оптически активного вещества C и толщине слоя L:
ϕ =α C L , |
(5.2) |
где С – концентрация растворённого вещества, численно равная отношению массы активного вещества в кг к весу раствора в кг (весовой процент); L – толщина слоя; α – удельная постоянная вращения –
физическая величина численно равная углу поворота плоскости колебаний при прохождении плоско поляризованного света через единицу толщины слоя оптически активного вещества концентрацией в единицу.
Угол вращения плоскости колебаний в слое определённой толщины зависит от концентрации раствора оптически активного вещества. Следовательно, по величине угла ϕ при L=const можно измерять концентрацию раствора.
49
5.3 Описание установки
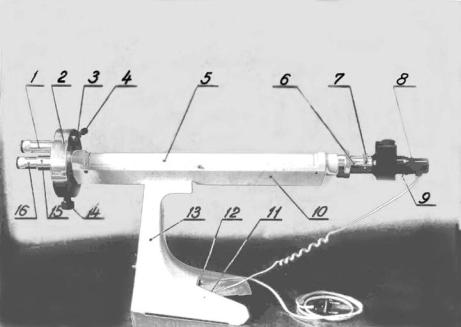
В данной работе используется прибор, называемый сахариметром универсальным типа СУ–3, внешний вид которого приведён на рисун-
ке 5.6 [3].
Рисунок 5.6 – Внешний вид сахариметра СУ-3
Основными частями прибора являются узел измерительной головки 2 и осветительный узел 8, соединённые между собой траверсой 10, на которой укреплена камера для поляриметрических кювет. С лицевой стороны измерительной головки прибора имеется лупа в оправе 1 для отсчёта показаний по шкале и зрительная труба 16. Зрительная труба имеет гильзу 15, снимающуюся при установке поля зрения на однородность. С тыльной стороны измерительной головки находится узел нониуса 3. В нижней части измерительной головки расположена рукоятка кремальерной передачи 14 для перемещения подвижного кварцевого клина и связанной с ним шкалы. Осветительный узел имеет поворотную обойму 7, со стеклянным светофильтром и матовым стеклом и п атрон с лампочкой, установка которого производится тремя винтами 9. Траверса крепится болтом к литому основанию 13, с вмонтированным внутрь его трансформатором, через который питается лампочка от сети переменного тока 220 В.
На передней части основания находится тумблер, снизу основания предохранитель, с тыльной стороны основания – вилка разъёма 11 для подключения электролампочки к трансформатору и винт заземления 12.
50
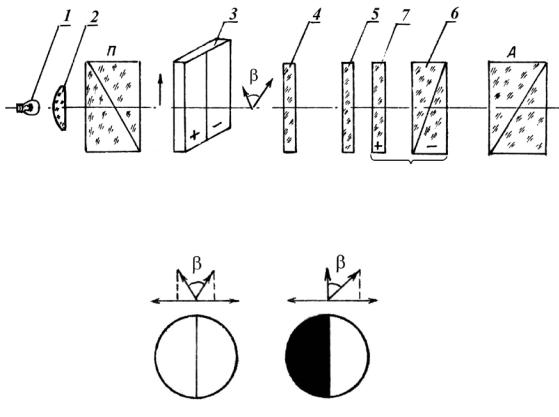
Принципиальная схема прибора приведена на рисунке 5.7.
компенсатор
Рисунок 5.7 – Принципиальная схема прибора
а) б)
а – равномерная освещенность, б – неравномерная освещенность
Рисунок 5.8 – Поле зрения окуляра
Анализатор А повёрнут относительно поляризатора П так, чтобы свет полностью гасился, то есть призмы Николя скрещены (см. закон Малюса – (5.1)). Световой поток от лампочки 1 проходит конденсорную линзу 2, попадает на поляризатор П и выходит из него плоскополяризованным. За поляризатором П стоит бикварцевая пластинка 3 и два защитных стекла 4 и 5, между которыми устанавливается трубка с исследуемым раствором. Кварцевый компенсатор, состоящий из подвижного клина 6 и неподвижной кварцевой пластинки 7, компенсирует вращение плоскости колебания, вызванное исследуемым раствором. За кварцевым ко мпенсатором установлен анализатор А, обнаруживающий поворот плоскости колебаний. Бикварцевая пластинка 3 состоит из двух склеенных пластин из лево- и правовращающего кварца, обозначенных соответственно "+" и " -". Усло-
вимся вектор E в плоскополяризованной волне обозначать стрелкой ↑ (см. рисунок 5.7). Плоскость колебаний светового вектора, вышедшего из поляризатора П поворачивается одной частью пластинки 3 в левую сторону, другой – в правую на такой же угол. Пластинка 7 изготовлена из правовращающего кварца. Пластинка 6, состоящая из двух левовра-
51
щающих клиньев кварца, соединена с кремальерной передачей. При вращении рукоятки 7, кремальерной передачи (см. рисунок 5.6) клинья 6 (см. рисунок 5.7) перемещаются друг относительно друга по вертикали, вследствие чего изменяется толщина пластинки 6 (см. рисунок 5.7).
При нормальном положении клиньев (нулевой отсчёт) компенсатор (6-7) не вращает плоскости колебаний, и без трубки обе половины поля зрения окуляра будут освещены одинаково (см. рисунок 5.8, а). Наличие трубки с оптически активным раствором вызовет поворот плоскости колебаний, и равномерная освещённость нарушится (см. рисунок 5.8, б). Для того чтобы получить равномерную освещённость поля зрения и применяется компенсационное устройство, состоящее из пластинок 6 и 7 (см. рисунок 5.7). При изменении толщины пластинки 6 можно повернуть плоскости колебаний так, чтобы обе половины поля зрения были освещены одинаково. Перемещение клиньев фиксируется по шкале. В
сахариметре применена международная сахарная шкала. 100° S этой шкалы соответствует 34,62 круговым градусам. За 100° S принят поворот плоскости колебаний при прохождении плоскополяризованного света через раствор толщиной 200 мм при температуре 20° С и приготовленный следующим образом: 26 г химически чистой сухой сахарозы растворяют в таком количестве дистиллированной воды, чтобы объём раствора был равен 100 см3. Пределы измерения сахариметра СУ – 2 от – 40° S до + 100° S. Знак «+» указывает правое, а «–» левое вращение плоскости колебаний.
5.4 Безопасность труда
Сахариметр включается в сеть переменного тока на 220 В 50 Гц через понижающий трансформатор. Запрещается работа с прибором без заземления.
5.5 Приборы и принадлежности
В работе используются: сахариметр универсальный типа СУ-2 или СУ-3 и набор поляриметрических трубок с растворами.
5.6 Порядок работы
5.6.1 Включить источник света.
5.6.2 Установить окуляр зрительной трубы 16 и отсчетную лупу 1 шкалы (см. рисунок 5.6) по глазу наблюдателя. Для этого, вращая оправы, передвинуть их вдоль оси так, чтобы в поле зрения окуляра зрительной трубы вертикальная линия, разделяющая поле зрения на две половины, была четко и ясно в идна, а в поле зрения отсчетной лупы четко и ясно были видны штрихи и цифры шкалы и нониуса.
5.6.3 Проверить нулевую точку прибора. Для этого, при отсутствии в камере трубки с раствором, добиться одинаковой освещенности обеих
52
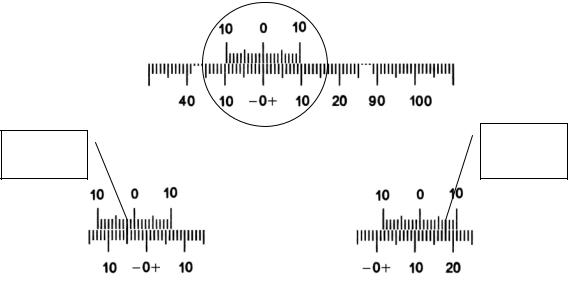
половинок поля зрения, вращая рукоятку кремальерной передачи 14. При
этом нулевые деления шкалы и нониуса должны |
совпадать, как |
показано на рисунке 5.9, а. |
|
Если этого нет, то с помощью ключа 4 (см. рисунок |
5.6) следует |
переместить нониус до совмещения его нулевого деления с нулевым делением шкалы. Отсчет показаний при помощи нониуса поясняется рисунками 5.9,б и 5.9,в. На рисунке 5.9,б показано положение шкалы и нониуса, соответствующее отсчету + 11,8 (нуль нониуса расположен правее нуля шкалы на 11 полных делений и в правой части нониуса с одним из деле-
ний |
шкалы совмещается 8-ое деление нониуса). На рисунке 5.9,в показа- |
но |
положение шкалы и нониуса, соответствующее отсчету –3,2 (нуль |
нониуса расположен левее нуля шкалы на 3 полных деления и в левой части нониуса 2-е деление нониуса совмещается с одним из делений шкалы).
5.6.4 По эталонным растворам сахара с известной концентрацией произвести градуировку прибора. Для этого необходимо в камеру поочередно вкладывать трубки с испытуемыми растворами. Вращая рукоятку кремальерной передачи, нужно добиться однородной освещенности обеих половинок поля зрения окуляра. После этого нужно произвести отсчет показаний с точностью до 0,1 деления шкалы при помощи нониуса. Данные занести в таблицу 5.1.
5.6.5 Построить градуировочный график зависимости концентрации от угла поворота С=С(ϕ) и по нему определить концентрацию 2-х растворов с неизвестным содержанием сахара.
нониус
|
шкала |
|
–3,2 |
+11,8 |
|
а) |
||
|
б) |
в) |
а– установка нулевой точки отсчета; б– отсчет равен –3.2; в– отсчет равен +11.8
Рисунок 5.9 – Примеры отсчета показаний при помощи нониуса
53
5.6.6 По данным таблицы рассчитать удельную постоянную вращения раствора сахара α в угл. град/(дм г см-3).
5.6.7 Определить абсолютную и относительную погрешности α.
5.6.8 Сделать выводы.
Таблица 5.1 – Результаты измерений и вычислений С=С(ϕ)
Номер |
|
|
Отсчеты |
ϕ , °S |
|
|
|
|
опыта |
|
|
|
|
|
|
|
|
С= |
С= |
|
С= |
С= |
С= |
С= |
С= |
|
|
|
|||||||
|
L= |
L= |
|
L= |
L= |
L= |
L= |
L= |
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
среднее |
|
|
|
|
|
|
|
|
значение ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.7 Контрольные вопросы
5.7.1 Что такое световая волна?
5.7.2 Какая волна называется плоскополяризованной?
5.7.3 Какая плоскость называется плоскостью колебаний, поляризации?
5.7.4 Понятие анизотропной среды.
5.7.5 В чем состоит явление двойного лучепреломления?
5.7.6 Устройство призмы Николя.
5.7.7 Какие вещества называются оптически активными?
5.7.8 Закон Малюса.
5.7.9 Что называется удельной постоянной вращения?
Литература
1 Савельев И. В.Курс общей физики / И. В. Савельев: в 3 т.– М.: Наука, 1978. – Т. 2.
2 Чечулин А. А. Волновые процессы. Оптика. Элементы атомной и ядерной физики / А. А. Чечулин – М.: Физматгиз, 1959.
3 Сахариметр универсальный типа СУ-3, 1965.
54
