1 Определение показателя преломления жидкостей и концентрации сахара в растворе при помощи рефрактометра

Относительный показатель преломления n21 при переходе луча света из среды с абсолютным показателем преломления n1 в среду с абсолютным показателем преломления n2 называется физическая величина, равная обратному отношению скоростей света в данных средах

Принцип обратимости световых лучей: если луч света направить обратно из среды с показателем преломления n2 в среду с показателем

преломления n1 , то ход падающего и преломленного лучей не изменится

(например, лучи 1′ и 1 на рисунке 1.1).

Если свет переходит из оптически менее плотной среды в оптически более плотную среду, как показано на рисунке 1.1, то угол преломления меньше угла падения.

Если свет от источника света S переходит из оптически более плотной среды с показателем преломления n1 в оптически менее плотную среду с

показателем преломления n2 , то угол преломления больше угла падения.

На рисунке 1.2 луч 1 падает на границу раздела двух сред под углом 0o и выходит во вторую среду не преломляясь. Лучи 2 и 3, падая на границу раздела двух сред под большими углами, претерпевают частичное преломление и отражение. При увеличении угла падения (луч 4) угол

Рисунок 1.2 – Ход лучей при переходе из оптически более плотной среды

в оптически менее плотную среду

преломления может достичь значения 90o. В этом случае преломленный луч скользит по границе раздела сред (луч 4′). Дальнейшее увеличение угла падения α приводит к тому, что световой луч не преломляется, а отражается от поверхности раздела внутрь оптически более плотной

среды, как луч 5′′ на рисунке 1.2.

Предельным углом полного внутреннего отражения называется угол падения αпр , для которого угол преломления β = 90o. Полным внутренним отражением называется явление, при котором происходит

6

отражение лучей от оптически менее плотной среды под углом α ≥ αпр. Формула (1.1) для полного внутреннего отражения имеет вид:

Таким образом, измеряя предельный угол полного внутреннего отражения по формуле (1.4) можно рассчитать показатель преломления среды.

1.2.2 Связь концентрации раствора с его абсолютным

показателем преломления

Согласно классической теории дисперсии света, при прохождении света через вещество происходят вынужденные колебания заряженных частиц (электронов и ионов) под действием электромагнитного поля световой волны [2]. При этом происходит поляризация молекул. Для изотропных газов и жидкостей поляризуемость p частицы определяется

Величина удельной рефракции, в отличие от абсолютного показателя преломления, не зависит от плотности вещества и является свойством только самой частицы. Связь удельной рефракции r вещества и с его абсолютным показателем преломления n описывается формулой Лоренц – Лорентца [2, 3]:

где ρ – плотность вещества.

Удельную рефракцию R смеси или химического соединения двух

где η1 и η2 – объемные доли первого и второго веществ в растворе.

7

Молярная концентрация вещества C – это количество вещества,

содержащегося в единице объема [4]. Объемная доля вещества η в растворе связана с молярной концентрацией С по формуле:

где µ – молярная масса вещества.

Решая систему уравнений, состоящую из формул (1.6) и ( 1.7), с учетом формулы (1.8), можно получить следующую зависимость концентрации растворенного вещества С от показателя преломления раствора n

где А и В – константы, определяемые по формулам:

A = n12 −1 1 ,

n12 + 2 ρ1

где n1, n2 – показатели преломления растворителя и растворенного вещества; ρ1, ρ2 – плотности растворителя и растворенного вещества; µ2

– молярная масса растворенного вещества.

Таким образом, измеряя показатель преломления раствора, можно рассчитать концентрацию вещества в растворе с помощью формулы (1.9).

1.4Экспериментальная часть

1.4.1Безопасность труда

Вработе используется рефрактометр лабораторный РЛ–2, подключаемый к сети переменного тока 220 В. Перед включением в сеть убедитесь в исправности сетевого шнура.

Жидкости и растворы, используемые в работе, являются химическими реактивами, которые категорически запрещается пробовать и нюхать.

1.4.2Приборы и принадлежности

В лабораторной работе используется рефрактометр лабораторный РЛ–2, пипетка, салфетка, набор жидкостей для определения показателя преломления и набор растворов для определения концентрации сахара.

8

дисперсионный лимб с рукояткой 12, соединенный с оправой призмы прямого зрения, при помощи которой устраняется спектральная окраска границы светотени. Граница светотени становится резкой.

1.4.2.2 Методика измерений, основанная на законе полного

внутреннего отражения

Основной частью рефрактометра являются две призмы АВС и А′В′С′, изготовленные из флинтгласа с большим показателем преломления n =1,72 . Между призмами вводят три капли исследуемой жидкости,

которая расплывается в слой толщиной 0,02 мм при опускании верхней призмы на нижнюю.

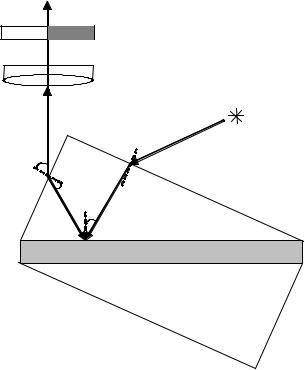
Ход лучей в рефрактометре при использовании метода полного внутреннего отражения показан на рисунке 1.4. При этом призму АВС освещают со стороны матовой грани ВС через окошко 7 (см. рисунок 1.3). Свет в этом случае падает на границу раздела АВ под всевозможными углами. Каждому падающему лучу соответствует предельный угол преломления r1′. При r1 > r1′ наступает полное внутреннее отражение, при

r1 < r1′ свет отражается лишь частично. В связи с этим угол выхода луча i из грани АС может изменяться лишь в интервале от некоторого значения до

90o .

B′

Рисунок 1.4 – Ход лучей в рефрактометре при использовании метода

полного внутреннего отражения

10

В поле зрения трубы Т, поставленной на пути лучей, прошедших систему двух призм, наблюдаются светлая и темная области. Положение границы светотени определяется величиной предельного угла i, то есть зависит от величины показателя преломления n жидкости.

1.5 Порядок выполнения работы

1.5.1 Подготовка к работе

1.5.1.1Подключить сетевые шнуры рефрактометра.

1.5.1.2Проверить нуль-пункт прибора. Для этого поднять осветительную призму верхней камеры 5 (см. рисунок 1.3) и на поверхность нижней камеры 4 пипеткой нанести 2-3 капли дистиллированной воды.

1.5.1.3Опустить верхнюю призму и, пользуясь осветителем, направить пучок света через окно на верхнюю призму.

1.5.1.4Установить окуляр 11 на резкость по шкале и визирной линии

сетки, представляющей собой три штриха. После этого переместить окуляр при помощи рукоятки 10 по шкале до тех пор, пока в изирная линия не совместится с границей светотени.

1.5.1.5При правильной установке прибора на нуль-пункт граница светотени при 20 °С должна быть совмещена с делением шкалы показателей преломления n, равным 1,333.

1.5.2Определение показателей преломления жидкостей

1.5.2.1Поднять верхнюю призму и на поверхность нижней призмы пипеткой нанести 2-3 капли исследуемой жидкости. При этом не следует касаться пипеткой поверхности призмы, чтобы не поцарапать последнюю.

1.5.2.2Опустить верхнюю призму. При помощи окуляра и рукоятки дисперсионного лимба 12 (см. рисунок 1.3) устранить окрашенность поля

идобиться резкой границы светотени.

1.5.2.3Рукояткой 10 совместить границу светотени с визирной линией. Снять показания с прибора. Данные занести в таблицу 1.1.

1.5.2.4Повторить 1.5.2.1– 1.5.2.3 пять раз.

Таблица 1.1 – Показатели преломления жидкостей

11

1.5.2.5 После работы с данной жидкостью тщательно промыть дистиллированной водой плоскости соприкосновения призм, протереть их насухо салфеткой.

1.5.2.8 Измерить показатели преломления нескольких исследуемых жидкостей, выполняя 1.5.2.1– 1.5.2.5. Данные занести в таблицу 1.1.

1.5.2.9. По справочным значениям показателей преломления определить жидкость. Данные занести в таблицу 1.1.

1.5.3 Определение концентраций сахара в растворах

1.5.3.1Выполняя 1.5.2.1– 1.5.2.5 с растворами сахара и проводя измерения с помощью правой шкалы рефрактометра, определить концентрации. Результаты измерений занести в таблицу 1.2.

1.5.3.2После окончания работы протереть насухо внутренние поверхности камер мягкой салфеткой. Накрыть прибор чехлом.

Таблица 1.2 – Концентрация сахара в растворе

1.5.4 Оценить погрешности измерений показателя преломления одной из жидкостей и концентрации одного из растворов.

1.5.5 Сделать вывод по работе.

1.6 Контрольные вопросы

1.6.1Что называется абсолютным и относительным показателями преломления?

1.6.2Что называется предельным углом полного внутреннего отраже-

ния?

1.6.3 В чем заключается явление полного внутреннего отражения? 1.6.4 Сформулируйте принцип обратимости световых лучей. 1.6.5 Назовите характеристики рефракции.

1.6.6 Что происходит с веществом при прохождении света через него?

1.6.7Что называется молярной концентрацией вещества в растворе?

1.6.8Принцип действия рефрактометра.

1.6.9 Ход лучей в рефрактометре при использовании метода полного внутреннего отражения.

12

Литература

1.Савельев И.В. Курс общей физики / И.В. Савельев: учебное пособие для вузов: в 4 кн. − 4-е изд., перераб. − М.: Наука. Физматлит, 1998.

Кн. 4: Волны. Оптика − 265 с.

2.Сивухин Д.В.Общий курс физики / Д.В. Сивухин: учебное пособие

для вузов: в 4 кн.– 3-е изд., стереот. − М.: Наука. Физматлит, 2005. Т.4: Оптика −792 с.

3.Ландсберг Г.С. Оптика / Г.С. Ландсберг – М.:Госиздат, 1957.– 552 с.

4.Сивухин Д.В.Общий курс физики / Д.В. Сивухин: учебное пособие

для вузов: в 4 кн.– 3-е изд., испр. и доп. − М.: Наука. Физматлит, 1990. Т.2: Термодинамика и молекулярная физика −591 с.

5.Рефрактометр лабораторный РЛ-2: Описание и правила пользования рефрактометром лабораторным типа РЛ - 2. – Киев: Госсельхозиздат, 1963.

–14 с.

6.Лабораторные занятия по физике / Под редакцией Л.Л. Гольдина. − М.: Наука. Физматлит, 1983. − 688 с.

13

2 Определение длины световой волны с помощью колец Ньютона

2.1 Цель работы

Целью работы является изучение явлений интерференции света, определение длины световой волны по интерференционной картине с помощью колец Ньютона.

2.2Теоретическое введение

2.2.1 Интерференция света

Интерференцией света называется пространственное перераспределение светового потока при наложении двух или нескольких когерентных волн, в результате которого в одних местах возникают максимумы, а в других минимумы интенсивности [1].

Когерентностью называется согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов [1]. Когерентными волнами называются волны одинаковой частоты, разность фаз которых остается постоянной во времени. Условию когерентности удовлетворяют монохроматические волны, то есть неограниченные в пространстве волны одной определенной и строго постоянной частоты.

В большинстве источников света волны немонохроматичны. Это обусловлено механизмом испускания световых волн. Атомы испускают световые волны при переходе из возбужденного состояния в основное (в более общем случае – из состояния с большей энергией в состояние с меньшей энергией). Процесс излучения длится около 10-8с. Частота испускаемой волны определяется разницей между соответствующими энергетическими уровнями:

энергия атома в возбужденном состоянии; E1 – энергия атома в основном

состоянии.

Возбудившись вновь, атом испустит световую волну, но уже с другой начальной фазой и возможно другой частотой. Прерывистое излучение света атомами в виде отдельных коротких импульсов называется волновым цугом. Когерентность может существовать только в пределах одного цуга. Любой немонохроматический свет можно представить как совокупность сменяющих друг друга независимых цугов. Средняя про-

должительность одного цуга τког называется временем когерентности. Расстояние, на которое волна распространится в вакууме за время когерентности, lког = cτког , называется длиной когерентности (или длиной

14

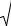
цуга). Наблюдение интерференции световых волн возможно только при оптических разностях хода, меньших длины когерентности.

Рассмотрим интерференцию монохроматических волн от двух когерентных источников S1 и S2. Плоские монохроматические волны описываются уравнением:

координатой x = 0 ).

Применительно к электромагнитным волнам уравнение (2.2) пере-

Уравнение (2.3) описывает колебание электрического поля, уравнение (2.4) описывает колебание магнитного поля.

Предположим, что в некой точке пространства источниками S1 и S2 возбуждаются колебания одинакового направления:

колебания.

Под x понимается напряженность электрического или магнитного полей волны. Напряженность электрического и магнитного полей подчиняется принципу суперпозиции. Амплитуда результирующего колебания в данной точке определяется выражением:

Интенсивность световой волны пропорциональна квадрату амплитуды и определяется выражением:

Если волны не когерентны, то разность фаз, ϕ2 −ϕ1 , постоянно

меняется и в среднем по времени равняется нулю. В этом случае результирующая интенсивность в данной точке пространства определяется арифметическим сложением интенсивностей падающих волн. Для

когерентных волн разность фаз, ϕ2 −ϕ1 , в данной точке пространства имеет постоянное во времени значение. В случае, когда cos(ϕ2 −ϕ1 )> 0 ,

интенсивность I > I1 + I2 . Если cos(ϕ2 −ϕ1 )< 0 , интенсивность I < I1 + I2 .

То есть имеет место интерференция света.

Рассмотрим, чем определяется разность фаз складываемых колебаний. Пусть разделение на две волны происходит в точке 0. До точки M, в

15

которой наблюдается интерференционная картина, одна волна прошла путь s1 в среде с показателем преломления n1, другая волна прошла путь s2 в среде с показателем преломления n2. Если в точке 0 фаза колебаний равна ω t , то в точке M первая волна придет с фазой:

где t1 ( t2 ) – время движения волнового фронта от точки 0 до точки M по

соответствующему пути. Или, выражая t1 и t2 через пройденный путь и фазовую скорость, фазы 1-й и 2-й волн в точке М перепишутся в виде:

С учетом того, что фазовая скорость волны определяется отношением скорости света к показателю преломления среды (υ = nc ), выражения для значений фаз в точке М можно переписать как:

Это условие будет выполняться, когда оптическая разность хода равняется целому числу длин волн в вакууме:

Колебания, возбуждаемые в точке М, будут происходить в противофазе, когда:

16

Уравнение (2.19) является условием интерференционного минимума.

2.2.2 Изучение интерференции методом колец Ньютона

Кольца Ньютона наблюдаются при отражении света от воздушного зазора, образованного плоскопараллельной прозрачной пластинкой и соприкасающейся с ней плосковыпуклой линзой с большим радиусом кривизны. Принципиальная схема установки для получения колец Ньютона приведена на рисунке 2.1.

4

Рисунок 2.1 – Принципиальная схема установки для получения колец Ньютона

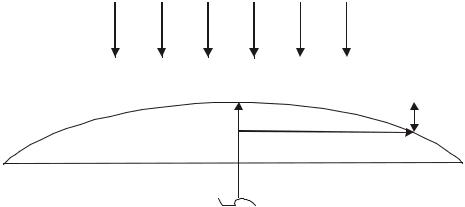
Если на линзу падает пучок монохроматического света, то световые волны, отраженные от верхних и нижних границ воздушного зазора, будут интерферировать между собой. Интерференционная картина представляет собой полосы равной толщины, центры которых лежат на оси симметрии линзы, согласно рисунку 2.2. При нормальном падении лучей, полосы имеют вид концентрических окружностей. Кольца Ньютона могут наблюдаться как в проходящем, так и в отраженном свете.

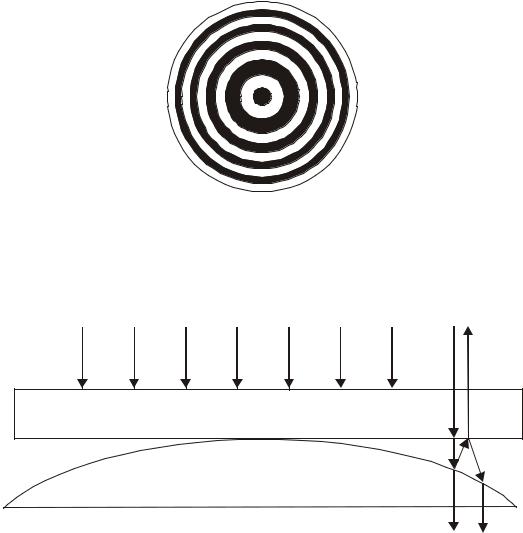
Проведем расчет размеров колец Ньютона в проходящем свете при нормальном падении светового потока. Ход лучей при получении колец Ньютона приведен на рисунке 2.3. Световой луч, прошедший через воздушную прослойку, частично преломляется (луч АД) и частично отражается (луч АВ). Отраженный луч, в свою очередь, вновь разделяется на преломленный (БЕ) и отраженный (БВ). Если радиус кривизны линзы R

17

достаточно велик и соответственно толщина воздушной прослойки d

Рисунок 2.2 – Кольца Ньютона

Рисунок 2.3 – Ход лучей при получении колец Ньютона

достаточно мала, то лучи ОА и БВ практически накладываются друг на друга и наблюдается интерференционная картина. Так как преломление на выпуклой грани мало, оптическую разность хода между лучами ОА и БВ можно полагать равной 2·n·d. С учетом того, что показатель п реломления воздуха равен единице, оптическая разность хода равняется 2·d. При отражении света от оптически более плотной среды фаза колебаний вектора напряженности электрического поля изменяется на π . Луч ОА – АБ – БВ испытывает двукратное отражение от оптически более плотной среды. В связи с этим между лучами ОА и БВ во зникает дополнительная разность фаз 2π . В точках, для которых выполняется условие (2.17), возникают максимумы, в точках для которых выполняется условие (2.18), – минимумы интенсивности.

18

Оба условия можно объединить в одно:

где четным m соответствуют максимумы, нечетным – минимумы интенсивности. Величину dm можно вычислить из геометрических соображений:

где R – радиус кривизны линзы; rm – радиус темного или светлого кольца, соответствующего целому числу m. Отсюда:

Из уравнения (2.22) следует выражение для радиуса m-го темного или светлого кольца:

r = mR λ , (m=0,1,2, …). (2.23)

На основе формулы (2.23) можно определить длину волны света. Запишем радиусы p-го и n-го колец:

В лабораторной работе используется микроскоп МИР-12 [2], внешний вид которого приведён на рисунке 2.4. Микроскоп позволяет получить картину колец Ньютона в проходящем свете. Фокусировка изображения осуществляется вращением объектива 10. После получения сфокусированного изображения, объектив закрепляется контргайкой 11. В промежутках между измерениями проводить перефокусировку нельзя. Отсчетный барабан 12 обеспечивает перемещение микроскопа в горизонтальном направлении в пределах от 0 до 50 мм. Целые миллиметры

19

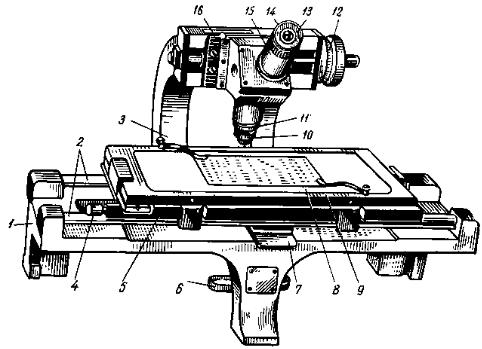
отсчитываются по миллиметровой шкале 16. Десятые и сотые доли миллиметра – по барабану 12. Цена деления барабана 0,01 мм. Десятые доли барабана (микроны) оцениваются на глаз.

1 – литая станина; 2 – цилиндрические направляющие продольного перемещения столика;

3 – кронштейн; 4 – винт углового поворота столика; 5 – столик для спектрограмм с матовым стеклом 8; 6 – осветительное зеркало; 7 – пружинная рукоятка; 9 – рамка для поперечного перемещения столика; 10 – объектив; 11 – контргайка для закрепления объектива; 12 – отсчетный барабан; 13 – оправа глазной линзы; 14 – зажимной хомутик; 15 – цилиндрическая оправа окуляра; 16 – миллиметровая шкала

Рисунок 2.4 – Измерительный микроскоп МИР-12

2.4Безопасность труда

В качестве источника света в приборе используется ртутная лампа. Излучение ртутной лампы может представлять опасность для зрения. В связи с этим на ртутную лампу надо смотреть только через светофильтр. Также запрещается работа с прибором без заземления.

2.5Приборы и принадлежности

Вработе используются микроскоп МИР-12, ртутная лампа, светофильтры, световод, установка для наблюдения колец Ньютона.

20

2.6 Порядок работы

2.6.1 Установить осветитель со светофильтром (с известной длиной волны) перед микроскопом.

2.6.2 Направить с помощью световода луч света от осветителя на зеркало микроскопа таким образом, чтобы луч падал нормально на плоскопараллельную пластинку.

2.6.3 Вращением объектива 5 получить резкое изображение колец Ньютона.

2.6.4 Измерить диаметры семи темных колец, начиная со второго. Для измерения диаметра кольца нужно совместить с помощью винта 7 штрих окуляра с серединой левой части кольца и снять полученное значение – x1. Далее повторить ту же операцию с правой частью кольца и получить значение x2. Диаметр кольца находится как модуль разности полученных

значений d = x2 − x1 .

2.6.5 Повторить измерение диаметра каждого кольца по три раза и определить среднее значение.

2.6.6 Результаты измерений занести в таблицу 2.1.

Таблица 2.1 – Результаты измерений диаметров колец Ньютона В миллиметрах

2.6.7 На основе проведенных измерений рассчитать с помощью формулы (2.25) радиус кривизны линзы R, подставляя в нее диаметры несоседних колец (получить не менее пяти значений R, по результатам которых рассчитывается среднее). Результат занести в таблицу 2.2.

Таблица 2.2 – Результаты расчета радиуса кривизны линзы

21

2.6.8 Установить светофильтр, пропускающий свет с неизвестной длиной волны.

2.6.9 Измерить диаметры семи колец Ньютона (начиная со второго) для излучения с неизвестной длиной волны в соответствии с 2.6.3 – 2.6.5. Результаты измерений занести в таблицу 2.3, аналогичную таблице 2.1.

2.6.10 Используя данные таблицы 2.3 и найденный радиус кривизны линзы R, рассчитать с помощью формулы (2.25) неизвестную длину волны, подставляя в формулу диаметры несоседних колец (получить не менее пяти значений λ, по результатам которых рассчитать среднее).

2.6.11 Вычислить погрешность измерения длины волны ∆λ. Записать

результат в виде λ=<λ> ± ∆λ. 2.6.12 Сделать выводы.

2.7 Контрольные вопросы

2.7.1 Что такое интерференция?

2.7.2 Что такое когерентность? Какие волны называются когерентными?

2.7.3 Что такое волновой цуг?

2.7.4 Записать уравнение плоской монохроматической волны.

2.7.5 Записать условие интерференционного максимума и минимума.

2.7.6 Записать формулу для результирующей интенсивности при наложении двух когерентных волн.

2.7.7 Показать ход лучей для получения колец Ньютона в проходящем свете.

2.7.8 Дать понятие полос равной толщины.

2.7.9 Пояснить расчетную формулу для определения длины волны.

Литература

1 Савельев И. В. Курс общей физики. /И.В. Савельев: учебное пособие: в 3 т. – 3-е изд., перераб. – М.: Наука, 1988. – Т 2: Электричество и магнетизм. Волны. Оптика. – 496 с.

2 Барсуков В.И. Атомный спектральный анализ / В.И. Барсуков – М.: «Издательство Машиностроение-1», 2005. – 132 с.

22