
- •Содержание
- •1. Введение
- •1.3. Три закона деформирования сплошного твёрдого тела
- •2. Закон равновесия. Теория напряжений
- •2.1. Напряженное состояние в точке
- •2.2. Дифференциальные уравнения равновесия элемента сплошного твердого тела
- •2.3. Граничные условия в напряжениях
- •2.4. Анализ напряженного состояния в точке
- •2.4.2. Исследование нормальных напряжений
- •2.4.3. Исследование касательных напряжений
- •2.4.4. Поверхности напряжений
- •2.4.5. Графическое исследование напряжений. Круги Мора
- •3. Закон сплошности. Теория деформаций
- •3.2. Исследование деформированного состояния в точке
- •4. Физический закон. Обобщенный закон Гука
- •4.3. Основные упругие постоянные
- •5. Уравнения и задачи упругого равновесия
- •5.1. Основные граничные задачи теории упругости
- •5.2. Уравнения теории упругости в перемещениях
- •5.3. Уравнения теории упругости в напряжениях
- •5.6. Общее решение уравнений теории упругости
- •5.7. Пропорциональность перемещений, напряжений и деформаций действующей нагрузке
- •6. Постановка температурных задач линейной теории упругости
- •7. Постановка динамических задач линейной теории упругости
- •8. Криволинейные координаты
- •8.1. Уравнения линейной теории упругости
- •- граничные условия в напряжениях
- •8.2. Уравнения линейной теории упругости в сферических координатах
- •Из граничных условий в напряжениях на боковой поверхности вала остается только одно уравнение:
- •Под плоской задачей теории упругости понимают совокупность двух родственных в математическом отношении задач:
- •Список литературы
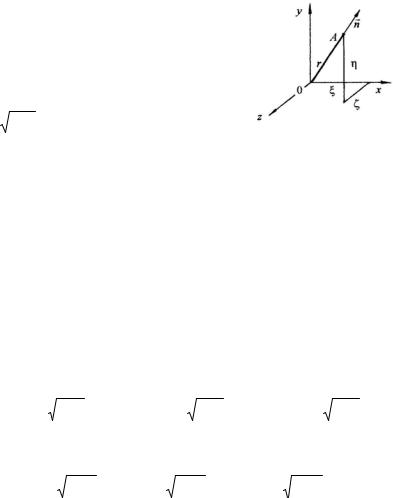
2.4.4. Поверхности напряжений
Вопрос о существовании главных площадок, главных напряжений, главных осей тензора напряжений и т.д. может быть решен с помощью так называемых поверхностей напряжений.
Рассмотрим площадку с нормалью nr , направление которой определяется направляющими косинусами l , m , n . Нормальное напряжение на этой площадке равно σn . Отложим на направлении нормали
отрезок, |
|
|
величина |
которого |
равна |
||
r =1/ |
|
|
σn |
|
(рис. 2.8). |
|
Рис. 2.8 |
|
|
|
|||||
|
|
|
|
|
|
|
|
Будем давать нормали все возможные направления (т.е. рассматривать все возможные площадки, проходящие через данную точку) и откладывать на этих нормалях соответствующие значения r . Очевидно, что конец отрезка r опишет какую-то поверхность. Получим уравнение этой поверхности.
Величина нормального напряжения определяется известной формулой:
σn = σxl 2 + σy m2 + σz n2 + 2τxyl m + 2τyz m n + 2τzx n l .
Проекции отрезка r |
обозначим через |
ξ, |
η и ζ (одновременно |
|||||||||||||||||||||||
можно считать что |
ξ, |
η и ζ − координаты конца отрезка r ). Оче- |
||||||||||||||||||||||||
видно, что эти проекции (или координаты конца отрезка) равны: |
||||||||||||||||||||||||||
ξ = r l = l / |
|
σn |
|
|
, |
η = r m = m / |
|
|
|
|
σn |
|
, |
ζ = r n = n / |
|
σn |
|
, |
||||||||
|
|
|
|
|
|
|||||||||||||||||||||
откуда следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
l = ξ |
|
σn |
|
, m = η |
|
σn |
|
|
, |
n = ζ |
|
σn |
|
. |
||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
Подставляем значения |
l , m , n |
в формулу для напряжения σn . |
||||||||||||||||||||||||
Будем иметь: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
35
σxξ2 + σy η2 + σz ζ2 + 2τxy ξ η + 2τyz ηζ + 2τzxζξ = ±1 .
Известно, что всякое уравнение второго порядка может быть приведено к каноническому виду, когда члены с произведениями координат отсутствуют. Координатные оси, в которых уравнение второго порядка имеют канонический вид, носят название главных осей. Для того чтобы полученное уравнение могло быть приведено к каноническому виду, необходимо, чтобы на площадках, нормалями к которым служат главные оси, касательные напряжения (как коэффициенты уравнения) были равны нулю. Этим самым утверждается, что в каждой точке тела есть три главные площадки с главными нормальными напряжениями.
Полученное уравнение определяет поверхность второго порядка, которая носит название поверхности напряжений Коши.
С помощью представления о поверхностях напряжений легко доказать одно из утверждений, которыми мы уже пользовались, а именно то, что значения главных напряжений σ1 , σ2 , σ3 в общем
случае различны.
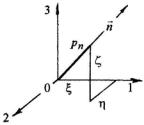
Проведем через данную точку тела три главные оси и рассмотрим площадку с нормалью n .
Направление нормали, как обычно, задаем направляющими косинусами l , m , n . Проекции полного напряжения p n как
отрезка, отложенного по направлению нормали из начала координат, на главные оси (рис. 2.9), будут равны:
Рис. 2.9 |
ξ = σ1l , |
η = σ2 m , ζ = σ3 n . |
Отсюда имеем: |
|
|
l = ξ/ σ1 , |
m = η/ σ2 , |
n = ζ / σ3 . |
Поскольку направляющие косинусы связаны между собой соот-
ношением l 2 + m2 + n2 =1, уравнение поверхности напряжений будет иметь вид:
36
ξ2 |
|
η2 |
|
ζ2 |
|
|
+ |
σ2 |
+ |
|
=1 . |
σ2 |
σ2 |
||||
1 |
|
2 |
|
3 |
|
Полученное уравнение есть уравнение эллипсоида, который носит название эллипсоида Ламе ( σ1 , σ2 , σ3 – полуоси эллипсоида).
Уравнение показывает, что в общем случае одно из главных напряжений имеет наибольшее значение, другое – наименьшее, а третье – промежуточное.
2.4.5. Графическое исследование напряжений. Круги Мора
Примем, что координатные оси совпадают с главными осями напряженного состояния. Для нормального напряжения σn на
произвольной площадке имеем
σ |
n |
= σ l 2 |
+ σ |
2 |
m2 + σ |
3 |
n2 . |
|
1 |
|
|
|
Полное напряжение на этой же площадке мы можем записать, используя формулу
σ2n + τn2 = (σ1 l)2 + (σ2 m)2 + (σ3n)2 .
Направляющие косинусы нормали к рассматриваемой площадке связаны соотношением
1 =l 2 + m 2 + n 2 .
Полученные три уравнения можно рассматривать как систему уравнений, определяющих направляющие косинусы l , m , n для произвольной площадки. Решим полученную систему уравнений относительно этих неизвестных. Определим вначале направляющий косинус l , а для этого проведем следующие операции:
- умножим выражение для σn на сумму (σ2 +σ3 );
- полученное соотношение вычтем из уравнения для полного напряжения;
37
- к полученному результату прибавим третье уравнение, умноженное на σ2σ3 .
Выполнение перечисленных операций позволяет получить следующее уравнение относительно направляющего косинуса l :
σn2 + τ2n − σn (σ2 + σ3 )+ σ2σ3 = (σ1l)2 + (σ2 m)2 + (σ3n)2 −
− (σ |
2 |
+ σ |
3 |
)(σ l 2 |
+ σ |
2 |
m2 + σ |
3 |
n2 ) + σ |
2 |
σ |
3 |
(l 2 |
+ m2 + n2 ) . |
|
|
1 |
|
|
|
|
|
|
Действительно, после некоторых преобразований будем иметь:
τ2 |
+(σ |
n |
−σ |
2 |
)(σ |
n |
−σ |
3 |
)= l2 (σ −σ |
2 |
)(σ −σ |
3 |
) |
, |
n |
|
|
|
|
1 |
1 |
|
|
откуда следует, что
l |
2 |
= |
τn2 + (σn − σ2 )(σn − σ3 ) |
. |
|||||
|
(σ − σ |
3 |
)(σ − σ |
2 |
) |
|
|||
|
|
|
1 |
1 |
|
|
|
||
Аналогичным образом из начальной системы уравнений определяем соотношения для направляющих косинусов m2 и n2 :
|
2 |
|
|
τ2 |
+ (σ |
n |
− σ |
3 |
)(σ |
n |
|
− σ |
1 |
) |
|
||||||||||||||||
m |
= |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|||||||
|
|
|
|
(σ |
2 |
|
− σ |
3 |
)(σ |
2 |
|
− σ |
|
) |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||
|
2 |
|
τ2 |
|
+ (σ |
n |
− σ |
|
)(σ |
n |
− σ |
2 |
) |
|
|||||||||||||||||
n |
= |
|
n |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
. |
||||||||
|
|
|
(σ |
3 |
− σ |
|
)(σ |
3 |
− σ |
2 |
) |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Направляющие косинусы |
|
l , |
m , |
|
n будут иметь действительные |
||||||||||||||||||||||||||
значения, если правые части полученных соотношений будут положительными.
Примем, что σ1 > σ2 > σ3 . В этом случае σ1 −σ2 > 0 , σ1 −σ3 > 0.
Следовательно, чтобы значение l2 было положительным, нужно чтобы выполнялось условие
38
τn2 +(σn −σ2 )(σn −σ3 )≥ 0 .
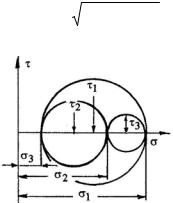
Если принять σn за абсциссу, a τn − за ординату, то в системе координат « σ − τ » уравнение
τ2 + (σ − σ2 )(σ −σ3 )= 0
определяет окружность. Действительно, уравнение x2 + y2 + 2mx +
+ 2ny + q = 0 определяет окружность радиусом R = m2 + n2 − q с координатами центра x0 = −m и y0 = −n .
В нашем случае R = (σ2 −σ3 )/ 2 , σ0 = (σ2 + σ3 )/ 2 и τ0 = 0 , т.е. центр окружности лежит на оси абсцисс, а сама окружность проходит через следующие две точки этой оси
(рис. 2.10):
τ = 0 |
, |
σ = σ2 |
; |
|
τ = 0 |
, |
σ = σ3 |
. |
Рис. 2.10 |
Рассматриваемое условие τ2n + (σn −σ2 )(σn −σ3 )≥ 0 определяет точки плоскости (σ, τ), лежащие на этой окружности и вне нее.
Поскольку σ2 −σ1 < 0, σ2 −σ3 > 0, для того, чтобы значение m2 было положительным, необходимо выполнить требование
τ2 |
+ (σ |
n |
−σ |
3 |
)(σ |
n |
− σ )≤ 0 . |
n |
|
|
|
1 |
Получаем новую окружность с центром на оси абсцисс, проходящую через точки σ1 и σ3 , лежащие на этой оси. Условие поло-
жительности m2 определяет, что точки плоскости (σ, τ) лежат внутри этой окружности или на ней.
Наконец, для положительности значения n2 необходимо, чтобы
39
τ2 |
+ (σ |
n |
− σ |
)(σ |
n |
− σ |
2 |
)≥ 0 . |
n |
|
1 |
|
|
|
Здесь имеем новую окружность, проходящую через точки σ1 и σ2 , лежащие на оси абсцисс. Условие положительности величины
n2 утверждает, что точки плоскости (σ, τ) должны лежать вне этой окружности или на ней.
Таким образом, для произвольной площадки, пересекающей все три главные оси, напряженное состояние представляется точкой, лежащей в области, ограниченной тремя окружностями (кругами Мора). Круговая диаграмма Мора подтверждает, что главных напряжений действительно может быть только три, и что величины экстремальных значений касательных напряжений действительно определяются полуразностями соответствующих главных напряжений.
Задачи
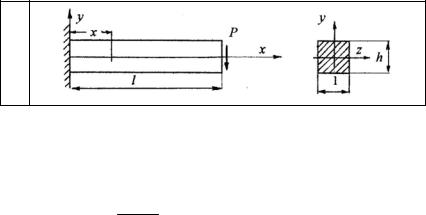
2.1.
Брус прямоугольного поперечного сечения, жестко закрепленный с левой стороны, изгибается в плоскости xoy силой P , представленной в
виде поверхностных сил, распределенных по торцу. Решение для напряжений, полученное в сопротивлении материалов, имеет вид:
σx = P (l − x)
J z
σy
|
|
P |
|
|
|
2 |
|
2 |
|
|
y , |
τxy = − |
|
h |
|
− y |
|
, |
|||
2J |
|
|
4 |
|
|
|||||
|
|
|
z |
|
|
|
|
|
|
|
= σz = τyz = τzx = 0 .
Проверить, удовлетворяются ли дифференциальные уравнения равновесия и граничные условия. По какому закону должны быть распределены поверхностные силы на торце бруса, чтобы удовлетворялись граничные условия?
40
Подстановка имеющихся соотношений для компонентов напряжений в дифференциальные уравнения равновесия показывает, что эти уравнения удовлетворяются тождественно.
Граничные условия должны быть проверены для верхней ( y = h / 2 ) и нижней ( y = −h / 2 ) граней и правого торца x = l .
На верхней грани поверхностные силы отсутствуют, т.е. X =Y = Z = 0 , а направляющие косинусы нормали к площадке, расположенной на этой грани, имеют значения: l = 0 , m =1 , n = 0 . Подставим соотношения для напряжений, поверхностных сил и направляющих косинусов в первое граничное условие:
|
|
|
|
|
|
|
|
2 |
|
|
|
X = σxl + τxym + τxzn |
0 = − |
P |
|
h |
|
− y |
2 |
≡ 0 , |
|||
2J |
|
|
4 |
|
|||||||
|
|
|
|
|
z |
|
|
|
|
y=h / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
т.е. рассматриваемое граничное условие удовлетворяется. К аналогичному выводу приходим, проверяя оставшиеся два граничных условия.
Легко видеть, что и для нижней грани граничные условия удовлетворяются. На торце бруса поверхностные силы представлены только неизвестным рас-
пределением силы P ( Y − ? , X = Z = 0 ). Направляющие косинусы нормали к площадке, расположенной на торце, имеют следующие значения: l =1, m = 0 , n = 0 . Соответственно, первые два уравнения граничных условий принимают вид:
|
|
|
|
|
|
|
P (l − x) |
|
|
|
|
|
|
, |
|
|
||||
|
|
|
|
0 = |
y |
|
|
≡ 0 |
|
|
|
|
||||||||
|
|
|
|
|
J z |
x=l |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
P |
|
|
h |
|
|
|
|
|
|
|
P |
|
|
h |
|
||
|
|
|
|
|
|
|
− y2 |
|
|
|
= − |
|
|
|
|
− y2 . |
||||
Y |
= − |
|
|
|
|
|||||||||||||||
2J |
|
4 |
|
|
|
|
2J |
|
4 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
z |
|
|
|
|
|
x=l |
|
|
|
z |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Третье граничное условие удовлетворяется.
Соотношение, полученное для Y , определяет закон распределения силы P на торце, при котором граничное условие на торце удовлетворяется.
2.2.
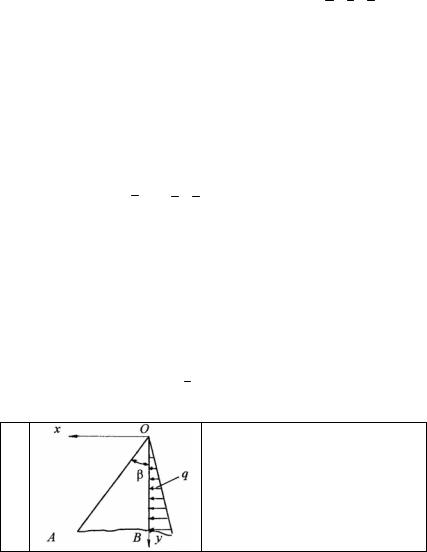
Записать граничные условия для линий OA и OB тела треугольной формы единичной толщины, к которому по линии OB приложена нагрузка q = γy .
41
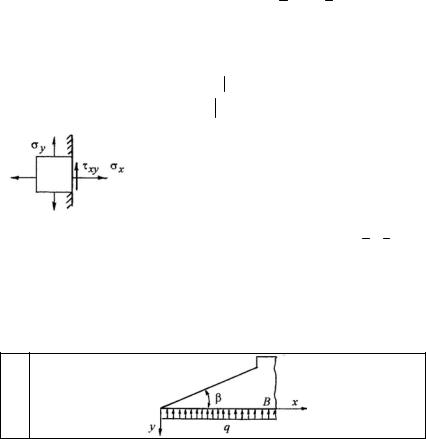
На линии (границе тела) OB ( x = 0 ) имеем, что X = γy , Y = 0 , а направляю-
щие косинусы нормали к площадке, расположенной на этой линии, принимают следующие значения: l = −1 , m = 0 . Подставляя соотношения для поверхностных
сил и направляющих косинусов в граничные условия, получим:
γy = −σx x=0 , 0 = τxy x=0 .
|
Эти же соотношения легко получить, исходя из |
|
физического смысла граничных условий. |
|
Действительно, рассмотрение элемента тела, выхо- |
|
дящего своей гранью на границу OB (рис. 2.11), пока- |
|
зывает, что соответствие между внутренними и внеш- |
|
ними силами на этой линии реализуется соотноше- |
Рис. 2.11 |
ниями, приведенными выше. |
На линии (границе тела) OA ( x = ytgβ) нагрузка отсутствует ( X =Y = 0 ), а направляющие косинусы определяются соотношениями l = cosβ , m = −sinβ . Соответственно, граничные условия будут иметь вид:
0 = σx cosβ−τxy sinβ , 0 = τxy cosβ−σy sinβ .
2.3.
В консольном выступе фундамента, имеющем треугольную форму и находящемся под действием равномерного давления грунта q , определе-
ны напряжения:
σx = A −
σy = A −
|
|
y |
|
|
|
|
|
|
xy |
|
|
|
|
|
arctg |
|
|
− |
|
|
|
|
|
|
|
+C |
, |
||
|
|
|
|
2 |
|
2 |
||||||||
|
|
x |
|
x |
+ y |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
y |
|
|
|
|
|
xy |
|
|
|
|
|
|
arctg |
+ |
|
|
|
|
|
|
|
+ B |
, |
||||
|
|
|
|
2 |
|
|
2 |
|
||||||
|
|
x |
|
x |
+ y |
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||
τxy = −A |
|
y2 |
, |
|
x2 |
+ y2 |
|||
|
|
σz = τyz = τzx = 0 .
Определить постоянные А, В, С из граничных условий.
42
Запишем граничные условия для линий OA и OB : |
|
||||||||||
- линия OA ( y = −xtgβ ) : |
|
|
|
|
|
= 0 ; |
l = −sinβ , |
m = −cosβ, |
|||
X |
=Y |
||||||||||
|
σx sinβ+ τxy cosβ = 0 |
, |
(1) |
||||||||
|
τxy sinβ+σy cosβ = 0 |
; |
(2) |
||||||||
- линия OB ( y = 0 ) : |
|
|
|
= −q ; |
l = 0 , |
m =1 , |
|||||
X |
= 0 , Y |
||||||||||
|
|
|
|
σy = −q |
, |
|
(3) |
||||
|
|
|
|
τxy = 0 . |
|
(4) |
|||||
При y = 0 уравнение (4) удовлетворяется тождественно при любых значениях постоянной A , а уравнение (3) приводится к виду AB = −q , откуда следует
A = −q / B .
Подставим формулы для напряжений (с учетом соотношения y = −xtgβ ) в уравнение (1). Будем иметь:
|
|
x(− xtgβ) |
|
|
|
|
|
|
|
|
x |
2 |
2 |
β |
|
|
|||
A −arctg(− tgβ)− |
|
+C |
sinβ + |
|
− A |
|
|
tg |
cosβ = 0 |
. |
|||||||||
|
|
2 |
|
2 2 |
|
|
|
|
|
|
|
2 |
|
|
2 |
2 |
|
|
|
x |
|
+ x tg β |
|
|
|
|
|
x + x tg β |
|
||||||||||
|
|
|
|
|
|
|
|
||||||||||||
При преобразовании полученного уравнения учтем, что |
|
|
|
|
|
||||||||||||||
|
tg2β |
|
= sin 2 β |
, |
|
tgβ |
|
= sinβcosβ . |
|
|
|||||||||
|
2 |
β |
|
2 |
|
|
|
||||||||||||
1+ tg |
|
|
|
1+ tg |
β |
|
|
|
|
|
|
|
|||||||
Будем иметь: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A (βsinβ+sin2 βcosβ+C sinβ−sin2 βcosβ)= 0 |
|
|
|
|
С = −β . |
|
|||||||||||||
Преобразование уравнения (2) позволяет привести его к виду:
A (−sin βsin 2 β+βcosβ+ B cosβ−sin βcos2 β)= 0 |
|
B = tgβ−β . |
43
С учетом найденного значения постоянной B определяем постоянную A . Бу-
дем иметь: |
|
|
|
|
|
A = − |
q |
. |
|
|
tgβ−β |
|||
|
|
|
|
|
|
|
|||
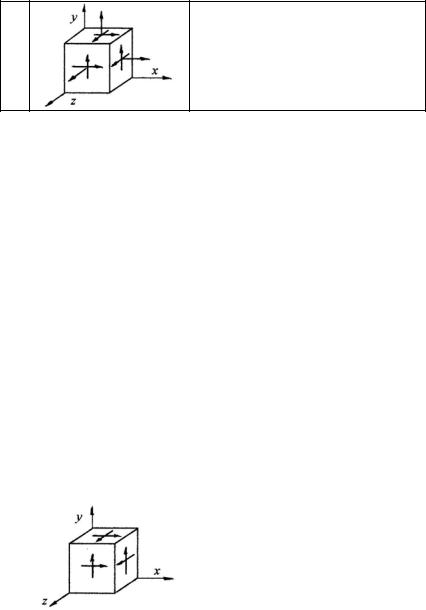
2.4. |
Провести преобразования некоторых компонентов тензора на- |
|||
|
пряжений, например σz |
и |
τxy , при повороте системы прямо- |
|
|
угольных координат xyz |
вокруг оси y на 180°. |
||
|
|
|
|
|
Указание. Использовать формулы преобразования компонентов напряженного состояния при переходе от одной системы прямоугольных координат к другой.
2.5. |
Используя формулы для преобразования компонентов напря- |
|
жений при переходе от одной прямоугольной системы координат |
|
к другой, показать, что чистый сдвиг может быть получен с по- |
|
мощью равномерного растяжения ( + q ) и равномерного сжатия |
|
( −q ) в двух взаимно перпендикулярных направлениях. |
|
|
Равномерное растяжение ( + q ) и равномерное сжатие ( −q ) в двух взаимно
перпендикулярных направлениях реализуем в главной системе координат 1, 2, 3, принимая σ1 = q , σ2 = 0 , σ3 = −q . Будем считать, что чистый сдвиг реализуется
в системе координат xyz , полученной из главной системы координат поворотом на угол α вокруг оси 2 (ось z совпадает с осью 2), на площадке, перпендикулярной оси x . Направляющие косинусы, определяющие положение осей x, y, z в системе координат 1, 2, 3, приведены в табл. 2.2.
|
|
|
Таблица 2.2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
3 |
|
|
|
Учитывая значения направляющих косину- |
||
x |
cosα |
|
|
0 |
sin α |
|
|
|
||||
|
|
|
|
сов, для напряжений на площадке, перпендику- |
||||||||
y |
−sin α |
|
|
0 |
cosα |
|
|
|||||
|
|
|
|
лярной оси x, имеем: |
|
|||||||
z |
0 |
|
|
0 |
|
1 |
|
|
|
|
|
|
|
|
σ |
x |
= σ l2 |
+σ m2 |
+σ |
3 |
n2 = q cos2 α−qsin2 α = 0 , |
||||
|
|
|
1 |
1 |
1 |
1 |
|
1 |
|
|||
|
τxy = σ1l1l 2 +σ1m1m 2 +σ3n1n 2 = −q cosαsin α −qsin αcosα = τ . |
|||||||||||
Из |
первого соотношения |
следует, что угол поворота |
должен быть равен |
|||||||||
α = π/ 4 , а из второго – значение касательного напряжения: |
τ = −q . |
|||||||||||
44
2.6.
Задан тензор напряжений, все компоненты которого равны величине a . Определить тип напряженного состояния.
Тип напряженного состояния (одноосное, двухосное, трехосное) определяется числом главных нормальных напряжений, отличных от нуля.
Выпишем уравнение, определяющее главные нормальные напряжения:
σ3 − JIσσ2 + JIIσσ− JIIIσ = 0 ,
где коэффициенты уравнения являются инвариантами тензора напряжений:
JIσ = σx +σy +σz ,
JIIσ = σxσy +σyσz +σzσx −τ2xy −τ2yz −τ2zx ,
JIIIσ = σxσyσz +2τxyτyzτzx −σxτ2yz −σyτ2zx −σzτ2xy .
Вычислим коэффициенты уравнения (инварианты) в соответствии с условием задачи. Будем иметь:
JIσ = 3a , JIIσ = JIIIσ = 0 .
Уравнение для определения главных нормальных напряжений принимает вид:
σ3 −3aσ2 = 0 |
σ = 3a |
, |
σ |
2 |
= σ |
3 |
= 0 . |
|
1 |
|
|
|
|
Следовательно, напряженное состояние – одноосное.
2.7. |
|
Задан тензор напряжений, в ко- |
|
|
|
|
|
тором все нормальные напряжения |
|
|
равны нулю, а касательные напря- |
|
|
жения равны τ . Определить тип на- |
|
|
пряженного состояния. |
|
|
|
Вычислим инварианты тензора напряжений в соответствии с условием задачи.
45
