(σ1 − σ2) (l1l 2 + m1m2 + n1n2 )= 0 .

Поскольку в общем случае главные напряжения имеют разные значения, получаем, что

l1l2 + m1m2 + n1n2 = 0 .

Известно, что данное условие определяет перпендикулярность двух прямых в пространстве, а в нашем случае – перпендикулярность двух главных площадок, что и требовалось доказать.

При совмещении направления осей координат с направлениями главных нормальных напряжений можем говорить о главных осях 1, 2, 3 тензора напряжений (обозначения для главных осей будем вводить по индексам главных напряжений).

В главных осях представления тензора напряжения и его инвариантов значительно упрощаются:

Не стоит, однако, думать, что напряженное состояние в главных осях определяется только тремя величинами: σ1 , σ2 , σ3 . Для пе-

рехода к главным осям необходимо располагать также значениями направляющих косинусов одной из главных площадок l , m , n , откуда следует, что и здесь число неизвестных равно шести.

В частных случаях главные напряжения могут принимать значения, равные нулю. По числу главных напряжений, отличных от нуля, различают три типа напряженного состояния в данной точке: одноосное, двухосное и трехосное.

2.4.3. Исследование касательных напряжений

Рассмотрим теперь вопрос об экстремальных значениях касательных напряжений. Будем считать, что координатные оси являются главными осями тензора напряжений. Рассмотрим произ-

30

вольную площадку с нормалью n , которая имеет направляющие косинусы l , m , n с главными осями 1 , 2 , 3 соответственно. Касательное напряжение на этой площадке можем определить с по-

мощью известной формулы τn2 = pn2 −σn2 .

Поскольку рассматриваем площадку в главных осях, касатель-

С учетом соотношений, полученных для напряжений pn и σn , касательное напряжения τn будет иметь вид:

Представленное соотношение позволяет рассматривать касательное напряжение τn как функцию переменных l , m , n и ис-

кать те площадки, на которых τn достигает экстремума. Так же,

как и в случае определения экстремальных значений нормальных напряжений, нужно учесть, что направляющие косинусы связаны условием l 2 + m 2 + n 2 =1 .

Поставленную задачу будем решать, исключая с помощью имеющегося условия одну переменную и рассматривая τn уже как

функцию только двух переменных. Так, например, исключая n , получим, что

31

Дифференцируем полученное соотношение по l и по m. Соответственно имеем:

2τn ∂∂τln = 2l (σ12 −σ32 )−

−2[(σ1 −σ3 )l2 +(σ2 −σ3 )m2 +σ3 ] 2l (σ1 −σ3 ) , 2τn ∂∂τmn = 2m (σ22 −σ32 ) −

−2[(σ1 −σ3 )l2 +(σ2 −σ3 )m2 +σ3 ] 2 m(σ2 −σ3 ) .

Деление на τn в полученных соотношениях возможно, так как значение τn = 0 определяет главную площадку, свойства которой

уже известны. Проведя некоторые преобразования, запишем теперь уравнения, определяющие условия экстремума функции τn :

имеют неодинаковые значения, необходимые условия экстремума можно переписать в форме:

32

Полученная система уравнений имеет очевидное нулевое решение l = m = 0 и, соответственно, n = ± 1, но это решение определяет главную площадку. Соответственно, ненулевые решения для переменных m и l удовлетворяют уравнениям:

Для данной системы уравнений возможны три варианта решений:

1) l ≠ 0, m = 0 ; 2) l = 0, m ≠ 0 ; 3) l ≠ 0, m ≠ 0 .

Отметим, что если рассматриваем решение 1, то нельзя пользоваться вторым уравнением, так как оно получено в предположении, что m ≠ 0 (справедливо первое уравнение), а если рассматриваем решение 2, то нельзя пользоваться первым уравнением, так как оно получено в предположении, что l ≠ 0 (справедливо второе уравнение). Решение l ≠ 0, m ≠ 0 приводит к условию σ1 −σ2 = 0 , но это

частный случай, который не рассматриваем.

Рассмотрим вначале второй вариант решения l = 0, m ≠ 0 . Из второго уравнения будем иметь:

Третий направляющий косинус находим из условия n2 =1 − l 2 − m2 n = ±1/ 2 .

Считая площадку с найденными направляющими косинусами первой, определим на ней экстремальное (главное) значение τ1 ,

используя исходное уравнение для τ2n . Будем иметь:

33

Рассматривая вариант решения l ≠ 0, m = 0 , получим вторую площадку с направляющими косинусами

l = ±1/ 2 , m = 0 , n = ±1/ 2 ,

на которой действует главное касательное напряжение

τ2 = ± (σ3 −σ1)/ 2 .

Если из уравнения для касательного напряжения τ2n исключим не n , а m или l , то получим дополнительно ещё одно решение:

l = ±1/ 2 , m = ±1/ 2 , n = 0 τ3 = ±(σ1 −σ2 )/ 2 .

На основании полученных решений можем сделать следующий вывод:

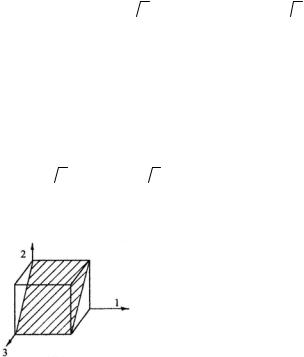
главное касательное напряжение равно полуразности главных нормальных напряжений и принадлежит площадке, нормаль к которой перпендикулярна одной из главных осей и делит угол между двумя другими главными

Одно из этих главных касательных напряжений является наибольшим и равно по величине

емся, что на тех площадках, где касательные напряжения достигают экстремума, нормальные напряжения отличны от нуля.

34