2.4.Анализ напряженного состояния в точке

2.4.1.Преобразование компонентов напряженного состояния при замене системы прямоугольных координат

Напряженное состояние в произвольной точке тела при данном выборе прямоугольной системы координат определяется шестью компонентами напряжений, действующими на трёх взаимно перпендикулярных площадках, проходящих через эту точку и параллельных координатным плоскостям.

Если же в этой точке ввести другую («новую») систему координат, то напряженное состояние будет определяться шестью «новыми» компонентами напряжений, которые должны определяться через шесть «старых».

Обозначим старую координатную систему как x, y, z , а новую – x′, y′, z′. Соответственно, компоненты напряжений в старой системе будут σx , σy , τxy и т.д., а в новой − σx′ , σy′, τx′y′ и т.д.

Пусть ориентация осей x′, y′, z′ относительно осей x, y, z задана направляющими косинусами, представленными в табл. 2.1.

Проекции полного напряжения на элементарной площадке, перпендикулярной к оси x′, на старые оси x, y, z можно вычислить по известным формулам:

X x′ = σxl1 + τyxm1 + τzx n1 ,

Yx′ = τxyl1 + σy m1 + τzy n1 ,

Z x′ = τxzl1 + τyz m1 + σz n1 .

Аналогично можем записать проекции полных напряжений, действующих на элементарных площадках, перпендикулярных осям y′, z′.

23

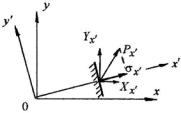
Чтобы получить проекции полных напряжений, действующих на площадках, перпендикулярных к осям x′, y′, z′, на новые оси

x′, y′, z′, воспользуемся тем, что проекция равнодействующей на

какое-либо направление равна сумме проекций её компонентов на это же направление. Так, проектируя полное напряжение, дейст-

легко получить с использованием круговой замены индексов.

Отметим, что полученные соотношения отвечают формулам преобразования компонентов тензора второго ранга, симметрично-

24

го относительно главной диагонали, при замене системы прямоугольных координат. Соответственно, можно говорить о тензоре напряжений как о тензоре второго ранга, симметричном относительно главной диагонали.

2.4.2. Исследование нормальных напряжений

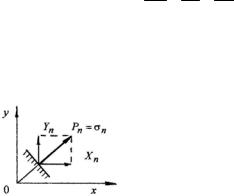
Интерес с точки зрения прочности представляет не полное напряжение на какой-либо площадке с нормалью n , а его составляющие σn и τn (нормальное и касательное напряжения) и, в частности, экстремальные значения этих напряжений.

Покажем, что в точке тела существуют такие три взаимно перпендикулярные площадки, на которых нормальные напряжения принимают экстремальные (стационарные) значения, а касательные напряжения равны нулю.

Рассмотрим произвольную площадку с нормалью n , имеющей направляющие косинусы l , m , n . Нормальное напряжение на этой площадке представляется в виде:

σn = σxl 2 + σym2 + σzn2 + 2τxylm + 2τyzmn + 2τzxnl .

Выписанное соотношение можно рассматривать как функцию трех переменных l , m , n , которые связаны между собой извест-

ной формулой l 2 + m2 + n2 =1. Соответственно, чтобы найти стационарные значения функции σn = σn (l , m , n), нужно решать задачу на условный экстремум.

Для решения поставленной задачи составляется вспомогательная функция

F (l, m, n, λ)= σn + λ(l 2 + m2 + n2 −1)= λ(l 2 + m2 + n2 −1)+ + σxl 2 + σy m2 + σz n2 + 2τxy l m + 2τyz m n + 2τzx n l ,

частные производные которой по переменным l , m , n приравниваются нулю:

25

∂F / ∂l = 2σxl + 2τxy m + 2τzxn + 2lλ = 0 , ∂F / ∂m = 2σym + 2τxyl + 2τyz n + 2mλ = 0 , ∂F / ∂n = 2σz n + 2τyz m + 2τzx l + 2nλ = 0 .

Полученные три уравнения вместе с условием l 2 + m2 + n2 =1 составляют полную систему уравнений для отыскания всех четырех неизвестных l , m , n и λ, определяющих стационарные значения функции F и, соответственно, нормального напряжения σn .

Представленных условий экстремума достаточно, чтобы, не решая их, сделать некоторые выводы. Перепишем уравнения в форме:

(σxl + τxy m + τzx n) / l = −λ , (σy m + τxyl + τyz n) / m = −λ , (σz n + τyz m + τzx l) / n = −λ .

Можно видеть, что числители полученных соотношений определяют составляющие полного напряжения X n , Yn , Zn на рас-

сматриваемой площадке и, таким образом, условия экстремума функции F приводятся к соотношениям

Xln = Ymn = Znn = const .

Полученные равенства показывают, что на площадке, где функция F (или нормальное напряжение σn ) имеет стационарное

значение, компоненты полного напряжения должны быть пропорциональны направляющим косинусам нормали к площадке.

Указанная ситуация реализуется, когда полное напряжение направлено по нормали к этой площадке (рис. 2.6). Действительно, в этом случае

26

Но если полное напряжение направлено по нормали к площадке, то на этой площадке касательное напряжение равно нулю.

Таким образом, мы доказали, что действительно существуют такие площадки, где нормальное напряжение имеет стационарное значение и где касательное напряжение равно нулю. Эти площадки называют главными площадками, а соответствующие нормальные напряжения − главными.

Теперь остается определить, сколько может быть главных площадок и, соответственно, главных нормальных напряжений в любой точке тела.

Пусть имеем главную площадку с нормалью n и направляющими косинусами l , m , n . Величина главного (полного) напряжения на ней равна σ. Запишем проекции этого напряжения на координатные оси.

С одной стороны, эти проекции можно определить непосредственно:

X n = σl , Yn = σm , Zn = σn .

С другой стороны, эти же проекции можем записать по известным формулам:

X n = σxl + τyxm + τzx n ,

Yn = τxyl + σy m + τzy n ,

Z n = τxzl + τyz m + σz n .

Из сопоставления приведенных соотношений следует, что

τxzl + τyz m + (σz − σ) n = 0 .

Полученную систему уравнений можно рассматривать как систему уравнений для отыскания направлявших косинусов l , m , n площадок, на которых действуют главные нормальные напряжения. Рассматриваемые уравнения являются линейными и однород-

27

ными относительно неизвестных l , m , n , и могут дать решения, отличные от нуля, только в том случае, если определитель системы уравнений равен нулю (нулевое решение системы не рассматриваем, поскольку направляющие косинусы l , m , n связаны соотно-

шением l 2 + m2 + n2 =1). Вычисляя определитель системы и приравнивая его нулю, приходим к следующему уравнению относительно главного напряжения σ:

σ3 – ( σx + σy + σz ) σ2 + ( σxσy + σyσz + σzσx – τ2xy – τ2yz – τ2zx ) σ −

− ( σxσyσz + 2 τxyτyzτzx – σxτ2yz – σyτ2zx – σzτ2xy ) = 0 .

Полученное уравнение имеет три действительных и, в общем случае, три различных корня (соответствующее математическое доказательство имеется). Эти три корня определяют значения трех главных нормальных напряжений σ1 , σ2 , σ3 , которым соответст-

вуют три группы направляющих косинусов li , mi , ni ( i = 1, 2, 3)

для трех главных площадок. В общем случае индексы 1, 2, 3 присваиваются главным напряжениям так, чтобы выполнялись неравенства σ1 ≥ σ2 ≥ σ3 .

По определению главные нормальные напряжения так же, как и ориентация соответствующих им главных площадок, должны сохраняться в данной точке без изменения при любом преобразовании системы координат x, y, z . Следовательно, они обладают

свойством инвариантности по отношению к выбору (или повороту) осей x, y, z . Для обеспечения указанного свойства необходимо,

чтобы коэффициенты при σ в уравнении являлись инвариантами относительно ортогонального преобразования координат.

Выпишем эти коэффициенты, которые в дальнейшем будем называть инвариантами тензора напряжений:

I1σ = σx + σy + σz ,

I2σ = σxσy + σyσz + σzσx – τ2xy – τ2yz – τ2zx ,

I σ = σ σ σ + 2 τ τ τ – σ τ2 – σ τ2 – σ τ2 .

3 x y z xy yz zx x yz y zx z xy

28

Первый из них называется линейным инвариантом, второй – квадратичным и третий – кубичным.

Значения направляющих косинусов l , m , n , определяющие одну из главных площадок, находим с помощью двух уравнений из

системы и уравнения l 2 + m 2 +n 2 =1. Третье уравнение системы «пропадает» в силу равенства нулю определителя системы.

Исследования полученных значений li , mi , ni ( i = 1, 2, 3) по-

казывают, что главные площадки, соответствующие найденным главным напряжениям σi ( i = 1, 2, 3) взаимно перпендикулярны.

Ортогональность главных площадок можно показать следующим образом. Для первой площадки имеем:

σ1 l1 = σxl1 + τyx m1 + τzx n1 , σ1 m1 = τxyl1 + σy m1 + τzy n1 , σ1 n1 = τxzl1 + τyz m1 + σz n1 .

Умножим первое уравнение на l 2 , второе – на m2 , третье – на n 2 и сложим. Получим:

σ1(l1l2 + m1m2 + n1n2 )=

= σxl1l2 + σym1m2 +σzn1n2 + τxy (m1l2 + m2l1)+...

Аналогичная процедура для второй площадки, но с умножением первого уравнения на l1 , второго – на m1 , третьего – на n1 , позво-

ляет получить

σ2 (l1l2 + m1m2 + n1n2 )=

= σxl1l2 + σym1m2 + σzn1n2 + τxy (m1l2 + m2l1)+...

Теперь вычтем из уравнения, полученного для первой площадки, уравнение, полученное для второй. Будем иметь:

29