Из граничных условий в напряжениях на боковой поверхности вала остается только одно уравнение:

Под плоской задачей теории упругости понимают совокупность двух родственных в математическом отношении задач:

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Sapunov_Prikladnaya_teoriya_uprugosti_ch1_2008.pdf

Скачиваний:

248

Добавлен:

05.06.2015

Размер:

4.18 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 1819 / 2019 20 > Следующая >>>

которое можно представить в виде:

∂	(r2τrθ)+	∂	(r2τθz )= 0 .
∂r		∂z

Функция напряжений ϕ = ϕ(r , z) вводится так, чтобы удовлетворить дифференциальное уравнение равновесия:

τrθ = −	1	∂ϕ	,	τθz =	1	∂ϕ .
	r2 ∂z
					r2 ∂r

Уравнение, определяющее функцию напряжений, должны получить из уравнений Бельтрами – Митчелла. Поскольку в рассматриваемой задаче имеем достаточно простые поля деформаций и напряжений, получим вначале условие совместности деформаций, исключая перемещение v из соотношений для деформаций γrθ и

γθz . Будем иметь:

γrθ =	∂v		−	v	= r		∂ v
	∂r			r

							∂r r
		∂v				∂		v
γθz	=			= r

		∂z
						∂z r

∂	γrθ		∂	γθz
		−			= 0 .

∂z	r		∂r	r

Переходя в условии совместности деформаций к напряжениям и подставляя затем их значения через функцию напряжений, приходим к уравнению, определяющему функцию напряжений:

∂

∂ϕ

∂

∂ϕ

∂

3 ∂ϕ

∂

−

= 0

−

= 0 .

∂z

∂r

∂r2

∂r

∂z2

∂z

∂r r3

τrθ l + τzθ n = 0 .

164

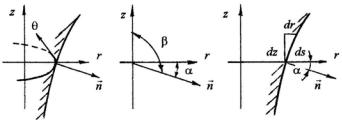
Направляющие косинусы нормали к площадке, расположенной на боковой поверхности скручиваемого вала, определим следующим образом (рис. 10.1):

Рис. 10.1

Непосредственно из рис. 10.1 для направляющих косинусов имеем:

l = cos (−α)= cosα = dz / ds ,

n = cos (−β)= cos (90 +α)= −sin α = − dr / ds .

Соответственно, граничное условие на боковой поверхности вала (на его контуре или на образующей) для функции напряжений будет иметь вид:

∂ϕ d r	+	∂ϕ d z	= 0	d ϕ	= 0	ϕ = const .
				d s
∂r d s		∂z d s

Таким образом, решение задачи о кручении круглых валов переменного диаметра сводится к отысканию функции напряжений ϕ, удовлетворяющей дифференциальному уравнению

∂2 ϕ	−	3	∂ϕ	+	∂2	ϕ	= 0
∂r2		r	∂r		∂z2

и граничному условию ϕ = const на контуре вала. 165

Значение крутящего момента в произвольном поперечном сечении легко вычислить:

a	a	∂ϕ dr = 2πϕ	0a = 2π[ϕ(a , z)−ϕ(0, z)] .
M = ∫τzθ r 2πrdr = 2π∫
		∂r
0	0

Для решения задач, с которыми приходится сталкиваться на практике, обычно применяют численные методы.

Задача

10.1.

Решить задачу о кручении вала конической формы

Напомним, что задача о кручении круглых валов переменного диаметра (тел вращения) сводится к отысканию функции напряжений ϕ = ϕ(r , z), удовлетво-

ряющей дифференциальному уравнению

∂2 ϕ	−	3	∂ϕ	+	∂2	ϕ	= 0
∂r2		r	∂r		∂z2

и граничному условию ϕ = const на контуре вала.

Значение крутящего момента в произвольном поперечном сечении при найденной функции напряжений определяется соотношением

M = 2π[ϕ (a, z)− ϕ (0, z)] .

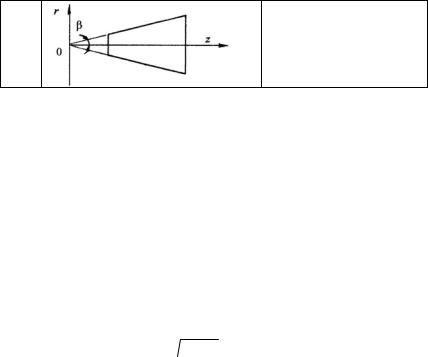
Уравнение контура вала конической формы имеет вид:

z / r 2 + z2 = cos β ,

причем отношение, фигурирующее в левой части уравнения, является величиной постоянной. Соответственно, если функцию напряжений ϕ строить как функцию

этого отношения, то граничное условие на контуре ϕ = const будет удовлетворе-

но.

Легко проверить, что функция

166

		z		1	z	3
ϕ = С			−				,

		+ z2		3	r2 + z2
	r2

где С − постоянная, удовлетворяет дифференциальному уравнению, определяющему функцию напряжений ϕ . Постоянную С определим, считая, что значение

крутящего момента в произвольном поперечном сечении задано. В этом случае будем иметь:

			z			1			z		3		1		3M
M = 2πС					−							−1+		C =−			.
		2		2		3		2		2			3		2π (2−3cosβ+cos3
	a		+ z				a		+ z							β)

Вычисление касательных напряжений приводит к следующим соотношениям:

τrθ = −	C r2	, τθz = −		C r z	,
	(r2 + z2) 5 / 2		(r2	+ z2) 5 / 2

где постоянная С определяется вышеприведенной формулой.

11. Плоская задача теории упругости

(ϕ)1 = M1 ,

-задачи о плоском деформированном состоянии (о плоской деформации);

-задачи о плоском напряженном состоянии.

11.1. Основные уравнения плоской деформации

Будем считать, что тело находится в состоянии плоской деформации, параллельной плоскости xy , если компонента полного пе-

ремещения w равна нулю, а компоненты u и v являются функциями переменных x и y :

u = u (x, y) , v = v (x, y) , w = 0 . 167

В этом случае деформации εx , εy

и γxy

будут функциями пере-

менных x и y :

εx = ∂u

εy

∂v

γxy

∂u

∂v

∂y

∂x

а деформации εz , γ yz

и γzx

− равны нулю. Соответственно, зави-

симости Коши будут представлены только тремя вышеприведенными уравнениями.

При имеющих место деформациях, из шести уравнений совместности деформаций Сен-Венана удовлетворяются тождественно пять. Оставшееся уравнение связывает деформации, отличные от

нуля:
	∂2εx	+	∂2εy	=	∂2 γxy	.
	∂y 2		∂x2
					∂x∂y

Запишем уравнения линейного физического закона. Отметим, что соотношение εz = 0 позволяет исключить напряжение σz из

этих уравнений и, соответственно, из числа определяемых неизвестных. Действительно,

εz =	1	[σz −ν(σy + σx )]= 0 σz = ν(σy + σx ) .
	E

С учетом соотношения, полученного для напряжения σz , уравнение, определяющее деформацию εx , принимает вид:

	1	[σx −ν(σy + σz )]		1	−ν2		ν
εx =			εx =			σx −		σy .
	E				E		1−ν

Введем следующие обозначения:

168

E = E / (1 − ν2 ) , ν = ν / (1 − ν) G = G .

В этом случае для деформации εx имеем:

εx =(σx −ν σy )/ E .

Преобразуя с учетом введенных обозначений соотношения для εy и γxy , уравнения линейного физического закона получим в виде:

εx =(σx −ν σy )/ E	,
εy =(σy −ν σx )/ E	,

γxy = τxy / G ,

где величины E и ν можно рассматривать как некоторые новые значения упругих постоянных.

Уравнения линейного физического закона в форме Ламе для плоской деформации имеют следующий вид:

σx = λϑ + 2μεx	,
σy = λϑ + 2μεy	,
τxy = μγxy .

Поскольку напряжения σx , σy и τxy являются функциями только переменных x и y , из трех дифференциальных уравнений равновесия остается только два:


∂σx		+		∂τxy		+ X = 0 ,
	∂x	+			∂y	+ X = 0 ,
	∂x				∂y
	∂τxy		+		∂σy	+ Y = 0 ,
	∂x		+		∂y	+ Y = 0 ,
	∂x				∂y

169

причем в этих уравнениях требуется, чтобы составляющие X и Y объемной силы были функциями переменных x и y . Третье урав-

нение равновесия переходит в условие Z = 0 : составляющая Z объемной силы должна быть равна нулю.

Таким образом, получена полная система уравнений, определяющая решение задачи о плоской деформации (плоском деформированном состоянии). Отметим, однако, что вопрос о возможности реализации плоской деформации, т.е. для какой формы тела и при каком его нагружении имеет место плоская деформация, пока остается открытым.

Будем считать, что рассматриваем длинное тело цилиндрической или призматической формы с основаниями (торцами), перпендикулярными к его оси, которую примем за ось z .

Предположим, что на боковой поверхности тела действуют внешние поверхностные силы, равномерно распределенные по длине тела и перпендикулярные к его боковой поверхности, т.е.

X = X (x, y), Y =Y (x, y), Z = 0 . Будем считать, что аналогичным условиям отвечают и объемные силы: X = X (x, y), Y =Y (x, y),

Z = 0 . При таких предположениях относительно формы тела и его нагружении можно считать, что все поперечные сечения находятся в условиях плоского деформированного состояния.

Поскольку все определяемые величины, характеризующие плоскую деформацию, являются функциями переменных x и y , гра-

ничные условия на боковой поверхности сводятся к соответствующим условиям на контуре поперечного сечения:

X = σxl + τxy m ,

Y = τyxl + σy m .

Граничные условия на торцах тела определяются наличием напряжения σz . Принимая, что площадь торца мала по сравнению с

общей поверхностью тела (используя принцип Сен-Венана), эти условия запишем в интегральной форме:

170

N z = ∫∫σz dF	,
F
M x = ∫∫σz y dF	,
F

M y = ∫∫σz x dF .

Отметим, что наличие напряжения σz и, соответственно, нагрузки N z , M x , M y на торцах определяется постановкой задачи

о плоской деформации, поскольку именно наличие нагрузки на торцах обеспечивает условие εz = 0 . Однако принимая во внимание принцип независимости действия сил, задачу можно решать

для данного тела при заданных нагрузках X и Y на боковой поверхности и нулевых нагрузках на торцах − в этом случае говорят об обобщенной плоской деформации. Соответственно, решение задачи о плоской деформации получим добавлением известных решений задач о растяжении ( N z ) и чистом изгибе ( M x , M y ).

11.2. Основные уравнения плоского напряженного состояния

В задаче о плоском напряженном состоянии будем рассматривать упругое тело в форме тонкой пластины постоянной толщины h , нагруженное по боковой поверхности силами, параллельными плоскости пластины и распределенными симметрично относительно ее срединной плоскости, которую совместим с координатной плоскостью x y . Будем считать, что объемные силы отвечают ана-

логичным условиям.

Торцы (основания) пластины z = ±h / 2 свободны от нагрузки.

Граничные условия на торцах в поставленной задаче принимают вид:

σz = τzx = τzy = 0 при z = ±h / 2 .

171

Если пластину считать тонкой, то при рассматриваемом нагружении с достаточной степенью точности можно принять напряжения σz , τzx и τzy равными нулю во всех точках пластины. Ос-

тальные компоненты тензора напряжений σx , σy и τxy можно считать функциями только переменных x и y , усреднив их по

толщине пластины. Такое напряженное состояние пластины будем называть плоским напряженным состоянием. Очевидно, что при нагрузке на боковой поверхности, не меняющейся по толщине, процедуру усреднения напряжений можно опустить.

Отметим, что	при плоском напряженном состоянии имеем
σz = 0 , а εz ≠ 0	(в отличие от плоской деформации, где εz = 0 , а

σz ≠ 0 ). Наличие поперечной деформации εz влечет за собой ис-

кривление плоских оснований пластины, однако, поскольку задача симметрична, точки срединной плоскости после деформирования пластины остаются на месте. Данное обстоятельство позволяет утверждать, что при малой толщине пластины перемещение w будет весьма мало и что изменения перемещений u и v по толщине будут незначительны Соответственно, можно считать, что перемещения u и v являются функциями только переменных x и y .

Дифференциальные уравнения равновесия в задаче о плоском напряженном состоянии принимают вид:


∂σx		+		∂τxy		+ X = 0 ,
	∂x	+			∂y	+ X = 0 ,
	∂x				∂y
	∂τxy		+		∂σy	+Y = 0 .
	∂x		+		∂y	+Y = 0 .
	∂x				∂y

Граничные условия на боковой поверхности сводятся к соответствующим условиям на контуре поперечного сечения:

X = σxl + τxy m ,

Y = τyxl + σy m .

172

Отметим, что использование соотношения σz = 0 в уравнениях линейного физического закона позволяет исключить деформацию εz из этих уравнений и, соответственно, из числа определяемых неизвестных. Действительно, можем получить, что

εz =	1	[σz −ν(σx +σy )]	εz = −	ν	(σx +σy ) .
	E			E

Для определения оставшихся деформаций εx , εy и γxy ( γyz = = γzx = 0 ) имеем следующие три уравнения физического закона:

εx =	1			(σx − νσy )		,
		E
				(σy − νσx ) ,
εy =	1
		E

γxy	=		2 (1 + ν)		τxy .
				E

Использование соотношения σz = 0 в уравнениях линейного физического закона в форме Ламе позволяет получить деформацию εz в следующей форме:

σz = λ(εx + εy + εz )+ 2μεz = 0 εz = −	λ	(εx + εy ) .
	λ + 2μ

Преобразованные уравнения физического закона будут иметь вид:

σx = λ ϑ + 2μεx		,
σy = λ ϑ + 2μεy		,
τxy = μγxy	,
где ϑ = εx + εy ≠ ϑ; λ = 2λμ /(λ + 2μ)	− некоторая новая упругая
постоянная.
173

Зависимости Коши в рассматриваемой задаче будут представлены тремя уравнениями:

εx =	∂u	,	εy =	∂v	,	γxy =	∂u	+	∂v	.
	∂x			∂y			∂y
									∂x

Рассмотрение условий совместности деформаций Сен-Венана приводит к уравнению, связывающему деформации, отличные от нуля, а именно:

∂2εx	+	∂2εy	=	∂2 γxy
∂y 2		∂x2		∂x∂y

и к дополнительным условиям относительно вида функции εz :

∂ 2ε	z	= 0	,	∂ 2ε	z	= 0	,	∂ 2ε	z	= 0 .
∂x2				∂y 2				∂x∂y

Последние три соотношения определяют деформацию εz как линейную функцию переменных x и y , что входит в некоторое

противоречие			с	полученными			ранее	соотношениями:
εz = −	ν	(σx + σy )= −		λ		(εx + εy ).	Тем не	менее, учитывая
	E			λ +	2μ

малость деформации εz , будем считать эти требования выполненными.

11.3. Сопоставление уравнений плоской деформации и плоского напряженного состояния

Из сравнения уравнений, определяющих решения задач о плоской деформации и плоском напряженном состоянии, следует, что в математическом плане эти уравнения идентичны. В дальнейшем будем говорить об уравнениях плоской задачи теории упругости и ее решении, при необходимости различая задачи о плоской дефор-

174

мации и плоском напряженном состоянии по тем признакам, которые указывались при построении соответствующих уравнений.

11.4. Решение плоской задачи в напряжениях

Общая схема решения задачи теории упругости в напряжениях рассмотрена в разделе 5. Следуя этой схеме, построим соответствующее решение плоской задачи.

Для получения полной системы уравнений в напряжениях к дифференциальным уравнениям равновесия необходимо добавить условие совместности деформаций

∂2εx	+	∂2εy	=	∂2 γxy	,
∂y 2		∂x2		∂x∂y

преобразованное с использованием уравнений физического закона


εx =	1			(σx − νσy ) ,
εx =		E		(σx − νσy ) ,
		E		(σy − νσx ) ,
εy =	1
εy =		E
		E	2 (1 + ν)
γxy	=		2 (1 + ν)		τxy .
γxy	=				τxy .
				E

После преобразований условие совместности деформаций будет иметь вид:

∂

σx

∂

σy

∂

σx

∂

σy

∂

τxy

− ν

= 2 (1 + ν)

∂y

∂x

∂y

∂x∂y

Полученное соотношение упростим, заменив в его правой части касательное напряжение τxy на нормальные напряжения σx и σy .

Для этой цели используем уравнения равновесия. Дифференцируя первое из них по переменной x , а второе – по переменной y и

175

складывая их, получим

2	∂2 τxy	= −	∂2σx	−	∂2σy	−	∂X	−	∂Y .
	∂x∂y		∂x2		∂y 2		∂x
									∂y

После некоторых преобразований будем иметь:

∂X

∂Y

(σx + σy )= −(1 + ν)

∂x

∂y

где 2 =

∂2

− оператор Лапласа.

∂x2

∂y 2

Таким образом, решение плоской задачи в напряжениях сведено к решению трех следующих уравнений:

∂σx

∂τxy

+ X = 0 ,

∂x

∂y

∂τxy

∂σy

= 0

∂x

∂y

∂X

∂Y

(σx + σy )= −(1 + ν)

∂x

∂y

Полученное решение должно быть подчинено граничным условиям.

11.5. Решение плоской задачи в напряжениях с помощью функции напряжений (функции Эри)

Систему трех уравнений в напряжениях, полученную для решения плоской задачи, легко свести к одному уравнению относительно функции напряжений ϕ = ϕ(x, y), полагая, что объемные силы

X и Y равны нулю.

176

Действительно, если ввести функцию напряжений соотношениями

σx =	∂2	ϕ	,	σy =	∂2	ϕ	,	τxy = −	∂2ϕ	,
	∂y 2				∂x2				∂x∂y

то дифференциальные уравнения равновесия удовлетворяются тождественно, а третье уравнение при подстановке в него значений напряжений переходит в бигармоническое уравнение

2 2ϕ =	∂4ϕ	+ 2	∂4ϕ	+	∂4ϕ	= 0 .
	∂x4		∂x2∂y 2		∂y 4

Соответственно, граничные условия в напряжениях на контуре поперечного сечения переходят в граничные условия для функции напряжений:

∂2ϕ

l −

m = X ,

∂y 2

∂x∂y

∂2

−

l +

m =Y .

∂x∂y

∂x2

Таким образом, решение плоской задачи в напряжениях сведено к определению бигармонической функции ϕ = ϕ(x, y), удовлетво-

ряющей заданным граничным условиям на контуре поперечного сечения тела.

Отметим, что в определяющие уравнения не входят упругие постоянные материала. Данное обстоятельство позволило М. Леви в свое время сформулировать теорему:

распределение напряжений в плоской задаче при заданном нагружении на контуре является одинаковым для всех изотропных материалов.

Дж. Митчелл показал, что теорема справедлива всегда для поперечного сечения в форме односвязной области, а для сечения в

177

форме многосвязной области – только лишь в случае, когда главные векторы внешних сил, приложенных к каждому контуру, равны нулю.

Теорема Леви − Митчелла является основой оптического метода исследования напряжений в элементах конструкций, поскольку позволяет изучать напряженное состояние на моделях из материалов, оптически чувствительных к возникающим в них напряжениям.

11.5.1. Свойства функции напряжений

Решение плоской задачи в напряжениях сведено к отысканию бигармонической функции ϕ = ϕ(x, y), удовлетворяющей задан-

ным граничным условиям на контуре поперечного сечения тела. Поскольку напряженное состояние определяется вторыми произ-

водными функции		напряжений,			очевидно, что функция
ϕ1	(x, y)= ϕ(x, y)+ ax + by + c при любых					значениях постоянных
a,	b, c также будет функцией напряжений для данной задачи.
				Имеющимся произволом в вы-
			боре постоянных a, b, c распоря-
			димся для задания в некоторой точ-
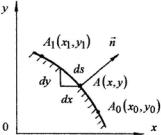
			ке	A0 (x0 , y0 ), находящейся на
			контуре односвязного поперечного
			сечения тела (рис. 11.1), нулевых
			значений функции напряжений и ее
	Рис. 11.1		первых производных:
	(ϕ)0 = 0		∂ϕ			∂ϕ
		,		= 0 ,			= 0 .
		,		= 0 ,			= 0 .
			∂x 0			∂y 0

Определим значения функции напряжений и ее первых производных в точке A1(x1, y1 ), также расположенной на контуре попе-

речного сечения. При движении от точки A0 к точке A1 выбираем

положительное направление обхода контура, при котором тело остается слева.

178

Поскольку рассматриваемые точки находятся на контуре поперечного сечения, для решения поставленного вопроса воспользуемся граничными условиями для функции напряжений:

∂2ϕ

l −

m = X

∂y 2

∂x∂y

∂2

−

l +

m =Y

∂x∂y

∂x2

которые с учетом значений направляющих косинусов ( l = d y / d s , m = −d x / d s ) перепишем в следующем виде:

∂

∂ϕ

∂

∂ϕ

d y

d x

= X

= X .

∂y

d s

∂x

d s

∂

∂ϕ

∂

∂ϕ

−

d y

−

∂ϕ d x

= −Y .

∂x

∂y

d s

∂x ∂x d s

d s

Интегрируя полученные соотношения на интервале от S = 0 до

S = S1 ,

где

S1 = A0 A1 ,

находим значения

первых

производных

функции напряжений в точке A1 :

∂ϕ

∫X d s = Rx ,

∂y

∂ϕ

= − ∫Y d s = −Ry

∂x

где Rx

− проекции на оси x и

y главного вектора внешней

нагрузки, приложенной к участку контура A0 A1 .

Запишем теперь производную функции напряжений ϕ(x, y) по переменной s . Будем иметь:

179

d ϕ

∂ϕ

d x

∂ϕ d y

d ϕ

d x

d y

= −

d s +

∫

d s .

∫Y

∂y d s

d s

∂x d s

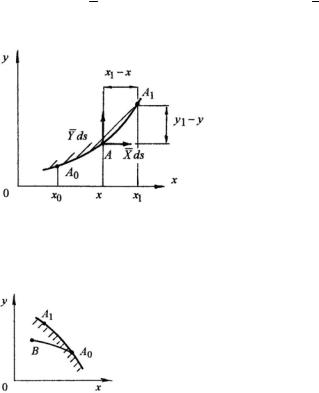
Для получения значения функции напряжений в точке A1 интегрируем выписанное соотношение по частям:

d x

d y

ϕ1 = ∫

−

∫Y d s +

∫

X d s d s

= − x

∫Y d s + y

∫

X d s

−

d s

− S∫1(− xY

+ y

)d s = S∫1 [(y1 − y )

−(x1 − x)Y

]d s = M1 .

В полученном соотношении подынтегральное выражение определяет момент внешней нагрузки, действующей на элементе дуги контура d s относи-

	тельно	точки A1	(рис. 11.2),
	причем	момент,	вращающий
	против часовой стрелки, счита-
Рис. 11.2	ется положительным.

Следовательно, значение функции напряжений в точке A1 контура равно моменту нагрузки, приложенной к участку контура A0 A1 , относительно точки A1 .

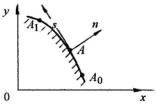
	Приведенные рассуждения применимы и
	для определения значений функции напряже-
	ний и ее первых производных в любой внут-
	ренней точке B (рис. 11.3). Однако в этом слу-
	чае должны говорить о части тела, располо-
	женной слева от A0 B , и об упругих внутрен-
Рис. 11.3	них силах, приложенных к линии A0 B .
	180

Во многих случаях удобнее пользо-
ваться более общими формулами, оп-
ределяющими функцию напряжений и
ее первые производные на контуре од-
носвязного поперечного сечения, в сис-
теме координат, связанной с направле-
ниями нормали и касательной в данной	Рис. 11.4
точке контура (рис. 11.4). В этом случае имеем:

Здесь Rn , Rs − проекции главного вектора внешней нагрузки, действующей на участке контура A0 A1 на направления внешней нормали и касательной к контуру; M1 − момент этой же внешней нагрузки относительно точки A1 (знаки взяты для положительного обхода контура).

Представленные зависимости, определяющие функцию напряжений и ее первые производные в произвольной точке контура односвязного поперечного сечения, по смыслу являются граничными условиями для функции напряжений ϕ(x, y). Можно показать, что

из трех условий независимыми являются только два, а именно: (ϕ)1 = M1 и (∂ϕ/ ∂n)1 = − R s . Действительно, здесь достаточно

вспомнить, что соотношение (ϕ)1 = M1 получено интегрировани-

ем производной ∂ϕ/ ∂s . Таким образом, решение плоской задачи с

использованием граничных условий в полученной форме сводится к отысканию бигармонической функции ϕ(x, y) по значениям этой

функции и ее производной по нормали к контуру поперечного сечения, заданным на контуре.

Для односвязной области главный вектор и главный момент нагрузки, приложенной к контуру, равны нулю. Следовательно, значения функции напряжений ϕ и ее нормальной производной

∂ϕ/ ∂n после обхода контура возвращаются к исходным нулевым значениям – функция напряжений в этом случае однозначна.

181

Если же рассматриваемая область (поперечное сечение тела) многосвязная, то значения ϕ и ∂ϕ/ ∂n после обхода какого-либо

из контуров будут совпадать с исходными (не обязательно нулевыми, поскольку задание нулевых значений функции напряжений и ее первых производных возможно только на одном из контуров), только в том случае, если внешняя нагрузка на этом контуре статически эквивалентна нулю. В противном случае при обходе контура ϕ и ∂ϕ/ ∂n получают приращения − функция напряжений для

многосвязной области может быть многозначной.

Отметим, что многозначность функции напряжений не означает многозначность напряжений – в принципе, любая гармоническая функция определяет действительное напряженное состояние, однако при этом перемещения в случае многосвязной области могут быть многозначными.

11.6. Плоская задача в полярных координатах

Во многих случаях решение плоской задачи строится проще, если вместо прямоугольной системы координат применять подобранную соответствующим образом систему криволинейных координат. В частности, для тел, имеющих круговое очертание (круговые диски и кольца, толстостенные трубы и т.п.) удобно использовать цилиндрическую (полярную) систему координат.

11.6.1. Уравнения плоской задачи в полярных координатах

	Координаты точки в поляр-
	ной	системе координат будем
	определять радиусом r и углом
	ϑ (рис. 11.5). Из компонентов
	тензора напряжений в уравне-
	ния войдут σr , σϑ и τrϑ .
	Деформированное		состояние
	в	точке будет определяться
Рис. 11.5	деформациями εr ,		εϑ , γrϑ и
	182

перемещениями u и v . Все перечисленные величины являются функциями переменных r и ϑ.

Выпишем уравнения, определяющие решение плоской задачи в полярных координатах:

- дифференциальные уравнения равновесия

∂σr

∂τrϑ

σr − σϑ

+ F = 0 ,

∂r

r ∂ϑ

∂τrϑ

∂σϑ

+ 2

τrϑ

+ F = 0

∂r

r ∂ϑ

где Fr и Fϑ − проекции объемной силы на направления r

и ϑ;

- зависимости Коши

εr =

∂u

∂r

εϑ

∂v

r ∂ϑ

γrϑ =

∂u

+ ∂v

−

;

r ∂ϑ

∂r

- условие совместности деформаций

∂2εϑ

∂εϑ

∂2εr

−

∂εr

∂2 γrϑ

∂γrϑ

;

∂r 2

r ∂r

r 2∂ϑ2

r∂r∂ϑ

r 2 ∂ϑ

r ∂r

- уравнения линейного физического закона

εr =(σr −νσϑ)/ E ,

εϑ = (σϑ −νσr )/ E ,

γrϑ = τrϑ / G

;

183

- граничные условия на боковой поверхности (на контуре поперечного сечения)

Fr = σr l + τrϑm ,

Fϑ = τrϑl + σϑm ,

где Fr и Fϑ − проекции внешней поверхностной нагрузки на направления r и ϑ.

В полярной системе координат так же, как и в прямоугольной, при отсутствии объемных сил решение плоской задачи в напряжениях сводится к решению одного уравнения относительно функции напряжений. Получение «разрешающего» уравнения в полярной системе координат ведется в той же последовательности:

-в уравнении совместности деформаций деформации заменяются на напряжения с использованием линейного физического закона;

-вводится функция напряжений ϕ (r , ϑ) так, чтобы удовлетворить тождественно дифференциальные уравнения равновесия:

σr =

∂ϕ

∂2ϕ

∂r

r 2

∂ϑ2

σϑ =

∂2

∂r

τrϑ =

∂ϕ

−

∂2ϕ

;

r 2 ∂ϑ

r ∂r ∂ϑ

- напряжения, представленные через функцию напряжений, вводятся в преобразованное уравнение совместности деформаций.

Окончательным результатом будет бигармоническое уравнение относительно функции напряжений ϕ (r , ϑ)

2 2ϕ = 0 ,

184

где 2 =	∂2	+	1 ∂	+	1	∂2	− оператор Лапласа в полярных ко-

	∂r 2		r ∂r		r 2	∂ϑ2

ординатах.

Решение бигармонического уравнения должно быть подчинено граничным условиям на контуре поперечного сечения тела.

11.6.2.Общее решение осесимметричных задач

Вслучае круговой (осевой) симметрии тела и приложенной нагрузки параметры напряженно-деформированного состояния не будут зависеть от переменной ϑ. В этом случае плоская задача из

двумерной переходит в более простую одномерную, которая описывается обыкновенным дифференциальным уравнением:

2 2

d 2

1 d

d 2

1 d ϕ

ϕ =

= 0 .

d r

r d r d r

r d r

Раскрывая операторы Лапласа, будем иметь:

d 4ϕ

2 d 3 ϕ

−

1 d 2ϕ

d ϕ

= 0 .

d r 4

d r 3

r 2

d r 2

r 3

d r

Некоторая сложность в решении полученного уравнения заключается в том, что его коэффициенты являются переменными величинами, однако введение новой переменной t = ln r позволяет перейти к обыкновенному дифференциальному уравнению с постоянными коэффициентами. Будем иметь:

d 4ϕ	− 4	d 3	ϕ	+ 4	d 2	ϕ	= 0 .
dt 4		dt	3		dt	2

Соответствующее характеристическое уравнение имеет вид:

k 2 ( k 2 −2) 2 = 0 .

185

Вычисляя корни характеристического уравнения, получим:

k1,2 = 0 , k 3,4 = 2 ,

что позволяет записать общее решение дифференциального уравнения в следующей форме

ϕ = C1 t e2t + C2 e2t + C3 t + C4 .

Переходя к исходной переменной r , получаем искомое общее решение осесимметричной плоской задачи:

ϕ = C1 r 2 ln r + C2 r 2 + C3 ln r + C4 .

Этот же результат может быть получен непосредственным интегрированием исходного дифференциального уравнения. Действительно, оператор Лапласа допускает его запись в форме

1 d

d r 2

r d r

d r

Следовательно, само бигармоническое уравнение можно представить в виде

1 d

1 d d

d ϕ

= 0 .

d r

r d r

d r

r d r

Последовательное интегрирование уравнения приводит к тому же виду функции напряжений.

Постоянные интегрирования C1 , C2 , C3 , C4 должны быть найдены из граничных условий в каждой конкретной задаче.

186

Задачи

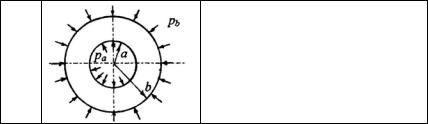
11.1.

Нагружение толстостенного цилиндра равномерным внутренним и внешним давлением (задача Ламе)

Рассматриваемая задача является осесимметричной, поэтому для ее решения можно использовать функцию напряжений в виде:

ϕ = C	1	r2 ln r +C	2	r2	+C ln r +C	4	.
	1		2		3	4

Данной функции напряжений отвечает следующее поле напряжений:

= 1

d ϕ

= C

(1+ 2ln r)+ 2C

r dr

r 2

d 2ϕ

= C

+ 2ln r)+ 2C

−

dr 2

r 2

τrϑ = 0 .

Отметим, что равенство нулю касательных напряжений предопределяется осесимметричностью задачи.

Постоянные интегрирования должны быть определены из граничных условий для напряжений, которые в данной задаче принимают форму:

- при	r = a	σr = −pa	,	τrϑ = 0 ;
- при	r = b	σr = −pb	,	τrϑ = 0 .

Поскольку граничные условия для касательного напряжения τrϑ удовлетво-

ряется тождественно при любых значениях постоянных, имеем всего два уравнения для трех неизвестных. Сложившаяся ситуация показывает, что рассматриваемая задача описывается разрешающим уравнением (относительно функции напряжений ϕ ) меньшего порядка, чем в общем случае. Напомним, что в общем

случае при решении плоской задачи в полярных координатах для определения функции напряжений получили дифференциальное уравнение четвертого порядка.

Выпишем уравнения, определяющие решение осесимметричной задачи: - дифференциальное уравнение равновесия

187

	dσr		+	σr		−σϑ		= 0	;
	d r		+			r		= 0	;
	d r					r
- зависимости Коши
εr =		d u			,		εϑ = u		;
εr =					,		εϑ = u		;
		d r						r
- уравнения линейного физического закона
	εr =		1		(σr −νσϑ) ,
	εr =		E		(σr −νσϑ) ,
			E
	εϑ =		1		(σϑ −νσr ) .
	εϑ =		E		(σϑ −νσr ) .
			E

Построение решения в напряжениях с применением функции напряжений проведем по стандартной схеме.

Получим условие совместности деформаций, исключая перемещение u из зависимостей Коши. Будем иметь

d	(rεϑ)−εr = 0	r	dεϑ	+ εϑ −εr = 0 .
dr
			dr

Подставляя в полученное уравнение значения деформаций в соответствии с линейным физическим законом, получим

r	dσϑ	−rν	dσr	+(1+ν)(σϑ −σr )= 0 .
	dr
			dr

Введение функции напряжений ϕ в предложенном ранее виде

позволяет удовлетворить уравнение равновесия и из преобразованного условия совместности деформаций получить дифференциальное уравнение третьего порядка

d 3 ϕ

1 d 2ϕ

1 d ϕ

1 d

d ϕ

= 0 .

−

= 0

d r

d r r d r

d r

Последовательное интегрирование уравнения позволяет определить функцию

188

напряжений в виде

ϕ = C1 r2 / 4 +C2 ln r +C3

или, в старых обозначениях,

ϕ = C2 r 2 +C3 ln r +C4 .

Получили, что для рассматриваемой задачи постоянная C1 отсутствует, т.е.

C1 = 0 , и из двух граничных условий остается определить постоянные C2 и C3 .

Отметим, что решение поставленной задачи в напряжениях с применением функции напряжений можно свести и к дифференциальному уравнению второго порядка. Действительно, дифференциальное уравнение равновесия можно переписать в виде

d	(rσr )−σϑ = 0	,
d r

что позволяет ввести функцию напряжений в более простой форме:

σr =	ϕ	,	σϑ =	d ϕ	.
	r
				d r

Соответственно, для определения функции напряжений получаем дифференциальное уравнение второго порядка:

d 2ϕ	+	1 d ϕ	−	ϕ	= 0	d	1	d	(rϕ) = 0 .


d r 2		r d r		r 2
						d r r d r

Решение полученного уравнения приводит к несколько иной форме функции напряжений, но напряженное состояние, ей соответствующее, будет тем же самым:

σr =

σr = 2C2

ϕ =

A1 r

r 2

σϑ =

−

σϑ = 2C2

−

r 2

Определение двух постоянных

и C3

из граничных условий приводит к

следующему результату:

189

paa2 − pbb2

C =

( pb − pa ) a2b2

b2 −a2

Если длина цилиндра остается постоянной и деформация εz

равна нулю (ус-

ловие плоской деформации), то имеет место нормальное напряжение σz

σz = ν(σr +σϑ)= 2ν

a2 − p b2

= const ,

b2 −a2

которое приводится к продольной силе

a2 − p b2 ) .

= 2π

∫

rdr = 2πν

Если торцы цилиндра могут свободно смещаться, то в этом случае имеет место деформация εz = const . Величина деформации εz будет определяться из условия

σz = 0 , откуда следует:

	ν	p	a	a2 − p b2
εz = −			a		b	.
εz = −	E			b2	−a2	.
	E			b2	−a2

Если под давлением находится замкнутый цилиндрический сосуд (толстостенная труба с днищами), то продольная сила, определяемая давлениями на днища, будет равна:

N ′z = π (paa2 − pbb2 ) .

Сравнение соотношений для N z и N ′z показывает, что задача о толстостенной трубе с днищами будет задачей о плоской деформации, если материал трубы имеет коэффициент Пуассона ν = 0,5 .

В частном случае, когда давление

равно нулю, соотношения для напряже-

ний принимают вид:

paa

σr =

1−

σϑ =

−a

190

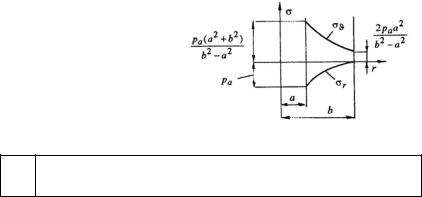
Распределение напряжений по толщине цилиндра для этого случая показано на рис. 11.6. Отметим, что напряжение (σϑ)max по величине всегда больше внутреннего давления pa . Опасные точки

расположены на внутренней

поверхности цилиндра.

Рис. 11.6

1.2. Соединения цилиндров с натягом (соединения цилиндров с использованием горячей посадки или запрессовки)

Предположим, что после соединения с натягом двух цилиндров, изготовленных из разных материалов ( E1 , ν1 и E2 , ν2 ), радиусы внутреннего цилиндра

оказываются равными a и b , а наружного − b и c . Случай a = 0 определяет горячую посадку (запрессовку) цилиндра на вал. Радиальное давление между цилиндрами будем считать равным p .

Если разъединить цилиндры, то внутренний цилиндр будет стремиться расшириться, а наружный – сжаться. Очевидно, что для определения изменения радиусов (для определения радиальных перемещений точек поверхностей цилиндров) необходимо иметь решение задачи о толстостенном цилиндре в перемещениях.

Решение в напряжениях задачи о нагружении толстостенного цилиндра рав-

номерным внутренним pa

и внешним давлением pb имеет вид:

σr

= 2C2 +

σϑ = 2C2 −

r 2

где

a2 − p b2

( p

− p

) a2b2

C =

b2 −a2

Для определения перемещения u = u (r) воспользуемся зависимостями Коши, переписав их с учетом уравнений линейного физического закона. Будем иметь:

d u

(σr −νσϑ)

Eu = 2C2r

(1−ν)−

C3(1+ν)

+C ;

d r

(σϑ −νσr )

Eu =

2C2r (1 −ν)−

C3 (1+ ν)

191

Из сравнения полученных соотношений следует C = 0 , и для описания радиальных перемещений точек цилиндра имеем следующую функцию:

Eu = 2C2r (1 −ν)−	C3 (1+ ν)	.

	r

Теперь используем представленное соотношение для описания расширения

внутреннего цилиндра.	Принимая			pa = 0 , pb = −p и r = b ,	найдем увеличение
его внешнего радиуса. Будем иметь
u1 =		1	pb	[(1+ ν1)a2 + (1 −ν1)b2 ]	,
			b2 − a2
		E1

где E1 , ν1 относятся к материалу внутреннего цилиндра.

Заменив теперь в формулах для постоянных C2 и C3 радиусы a , b , соответственно, на b , c и принимая в этих формулах pa = −p , pb = 0 и r = c , найдем радиальное перемещение точек внутренней поверхности наружного цилиндра:

u2 = −	1	pb	[(1 + ν2 )c2 + (1 − ν2 )b2 ]	,
		c2 −b2
	E2

где E2 , ν2 относятся к материалу наружного цилиндра.

Полученные соотношения для u1 и u2 позволяют определить величину диаметрального натяга δ , при котором радиальное давление между цилиндрами равно p . В частности, если оба цилиндра выполнены из одного и того же материала, будем иметь:

δ	= u1	−u2	=	2b3( c2 − a2 )			p	.
2				( b2	− a2) ( c2	−b2)	E

В случае цилиндра, посаженного на сплошной вал, принимаем a = 0 , и полученная формула преобразуется к виду

δ =	4bc2	p	.
	(c2 −b2)	E

Отметим, что приведенный расчет справедлив в рамках линейной теории упругости.

192

11.3.Напряжения во вращающихся дисках

Будем считать, что напряженное состояние диска при его равномерном вращении полностью определяется центробежными силами. В этом случае задача становится осесимметричной: касательное напряжение τrϑ равно нулю, а нормальные

напряжения σr и σϑ не зависят от переменной ϑ.

Центробежная сила является объемной силой. Соответственно, дифференци-


альное уравнение равновесия принимает вид:
	dσr	+	σr −σϑ +ρω2r = 0				d	(rσr )−σϑ +ρω2r = 0 ,
							d r
	d r		r
где ρω2r − центробежная сила;				ρ	− плотность материала диска: ω − его угло-
вая скорость вращения. Введение функции напряжений ϕ в виде
			σr = ϕ	,	σϑ =	d ϕ		+ ρω2r 2
						d r
			r

позволяет удовлетворить уравнение равновесия.

Исключая перемещение u из зависимостей Коши, будем иметь условие совместности деформаций в уже известном виде:

d	(rεϑ)−εr = 0	r	dεϑ	+ εϑ −εr = 0 .
dr
			dr

Преобразование полученного уравнения с учетом соотношений линейного физического закона и формул, вводящих функцию напряжений, позволяет получить разрешающее уравнение для функции напряжений ϕ :

d	1 d	(rϕ)	= −(3 +ν)ρω2r .
		(rϕ)	= −(3 +ν)ρω2r .

d r r d r

Прямое интегрирование этого уравнения приводит к следующему результату:

σr =

−

3 + ν

ρω2r 2 ,

ϕ =

A1 r

−(3 + ν)ρω

2 r

−

1 + 3ν

σϑ =

−

ρω2r 2 .

r 2

Постоянные интегрирования определим из граничных условий отдельно для сплошного диска и диска с круговым отверстием.

193

Сплошной диск. Поскольку напряжения в центре диска должны быть конечными, следует принять A2 = 0 . Вторая постоянная A1 находится из граничного условия на внешнем радиусе r = b :

σ			= 0	A	=	3 + ν	ρω2b2 .


	r	r =b		1		4

С учетом значений постоянных A1 и A2 соотношения для напряжений принимают вид:

σr =	3 + ν	ρω2 (b2 − r2 ) ,	σϑ =	ρω2	[(3 + ν)b2 −(1 +3 ν)r 2 ] .
	8			8

Оба напряжения имеют равные наибольшие значения в центре диска:

= (σ

)

= σ

= (σ

)

3 + ν

ρω2 b2 .

r =0

max

r =0

ϑ max

Диск с круговым отверстием. Поскольку оба контура ( r = a и r = b ) свободны от внешних сил, граничные условия имеют вид:

откуда следует

σr

r =a = 0 ,

σr

r =b = 0

3 + ν

ρω2 (a2 + b2 ) ,

= −

3 + ν

ρω2a2b2 .

Окружное напряжение σϑ имеет наибольшее значение на внутреннем контуре, где оно равно:

= (σ

)

= 3 + ν

1 − ν

ρω2b2

1 +

r =a

max

3 + ν

Если круговое отверстие в диске мало, так что величиной

(1− ν)a2 / (3 + ν)b2

можно пренебречь по сравнению с единицей, то (σϑ)max

для диска с отверстием

будет в два раза больше, чем для сплошного диска: малое отверстие является концентратором напряжений.

Радиальное напряжение достигает наибольшего значения в точках r = ab .

194

11.4.Напряжения во вращающихся цилиндрах (валах)

Задача о напряжениях во вращающихся цилиндрах (валах) является задачей о плоском деформированном состоянии. Соответственно, если для вращающегося сплошного диска соотношения для напряжений имеют вид:

σr =	3 + ν	ρω2 (b2 − r2 ) ,	σϑ =	ρω2	[(3 + ν)b2 −(1 + 3 ν)r 2 ] ,
	8			8

то для получения таких же соотношений в задаче о вращающемся сплошном вале необходимо вместо действительной упругой постоянной ν ввести фиктивную

упругую постоянную ν = ν/ (1−ν). Будем иметь:

σr

3 + ν

ρω2 (b2 − r2 )

σr =

3 − 2ν

ρω2 (b2 − r2 ) ;

1 − ν

σϑ =

ρω2

[(3 + ν )b2 − (1 + 3ν )r2

] σϑ =

ρω2

[(3 − 2ν)b2 − (1 + 2 ν)r 2

1 − ν

Напомним, что в задаче о плоской деформации напряжение σz = ν(σr +σϑ) отлично от нуля. В задаче о вращающемся сплошном вале для σz получим:

	σz =	νρω2	[(3 − 2ν)b2	− 2r 2 ] .
	σz =	4(1−ν)	[(3 − 2ν)b2	− 2r 2 ] .
		4(1−ν)

11.5.
				Изгиб консоли силой P,
				приложенной на конце

Построим решение с использованием свойств функции напряжений ϕ(x, y).
Будем считать, что для точки A0 (y = −h / 2)				функция напряжений и ее произ-
водная по переменной y равны нулю, т.е.
	A0 (y = −h / 2) :		ϕ = 0 ,	∂ϕ/ ∂y = 0 .

Тогда для точки A(y = h / 2), учитывая, что направление обхода контура балки отрицательное, будем иметь:

195

A(y = h / 2) : ϕ = −P x , ∂ϕ/ ∂y = 0 .

При таких значениях функции напряжений и ее производной по переменной y на контуре естественно пытаться разыскивать саму функцию в виде

ϕ (x, y)= f (y)x .

Подставляя функцию напряжений в бигармоническое уравнение, получим обыкновенное дифференциальное уравнение для функции f (y), решение которо-

го приводит к следующему результату:

x d 4 f = 0 f (y)= a1y3 +a2 y2 +a3y +a4 . d y 4

Постоянные интегрирование должны быть определены из граничных условий, которые для функции f (y) перепишутся в форме:

y = h / 2 :	f = −P ,	d f / dy = 0 ;
y = −h / 2 :	f = 0 ,	d f / dy = 0 .

Подставляя значения функции f (y) и ее производной в представленные соотношения, для определения постоянных получаем следующие уравнения:

+ a2

+ a3

+ a4 = −P

−a1

+ a

−a3

+ a4 = 0

3a1

+ 2a2

+ a3 = 0 ,

3a1

−2a2

+ a3 = 0 .

Из третьего и четвертого уравнений следует, что a2 =

0 , а

= −a1

3h2

. Первые

два уравнения дают a4 = −P / 2

a1 = −2P / h3 ,

что

позволяет

получить

a3 = 3P / 2h .

С учетом найденных значений постоянных функция напряжений принимает вид:

196

	P		3y		4 y		3
ϕ = −		1−		+				x .
						3
2			h		h

11.6.

Клин, нагруженный сосредоточенной силой P, приложенной к его вершине

Построим решение в полярной системе координат с использованием свойств функции напряжений ϕ(r , θ).

Будем считать, что для точки A0 (θ = α) верхней грани клина функция напряжений и ее производная по нормали равны нулю, т.е.

A0 (θ = α): ϕ = 0 ,	∂ϕ	=	∂ϕ	l +	1	∂ϕ	m =	1 ∂ϕ	= 0 .

	∂n							r ∂θ
			∂r		r ∂θ

Здесь учтено, что направляющие косинусы для нормали к верхней грани клина имеют значения l = 0 , m =1 .

Соответственно, для точки A1 (θ = −α) будем иметь:

A (θ = −α):	ϕ = −Pr sin (α + γ) , − 1	∂ϕ	= −Pcos (α + γ) .

1	r ∂θ

Здесь учтено, что направляющие косинусы для нормали к нижней грани клина имеют значения l = 0 , m = −1 .

При таких значениях функции напряжений и ее производной по нормали на контуре естественно пытаться разыскивать саму функцию в виде

ϕ (r , θ)= r f (θ) .

Подставляя функцию напряжений в бигармоническое уравнение, получим обыкновенное дифференциальное уравнение для функции f (θ):

d 4 f	+ 2	d 2 f	+ f	= 0 .
dθ4		dθ2

197

Решение соответствующего характеристического уравнения ( k2 +1) 2 = 0 дает кратные корни k1, 2 = i , k3, 4 = −i , что позволяет записать решение дифференци-

ального уравнения для функции f (θ) в форме:

f (θ)= C1 cosθ+C2 sin θ+C3θcos θ+C4θsin θ .

Постоянные интегрирования могут быть найдены непосредственно из граничных условий, выписанных для функции напряжений на гранях клина при θ = ±α ,

однако возможен и другой путь: определить напряжения по найденной функции напряжений и найти постоянные, удовлетворяя граничные условия в напряжениях.

Рассмотрим второй вариант. Напряженное состояние в данной задаче определяется только двумя постоянными:

	2C		2C	4
σr = −	3	sin θ+		4	cosθ	σr = (Asin θ+ B cos θ)/ r ,
σr = −	r	sin θ+	r		cosθ	σr = (Asin θ+ B cos θ)/ r ,
	σθ = τrθ = 0					σθ = τrθ = 0 .

Граничные условия в напряжениях на гранях клина при θ = ±α принимают

вид

σθ = τrθ = 0 при θ = ±α

и удовлетворяются тождественно при любых значениях постоянных A и B . Однако в рассматриваемой задаче имеют место еще два интегральных граничных условия в вершине клина, позволяющих трактовать приложенную систему распределенных нагрузок как сосредоточенную силу. Эти условия представляют собой условия равновесия части клина, отсеченной дугой радиуса r :

∫σr r dθcos θ = −P cos γ ,

− α

∫σr r d θsin θ = −Psin γ .

− α

Определение постоянных A и B из интегральных граничных условий в вершине клина приводит к следующим результатам:

A = −	Psin γ	,	B = −	2P cos γ	.
	2α −sin 2α			2α +sin 2α

198

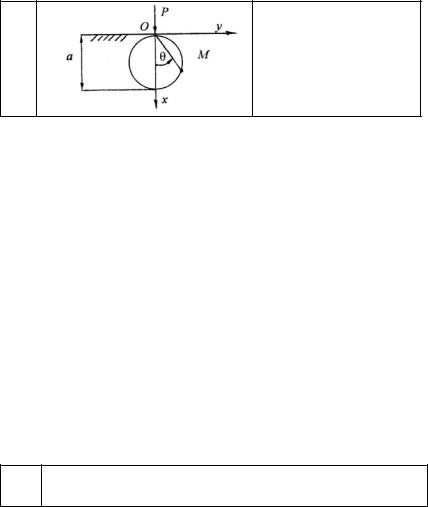
Отметим, что в соответствии с принципом Сен-Венана построенное решение пригодно, начиная с некоторых значений радиуса r (при r → 0 напряжение

σr → ∞ ).

11.7.

Задача о нагружении упругой полуплоскости сосредоточенной силой Р (задача Фламана)

Поставленная задача является частным случаем задачи о клине, нагруженном сосредоточенной силой, приложенной к его вершине. Действительно, если в задаче о клине принять α = π/ 2 и γ = 0 , то получаем задачу Фламана, решение кото-

рой будет иметь вид:

σr = −	2P cosθ	, σθ = τrθ = 0 .
	πr

Характерной особенностью напряженного состояния в рассматриваемой задаче является наличие окружностей равных напряжений: напряжение в любой точке окружности произвольного радиуса a есть величина постоянная. Действительно,

для точки M имеем

σr = −	2P cos θ	= −	2P cos θ	= −	2P	= const .

	π OM		π a cos θ		πa

При исследовании плоского напряженного состояния прозрачных моделей оптическим методом задача Фламана часто используется для демонстрации локального характера напряжений от действия сосредоточенной силы (значения напряжений быстро убывают по мере удаления от точки приложения силы) и подтверждения принципа Сен-Венана (действительное напряжение под силой неопределенно и граничное условие может быть выполнено только интегрально).

11.8. Клин, нагруженный сосредоточенным моментом М, приложенным к его вершине

Решение построим в полярной системе координат с использованием свойств функции напряжений ϕ(r , θ) с обозначениями и по схеме, предложенными при

рассмотрении задачи о клине, нагруженном сосредоточенной силой, приложенной к его вершине.

199

Запишем граничные условия на верхней и нижней гранях клина для функции напряжений и ее производной по нормали. Принимая, что момент M , приложенный к вершине клина, направлен по часовой стрелке, будем иметь:

θ = α :	ϕ = 0	,		∂ϕ		=	1 ∂ϕ		= 0 .

				∂n			r ∂θ

θ = −α :	ϕ = −M ,		∂ϕ		= − 1			∂ϕ	= 0 .

			∂n				r ∂θ

При таких значениях функции напряжений и ее производной по нормали на контуре естественно пытаться разыскивать саму функцию в виде ϕ = ϕ(θ).

Подставляя функцию напряжений в бигармоническое уравнение, получим:

∂

+ 1

∂

1 ∂

∂

= 0

+ 4

= 0 .

∂r

r ∂r

∂θ

Решение соответствующего характеристического уравнения

k 2 (k 2 + 4)= 0 да-

ет корни k1, 2 = 0 , k 3 = 2i ,

k 4 = −2i , что позволяет записать решение дифферен-

циального уравнения для функции напряжений в форме:

ϕ(θ)= C1 +C2θ+C3 cos 2θ+C4 sin 2θ .

Напряженное состояние в данной задаче определяется соотношениями:

= −

(C cos2θ+C

sin 2θ)

σθ = 0 ,

rθ

−2C sin 2θ+2C

cos2θ) .

Граничные условия в напряжениях на гранях клина принимают вид

σθ = τrθ = 0

при

θ = ±α

и удовлетворяются при

C3 = 0

и C2 = −2C4 cos 2α ,

что позволяет переписать

соотношения для напряжений в виде:

σr = −

4C4

sin 2θ

σr

= −

sin 2θ

200

τrθ =	2C4	(cos2θ−cos2α)	τrθ =	A	(cos2θ−cos2α) .
	r2			r2

Однако в рассматриваемой задаче имеет место еще одно интегральное граничное условие в вершине клина (условие равновесия части клина, отсеченной дугой радиуса r ), позволяющее трактовать приложенную систему распределенных нагрузок как сосредоточенный момент (принцип Сен-Венана). Применение этого условия для определения постоянной A дает:

α	α		M
∫τrθ (r dθ)r = M	A ∫ (cos 2θ−cos 2α)dθ	A =	M		.
∫τrθ (r dθ)r = M	A ∫ (cos 2θ−cos 2α)dθ	A =	sin 2α −2αcos 2α		.
−α	−α		sin 2α −2αcos 2α
−α	−α

11.9.		Растяжение		полосы
		Растяжение		полосы
		с круговым отверстием
		(задача Кирша)

При растяжении полосы, не имеющей отверстия, ее напряженное состояние можно записать в виде:

σ0x = S , σ0y = τ0xy = 0 ,

что соответствует следующей функции напряжений:

ϕ0 = S y2 / 2 .

Поскольку в задаче предполагается наличие кругового отверстия, в дальнейшем будем использовать полярную систему координат. Соответственно, в полярной системе координат напряженное состояние полосы без отверстия будет определяться соотношениями:

ϕ0 = Sr 2 sin 2 θ/ 2		ϕ0 = S r2 (1−cos 2θ)/ 4 ;
σ0r = S (1+cos 2θ)/ 2			,
σ0	= S (1−cos 2θ)/ 2		,
θ
τ0		= −(S / 2)sin 2θ .
rθ

Если же в растянутой сплошной полосе сделать отверстие, то, очевидно, что

201

напряжения, вызванные наличием отверстия, будут иметь локальный характер, а на достаточно большом расстоянии от отверстия напряжения будут такими же, как и в сплошной полосе. Исходя из этих соображений, в поставленной задаче функцию напряжений будем разыскивать в форме:

ϕ = f1(r)+ f2 (r)cos 2θ ,

выполняя следующие граничные условия:

- при r = a :	σr = τrθ = 0		;
- при r → ∞ :	σr = σ0r	,	σθ = σθ0 , τrθ = τ0rθ .
Для отыскания функций		f1(r) и f2 (r) подставим функцию напряжений ϕ в

бигармоническое уравнение. Поскольку полученное уравнение должно удовлетворяться при любых значениях угла θ, оно распадается на два отдельных дифференциальных уравнения относительно f1(r) и f2 (r):

d 2

1 d

d 2 f

1 d f

= 0

dr2

r dr

dr2

r dr

d f2

4 f2

−

= 0 .

r dr

Первое из полученных уравнений уже рассматривалось при рассмотрении плоской осесимметричной задачи, и его общее решение имеет вид:

f (r)= C	1	r2 ln r +C	2	r2	+C ln r +C	4	.
1	1		2		3	4

Раскрывая второе уравнение, будем иметь:

d 4 f2

d 3 f2

−

d 2 f2

df2

= 0 .

dr 4

r dr3

r 2

dr 2

r3 dr

C применением подстановки t = ln r

уравнение относительно функции f2 (r)

приводится к обыкновенному дифференциальному уравнению с постоянными коэффициентами

d 4 f2	−4	d 3 f2	−4	d 2 f2	+16	d f2	= 0 .
d t 4		d t3		d t 2		d t

202

Рассмотрение соответствующего характеристического уравнения позволяет

определить его корни ( k1 = 0 , k2 = 4 ,

k3 = 2 ,

k4 = −2 ) и записать решение диф-

ференциального уравнения относительно функции

f2 (r) в форме:

(t)= C e2t +C

e4t +C

e−2t +C

(r)= C

r 2 +C

r −2 +C .

Таким образом, с учетом найденных функций

f1(r) и

f2 (r)

функция напря-

жений принимает вид:

ϕ(r , θ)= C1 r2 ln r +C2 r2 +C3 ln r +C4 + (C5r2 + C6r4 + C7r−2 + C8 )cos 2θ .

Значения постоянных, входящих в решение, должны быть найдены из граничных условий в напряжениях.

Выпишем соотношения, определяющие напряженное состояние в данной задаче. Будем иметь:

1 ∂

∂ϕ

= C1(1

+ 2ln r)

6C7

4C8

+ 2C2 +

2C5

σr =

−

cos 2θ ,

r2 ∂θ2

∂r

r 4

r 2

∂

= C1(3 + 2ln r)+ 2C2 −

6C7

σϑ =

2C5

+12C6r

cos 2θ ,

∂r

∂

∂ϕ

6C7

2C8

−

2C5 +6C6r

τrθ =

−

sin 2θ .

∂r∂θ

∂θ

r 4

r 2

Поскольку напряжения должны быть конечными при r → ∞ , необходимо потребовать, чтобы постоянные C1 и C6 были равны нулю ( C1 = C6 = 0 ). Для определения остальных пяти постоянных имеем пять уравнений, следующих из граничных условий:

σr (a)= 0

6C7

4C8

2C2

2C5

−

cos 2θ = 0 ,

(a)= 0

6C7

2C8

rθ

−

sin 2θ = 0

σr (∞)= σ0r

2C2 −2C5 cos 2θ = S (1+cos 2θ)/ 2

σθ(∞)= σθ0

2C2 +2C5 cos 2θ = S (1−cos 2θ)/ 2

rθ

(∞)= τ0

sin 2θ = −(S / 2)sin 2θ .

rθ

203

Из последнего пятого уравнения следует C5 = −S / 4 . Третье и четвертое уравнения являются линейно зависимыми и позволяют определить только одну постоянную C2 =S / 4 . Первое и второе уравнения должны удовлетворяться при любых значениях переменной θ, и поэтому распадаются на три уравнения:

2C2 +

= 0

2C5

6C7

4C8

= 0 ,

a 4

2C5

−

6C7

−

2C8

= 0 .

Решением полученных уравнений будут следующие значения оставшихся постоянных:

C = −Sa2	/ 2 ,	C =Sa2	/ 2 ,	C	7	= −Sa4	/ 4 .
3		8			7

Подставляя значения найденных постоянных в соотношения для напряжений, будем иметь:

σr

1−

+ 3a4

−

4a2

cos 2θ

r 2

r 4

r 2

σθ =

−

cos 2θ

τrθ =

−

1− 3a

sin 2θ .

Покажем распределение напряжений по контуру

кругового отверстия (рис. 11.7). Напряжения в точках

контура определяются соотношениями:

σθ (a, θ)

= S (1 − 2 cos 2θ)

σr = τrθ = 0 .

Рис. 11.7

Приведенная

эпюра σθ (a, θ) показывает, что в

точках 1

контура

отверстия ( θ = 0 ) имеют место

напряжения сжатия

σθ = −S , а в точках 2 ( θ = π/ 2 ) – напряжения растяжения

σθ = 3S .

204

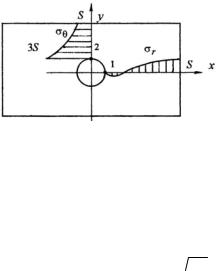
Характер изменения напряжения σθ по мере удаления от кон-

тура отверстия вдоль оси y (от

точки 2) проследим, построив эпюру по соотношению:

3a4

σθ r ,

2 +

Рис. 11.8

Построенная эпюра σθ (r , π/ 2) показывает локальный характер влияния от-

верстия на распределение напряжений в полосе (рис.11.8). Действительно, с увеличением расстояния r от точки 2 величина напряжения σθ быстро уменьшает-

ся от значения 3S , так что на расстоянии примерно пяти радиусов она практически не отличается от S . Отметим, что расстояние, равное пяти радиусам, можно рассматривать как бесконечно большое, поскольку в этом случае напряженное состояние полосы не будет отличаться от напряженного состояния плоскости.

Построение эпюры напряжений σr (r , 0) показывает, что в точке r = 6 / 5 a имеет место сжимающее напряжение σr = − S / 24 .

Рассмотренная задача (задача Кирша) является характерным примером влияния концентратора напряжений (в данном случае – малого кругового отверстия), наличие которого приводит к значительным локальным (местным) напряжениям, быстро затухающим по мере удаления от него. Обычно локальные напряжения характеризуют коэффициентом концентрации напряжений k , представляющим собой отношение наибольшего местного напряжения к номинальному напряжению, вычисленному в предположении, что концентратор отсутствует. В рассматриваемом случае k = 3S / S = 3 . Отметим, что наличие концентраторов напряжений ведет не только к повышению напряжений вблизи них, но и к изменению характера напряженного состояния элемента конструкции.

Представленное выше решение задачи Кирша позволяет легко получить решение задачи о растяжении пластины с малым круговым отверстием в двух взаимно перпендикулярных направлениях.

Построение решения покажем на примере напряжения σr . При растяжении пластины усилиями S в направлении оси x для напряжения σr получили:

σr =

1−

−

cos 2θ .

При растяжении пластины усилиями S

в направлении оси

y напряжение σr

будет определяться этой же формулой,

но с заменой угла θ

на угол θ+(π/ 2).

Суммирование напряжений в соответствии с принципом суперпозиции приводит к

205

соотношению:

		a	2
σr = S	1−			,

		r	2

Так же легко можно построить решение задачи о растяжении пластины усилиями S в направлении оси x и сжатии усилиями ( −S ) в направлении оси y .

11.10. Тонкий круговой диск при неравномерном распределении температуры.

Рассмотрим частный случай, когда температура является функцией только радиуса r , т.е. случай осесимметричного плоского напряженного состояния.

Основные уравнения, определяющие поставленную задачу, имеют вид: - дифференциальное уравнение равновесия

	dσr			+		σr		−σϑ	= 0	;
	d r							r

- зависимости Коши
εr =			d u				,	εϑ	= u	;

				d r					r
- уравнения линейного физического закона
εr =		1			(σr −νσϑ)+αT ,
		E

εϑ =		1			(	σϑ −νσr )+αT .
		E

Представление дифференциального уравнения равновесия в форме

ddr (rσr )−σϑ = 0

позволяет ввести функцию напряжений ϕ в следующем виде:

σr =	ϕ	,	σϑ =	d ϕ	.
	r
				d r

206

Условие совместности деформаций получим, исключая перемещение u из зависимостей Коши. Будем иметь:

d	(rεϑ)−εr = 0	r	d εϑ	+ εϑ − εr = 0 .
dr
			dr

Преобразование полученного уравнения с учетом соотношений линейного физического закона и формул, вводящих функцию напряжений, позволяет получить для функции напряжений ϕ дифференциальное уравнение второго порядка:

d 2ϕ

1 d ϕ

−

= −αE

(rϕ) = −αE

d r2

r d r

d r r d r

Последняя запись дифференциального уравнения, определяющего функцию напряжений, позволяет непосредственное интегрирование. Будем иметь:

	αE	r	C r		C	2
ϕ = −	r	∫T (r)rdr +	1	+			.
			2
		a			r

Для диска с центральным отверстием нижний предел интегрирования a соответствует значению внутреннего радиуса, для сплошного диска должны принять a = 0 .

По известным формулам определим напряжения. Получим:

αE

T (r)rdr +

σr =

= −

∫

r 2

dϕ

T (r)r dr −T

σθ =

= αE

∫

−

Постоянные интегрирования определим отдельно для диска с отверстием и сплошного диска.

Диск с отверстием. Граничные условия в данной задаче имеют вид:

σr

r =a

= 0

= 0 ,

αE b

σr

r =b = 0

∫ T (r)r dr .

Решение уравнений относительно постоянных C1 и C2 позволяет получить:

207

		αa2E	b	C		α E	b
C2	= −		∫ T (r)r dr ,	1	= −		∫ T (r)rdr .
C2	= −	b2 −a2	∫ T (r)r dr ,	2	= −	b2 −a2	∫ T (r)rdr .
		b2 −a2	a	2		b2 −a2	a

Подставим полученные значения постоянных в соотношения для напряжений. После некоторых преобразований будем иметь:

−a

σr =

α E

∫T (r)rdr − ∫

T (r)rdr

−a

α E

T (r)rdr +

T (r)rdr −T (r)r2

σθ =

∫

−a

В частном случае T = const получим ожидаемый результат: σr = σθ = 0 .

Сплошной диск. Соотношения, определяющие напряжения в сплошном диске, легко получить, положив a = 0 в формулах для напряжений в диске с отверстием. В этом случае имеем:

			1		b					1		r
σr = α E					∫ T (r)rdr −							∫	T (r)rdr	,
				2							2
					0				r			0
		b
			b			1		r
σθ = α E	1		∫	T (r)rdr +				∫			T (r)rdr −T (r) .
							2
		2				r
b			0					0

Этот же результат получим, если постоянные C1 и C2 будем определять непосредственно для сплошного диска, принимая C2 = 0 (напряжения в центре диска должны быть конечными) и выполняя граничное условие σr r =b = 0 .

Обратим внимание на необходимость дополнительного исследования соотношений для напряжений, поскольку напряжения σr и σθ сохраняют неопределен-

ность при r → 0 за счет второго слагаемого. Раскрывая эту неопределенность, будем иметь:

∫ T (r)rdr

T (r)r

T (0)

T (r)rdr =

lim

0∫

lim

= lim

lim

(r 2 )

r→0 r 2

r→0

r →0

Легко видеть, что упомянутая неопределенность – кажущаяся, поскольку температура в центре диска всегда конечна.

208

Рис. 12.1

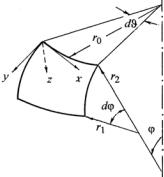
12. Осесимметричное нагружение оболочек вращения

В теории упругости оболочкой называют тело, заключенное между двумя криволинейными поверхностями, расстояние между которыми, именуемое в дальнейшем толщиной оболочки h , мало по сравнению с прочими его размерами. Вообще говоря, толщина оболочки может быть переменной величиной, однако среди реальных конструкций в подавляющем большинстве встречаются оболочки, толщина которых постоянна. В дальнейшем будем рассматривать именно такие оболочки.

Поверхность, делящую толщину оболочки пополам, называют срединной поверхностью. Геометрия оболочки будет полностью определена, если задана форма срединной поверхности и толщина оболочки.

В зависимости от толщины оболочки делятся на тонкие и толстые. К тонким оболочкам, которые и будем рассматривать в дальнейшем, обычно относят такие, у которых отношение толщины h и минимального радиуса кривизны R определяется значением h / R ≤1/10 . Следует отметить, что это значение имеет условноориентировочный характер.

Наиболее важный случай оболочек – оболочки вращения, срединная поверхность которых образуется от вращения плоской кривой вокруг оси, лежащей в ее плоскости и не пересекающей эту кривую.

Для оболочки вращения положение произвольной точки на срединной поверхности определяется пересечением меридиана и параллели (рис. 12.1). В качестве криволинейных координат удобно выбрать углы ϑ и ϕ. Угол ϑ лежит в плоскости

параллели и отсчитывается от некоторой заданной меридианной плоскости. Угол ϕ образуется направлением

нормали к срединной поверхности и

209

осью вращения. Положительная координата z отсчитывается по внутренней нормали к срединной поверхности в рассматриваемой точке. Соответственно, элемент срединной поверхности оболочки вращения вырезается двумя меридианными плоскостями, проходящими через ось вращения, и двумя коническими поверхностями, перпендикулярными к меридианным плоскостям.

Прямоугольную систему координат обычно вводят следующим образом: ось x направляют по касательной к параллельному кругу, ось y − по касательной к меридиану, а ось z оставляют нормаль-

ной к срединной поверхности.

Меридианная плоскость и коническая поверхность, перпендикулярная к ней, определяют плоскости главных радиусов кривизны r1 и r2 в некоторой точке срединной поверхности оболочки. Ради-

ус параллельного круга обозначим через r0 . Длины встречающих-

ся в точке M сторон выделенного элемента срединной поверхности будут равны r1 dϕ и r0 dϑ или r2 sin ϕdϑ.

12.1.Безмоментная теория осесимметрично нагруженных оболочек вращения

При расчетах на прочность тонких оболочек используются различные теории. Самой простой из них является безмоментная теория оболочек. Безмоментная теория строится на основе допущения, что при расчете оболочки можно пренебречь изгибающими моментами и перерезывающими силами, действующими в нормальных сечениях, и, соответственно, связанными с ними напряжениями, принимая во внимание только лишь напряжения растяжения, обусловленные деформацией срединной поверхности оболочки. При этом срединная поверхность подвергается равномерной деформации, а так как толщина оболочки мала, можно считать, что растягивающие напряжения распределены по толщине равномерно. При таком упрощении задача об определении напряжений в оболочке становится статически определимой и легко решается.

Условия применимости безмоментной теории для расчета тонких оболочек формулируются в виде следующих критериев безмоментности напряженного состояния:

210

-края оболочки должны быть свободны от изгибающих моментов и перерезывающих сил, а их повороты и нормальные прогибы не должны быть стеснены;

-радиусы кривизны, граничный контур, толщина оболочки, компоненты поверхностной и краевой нагрузок должны быть плавными функциями.

При составлении уравнений равновесия элемента оболочки вращения примем во внимание, что в теории тонких пластин и оболочек принято оперировать не напряжениями, а результирующими силами и моментами, отнесенными к единице длины сечения.

Безмоментное напряженное состояние в оболочке реализуется,

если	известны	меридиональное
N1 ,	окружное	N2 и сдвигающее

S усилия (рис. 12.2). Поскольку в безмоментной теории полагается, что напряжения распределяются по толщине равномерно, связь между напряжениями и рассматриваемыми усилиями определится соотношениями:

N1 = σm h , N2 = σt h ,

Рис. 12.2

S = τh .

Будем полагать, что произвольная внешняя нагрузка, отнесенная к единице площади срединной поверхности и имеющая составляющие qx , qy , qz по координатным осям xyz , непрерывно рас-

пределена по поверхности оболочки.

Выполнение условий равновесия элемента оболочки вращения приводит к трем дифференциальным уравнениям (два уравнения сил и уравнение моментов) относительно определяемых усилий N1 , N2 и S . Соответствие числа уравнений числу неизвестных

указывает на то, что задача определения усилий в безмоментной оболочке является статически определимой.

Если нагрузка, приложенная к оболочке вращения осесиммет211

рична (симметрична относительно оси вращения), то разрешающие уравнения безмоментной теории существенно упрощаются.

Не останавливаясь на процедуре получения уравнений равновесия элемента оболочки вращения и на их последующих математических преобразованиях, приведем эти уравнения при осесимметричном нагружении оболочки в готовом виде. Будем иметь:


N1	+	N2	= qz σm +		σt	=	p	(уравнение Лапласа),
							h
r1		r2		r1	r2
		2πr0N1 sin ϕ = P				2πr0σmh sin ϕ = P .

Здесь q z = p − внутреннее давление, являющееся функцией коор-

динаты, отсчитываемой вдоль оси вращения; P − равнодействующая всей внешней нагрузки, приложенной к части оболочки, определяемой углом ϕ.

Широкое использование безмоментной теории оболочек объясняется не только относительной простотой ее математического аппарата, но и тем, что она вполне удовлетворительно описывает работу различных конструкций, реализованных в форме тонких оболочек, при достаточно широком классе внешних воздействий.

Безмоментное напряженное состояние является технически наиболее выгодным вследствие равномерности работы материала оболочки. Поэтому сформулированные выше условия применимости безмоментной теории следует рассматривать как «прочностные» рекомендации при проектировании тонкостенных конструкций. Конечно, не всегда они могут быть выполнены либо в силу назначения конструкции, либо в силу других соображений (технология, габариты, экономика), но они являются тем «идеалом», к которому следует стремиться. Обычно конструкционными решениями удается добиться работы основной части оболочки в безмоментном напряженном состоянии, локализуя моментное напряженное состояние в зоне, примыкающей к краю оболочки (краевой эффект). Для расчета краевого эффекта необходимо использовать моментную теорию тонких оболочек, построение которой проведем для симметрично нагруженных оболочек вращения.

212

12.2. Моментная теория осесимметрично нагруженных оболочек вращения

Из	осевой		симметрии
задачи следует, что по сто-
ронам	элемента		оболочки,
расположенным			в	мери-
диональных		плоскостях,
будут	действовать			только
нормальные		напряжения,
которые сводятся к резуль-
тирующей силе N2 r1d ϕ и
результирующему моменту
M 2 r1d ϕ, причем и сила, и					Рис. 12.3

момент	не	будут зависеть от угла ϑ, определяющего положение
меридианов (рис. 12.3).

На сторонах элемента оболочки, перпендикулярных к меридианам и определяемых углом ϕ, также будут действовать нормаль-

ные напряжения, сводящиеся к результирующей силе N1r2 sinϕdϑ и результирующему моменту M1r2 sin ϕd ϑ. Из касательных на-

пряжений на этих сторонах останутся (из-за осесимметричности оболочки и нагрузки) только такие, которые сводятся к результирующей силе Q1r2 sinϕdϑ, направленной по нормали к срединной

поверхности оболочки. С изменением угла ϕ значения N1 , M1 и Q1 могут меняться.

Будем полагать, что произвольная внешняя нагрузка имеет составляющие qy и qz .

Рассмотрение равновесия элемента оболочки, находящегося под действием всех приложенных нагрузок, показывает, что три уравнения равновесия будет удовлетворяться тождественно, а оставшиеся три (два уравнения сил относительно осей y и z и уравне-

ние моментов относительно оси x ) принимают следующий вид:

213

(N r

)− N

cos ϕ−

r0Q1

+ r q

= 0

dϕ

1 0

+ N

sin ϕ+

(r Q

)+ r q

= 0

dϕ

0 1

(M r )− M

cos ϕ− r Q = 0 .

dϕ

1 0

0 1

В представленные три уравнения равновесия входят пять неизвестных величин (три силы и два момента), однако перерезывающая сила Q1 может быть исключена из рассмотрения с использо-

ванием третьего уравнения. Тем не менее задача остается статически неопределимой, т.е. полученной системы уравнений недостаточно, и для решения задачи необходимо привлекать зависимости Коши и уравнения линейного физического закона.

Зависимости Коши, полученные для представления деформаций произвольного трехмерного упругого тела в криволинейной системе координат, довольно громоздки, и пользоваться ими трудно. Однако возможно построение упрощенной (технической или прикладной) моментной теории осесимметрично нагруженных тонких оболочек вращения за счет введения следующих допущений (гипотез Кирхгофа – Лява), учитывающих особенности поведения рассматриваемых оболочек под нагрузкой:

-прямолинейный элемент, нормальный к срединной поверхности до деформации, остается прямолинейным и нормальным к деформированной срединной поверхности;

-нормальные напряжения на площадках, параллельных срединной поверхности, пренебрежимо малы по сравнению с прочими напряжениями.

Введение указанных допущений дает возможность пренебречь деформациями сдвига в плоскостях нормальных сечений и линейной деформацией в направлении толщины оболочки. Кроме того, принимая во внимание осесимметричность задачи, дополнительно будем иметь, что перемещение v в окружном направлении равно нулю. Окончательно, связь между деформациями и перемещениями (зависимости Коши) в рассматриваемой задаче принимают вид:

214

ε1 = ε10 − zκ1 ,

ε2 = ε20 − zκ2

где введены следующие обозначения:

∂u

ε10 = r

∂ϕ

ε20 = r

cosϕ −

− w0

∂

1 ∂w0

cos ϕ

∂w0

κ =

∂ϕ

r r

∂ϕ

0 1

В приведенных соотношениях ε1 , ε2

− деформации произволь-

ных элементов оболочки; ε10 ,

ε20

− деформации элементов сре-

динной поверхности оболочки;

κ1 , κ2

− изменения кривизны в

меридианном и перпендикулярном ему направлениях;

u0 , v0 −

перемещения точек срединной поверхности.

Напряженное и деформированное состояния оболочки связаны уравнениями линейного физического закона:

σ =			E	(ε +νε		)	,	σ		=		E	(ε		+ νε ) .
1	1		−ν2	1	2				2	1		−ν2		2	1

Переходя от напряжений к усилиям и моментам, получим следующие соотношения:

N		=		Eh	(ε		+ νε		)	,
			1 −ν2
	1					10		20
N		=		Eh	(ε		+νε		)	,
			1−ν2
	2					20	10
	M 1 = −D (κ1 + νκ2 )									,
	M 2 = −D (κ2 + νκ1) ,
					215

где D = Eh3 /12 (1−ν2 )− цилиндрическая жесткость оболочки. Таким образом, к двум уравнениям равновесия с четырьмя неиз-

вестными N1 , M1 и N 2 , M 2 добавили четыре уравнения для этих усилий и моментов с четырьмя неизвестными деформациями

срединной	поверхности оболочки и изменениями кривизн
( ε10 , ε20 ,	κ1 , κ2 ) и четыре уравнения, связывающие деформации

срединной поверхности оболочки и изменения кривизн с перемещениями точек срединной поверхности (еще две неизвестные u0 , v0 ). Тем самым, имеем полную систему уравнений для оты-

скания всех неизвестных величин, определяющих решение поставленной задачи. В дальнейшем при рассмотрении подобных систем уравнений индекс "0", определяющий величины, относящиеся к

срединной поверхности оболочки, будем опускать.

12.2.1. Круговая цилиндрическая оболочка при осесимметричном нагружении

Для круговой цилиндрической оболочки постоянной толщины, нагруженной симметрично относительно оси, систему определяющих уравнений и их решение можно существенно упростить.

Выберем координатную систему так, чтобы координата x отсчитывалась вдоль образующей, ϕ − в окружном направлении, а

z− вдоль нормали к срединной поверхности оболочки (рис. 12.4). Радиус цилиндра считаем равным a .

Рис. 12.4

216

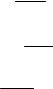
Нагружение цилиндра реализуем приложением только поперечной нагрузки q z = p ( q y = 0 ) – давления, нормального к сре-

динной поверхности оболочки.

Для получения определяющих уравнений в рассматриваемом случае воспользуемся соответствующими уравнениями, записанными для осесимметрично нагруженных оболочек вращения, переходя к принятым здесь обозначениям (индексы "1" и "2" заменяя

на индексы "x" и "ϕ") и учитывая, что 1/ r1 = 0 , r2 = a , ϕ = π/ 2 и r1d ϕ dx .

С учетом всего сказанного дифференциальные уравнения равновесия принимают вид:

d Nx = 0 , d x

Nϕ + a ddQxx + ap = 0 ,

d M x −Qx = 0 . d x

Соответственно, уравнения, связывающие деформации и изменения кривизн, приводятся к виду:

εx	=	du	,	εϕ = − w			,
		d x
						a
κ	=	d 2 w	,	κ	2	= 0 .

1		d x2

Переходя к усилиям и моментам, получим следующие соотношения:

−ν

− w

+ ν

−ν

217

	M x = −D	d 2w
		dx2

M ϕ = −D ν d 2w dx2

Qx =	dM x	= −D	d 3w	,
	dx		d x3

M ϕ =νM x .

Первое из дифференциальных уравнений равновесия показывает, что в рассматриваемой задаче продольные усилия Nx , определяющие растяжение оболочки, постоянны. В дальнейшем будем полагать, что они равны нулю ( N x = 0 ). Если же возникает необходимость учесть их отличие от нуля, то деформации и напряжения, обусловленные этими усилиями, могут быть вычислены отдельно и суммированы с деформациями и напряжениями, вызванными поперечной нагрузкой p . С другой стороны, приняв N x = 0 ,

из соотношения для усилия N x		находим:
	du	= ν	w	,
	dx		a

что, в свою очередь, позволяет записать соотношение для усилия Nϕ в виде:

Nϕ = −	Eh w	.

	a

Возвращаясь к дифференциальным уравнениям равновесия, можно видеть, что второе и третье уравнения сводятся к одному:

d 2M x	+	1	Nϕ = −p .
d x2		a

Подставляя в полученное уравнение соотношения для Nϕ и M x , приходим к обыкновенному дифференциальному уравнению

218

четвертого порядка с постоянными коэффициентами:

D	d 4w	+	Eh	w = p	d 4w	+ 4β4w = p / D ,
	dx4				dx4
			a2

где введено обозначение β4 = Eh / 4a2D = 3(1−ν2 )/ a2h2 .

Таким образом, получили, что решение задачи о круговой цилиндрической оболочке постоянной толщины, нагруженной симметрично относительно оси, сводится к интегрированию неоднородного дифференциального уравнения прогибов.

Общее решение соответствующего однородного уравнения будет иметь вид:

w = eβx (C cosβx +C		2	sin βx)+e−βx (C cosβx +C		4	sin βx) .
1				3
Отметим, что	соотношение типа			C1 cos βx +C2 sin βx можно

представить в виде Acos (βx + θ) , где A и θ − постоянные. Общее решение неоднородного уравнения запишем в форме:

w = w + w1 ,

где w1 − частное решение неоднородного дифференциального уравнения прогибов, определяемое характером распределения нагрузки p . В частности, при p = const имеем, что w1 = pa2 / Eh .

Четыре постоянные интегрирования C1 , C2 , C3 , C4 должны

быть найдены из четырех граничных условий на концах (краях) оболочки (по два условия на каждом краю).

Представим наиболее часто встречающиеся граничные условия на краю оболочки:

- край оболочки жестко закреплен (заделан)

w = 0 ,	d w	= 0 ;
w = 0 ,	dx	= 0 ;
	dx
219

- край оболочки шарнирно оперт

w = 0 , M x = 0 d 2w / dx2 = 0 ;

- край оболочки свободен

M x = 0 d 2w / dx2 = 0 ,

Q	x	= 0	Q	= −D	d3w	d3w	= 0 ;
	x		x		d x3	d x3
					d x3	d x3

- край оболочки нагружен силой Q0 и моментом M 0

D	d 2w	= M0 , − D	d 3w	= Q0 .
	dx2		d x3

Задачи

12.1.

Считая емкость невесомой, определить напряжения в ее сечениях.

По условию задачи собственным весом оболочки пренебрегаем и, соответственно, реакция опоры равна нулю.

Для решения задачи используем безмоментную теорию осесимметрично нагруженных оболочек вращения.

Нормальные напряжения σm и σt будем определять, рассекая оболочку в ее сферической, цилиндрической и конической частях.

Сферическая часть.

	Условие равновесия рассматриваемой отсе-
	ченной части оболочки (рис.12.5) имеет вид:
	(σm 2πr δ)sin ϕ = p0 πr 2 .
Рис. 12.5	Учитывая, что r = R sin ϕ, и решая уравнение
	220

относительно напряжения σm , получим:

σm = p0R / 2δ .

Для определения σt используем уравнение Лапласа при ρm = ρt = R и найденном значении σm . Будем иметь:

σt = p0R / 2δ .

Цилиндрическая часть.

Условие равновесия оставленной части оболочки (рис.12.6) запишем в форме

σm 2πR δ = p0 πR2	,
откуда находим:	Рис. 12.6

σm = p0R / 2δ .

Из уравнения Лапласа при ρm = ∞ , ρt = R получаем:

σt = p0R / δ .

Коническая часть.

Условие равновесия оставленной части оболочки (рис.12.7) имеет вид:

	(σ	m	2πrδ)cos α = πr2 p .
		m	0
Определяя	из		уравнения напряжение σm	и
учитывая,	что r = ztgα (0 ≤ z ≤ R) , получим			Рис. 12.7

σm = p0 ztgα/ 2δcos α .

Решая уравнение Лапласа относительно σt при ρm = ∞ , ρt = r / cosα , будем иметь:

σt = p0 ztgα/ δcos α .

221

Результаты определения напряжений в сечениях рассматриваемого резервуара
сведем в табл. 12.1.
					Таблица 12.1
Напряжения	Сфера	Цилиндр	Конус
Напряжения	Сфера	Цилиндр	напряжения		наибольшие
			в произвольном сечении		напряжения
σm	p0 R / 2δ	p0 R / 2δ	p0 z tgα / 2δcos α		p0 R /	2 δ
σt	p0 R / 2δ	p0 R / δ	p0 z tgα / δcos α		2 p0 R / δ
Опасным является сечение в конической части резервуара при					z = R . Напря-
женное состояние − двухосное: σ1 =			2 p0 R / δ , σ2 = p0R /	2 δ ,	σ3 = 0 .

12.2.	Изгиб	длинной цилиндри-
	ческой оболочки, жестко за-
	крепленной по краю, нагру-
	женной	равномерным внут-
	ренним давлением р

Напомним, что решение задачи о круговой цилиндрической оболочке постоянной толщины h , нагруженной симметрично относительно оси, сводится к интегрированию неоднородного дифференциального уравнения прогибов, решение которого в данном случае принимает форму:

w = e−βx (C	cosβx +C	4	sin βx) −	pa2	.

3				Eh

Здесь принято во внимание, что для больших значений переменной x (оболочка длинная) прогиб должен быть конечным ( C1 = C2 = 0 ), а частное решение неоднородного дифференциального уравнения прогибов, определяемое внутрен-

ним давлением p , имеет вид w1 = −pa2 / Eh .

Край оболочки жестко закреплен (заделан). Соответственно, постоянные C3 и C4 должны быть найдены из следующих граничных условий:

Решение соответствующих уравнений относительно C3 и C4 позволяет полу-

чить:

222

C3 = C4 = pa2 / Eh .

Таким образом, прогиб оболочки определяется соотношением

w =	pa2	[e−βx (cosβx +sin βx)−1 ] .
	Eh

С увеличением переменной x значение прогиба стремится к величине δ = pa2 / Eh , что соответствует изменению (увеличению) длины радиуса при свободных торцах оболочки. Действительно, в соответствии с соотношениями безмоментной теории имеем: σϕ = pa / h , δ/ a = σϕ / E δ = pa2 / Eh (знак « − » для перемещения w показывает, что оно направлено обратно положительному направлению оси z ). Данное обстоятельство подчеркивает локальный характер полученного решения и позволяет провести оценку протяженности зоны краевого эффекта или, другими словами, определить длину оболочки, при которой взаимным влиянием краев можно пренебречь. В этом случае оболочку можно считать длинной. Общепринятыми являются следующие оценки:

- если приемлема 10 % -ная погрешность расчета, то оболочку можно считать

ν =0,3	Rh ( L , R , h − длина, радиус и тол-
длинной при βL > 2 → L >1,5	Rh ( L , R , h − длина, радиус и тол-
щина оболочки);

- если приемлема 5 % -ная погрешность расчета, то оболочку можно считать

ν =0,3	Rh .
длинной при βL > 3 → L > 2,35

Вычисление изгибающего момента M x и пе-

ререзывающей силы Qx в закреплении (рис.12.8) позволяет получить:

Рис. 12.8

M x = −D

d 2w

M x

= M

;

dx2

x=0

2β2

= D

d3w

= Q

= −

d x3

x=0

Определение наибольших напряжений изгиба (σx )max в закреплении приводит к следующему результату:

223

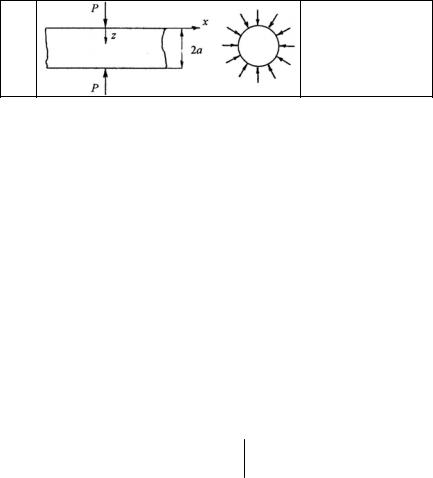
	12M x		(σx )max =	12M0		h	ν =0,3	pa
σx =		z					→ (σx )max = 3,63		.
σx =	h3	z		h3	2		→ (σx )max = 3,63	2h	.
	h3			h3	2			2h

Полученное значение (σx )max существенно превосходит соответствующее значение напряжения σx = σm = pa / 2h , следующего из расчета по безмоментной

теории, что подчеркивает необходимость учета краевого эффекта при расчете тонкостенных оболочек.

Изгиб длинной 12.3. цилиндрической оболочки нагрузкой, равномерно распределенной по круго-

вому сечению

В силу симметрии задачи будем рассматривать половину цилиндра, расположенную справа от оси z . Отметим, что каждая половина цилиндра воспринимает половину внешней нагрузки, и поэтому при x = 0 имеем Q0 = −P / 2 .

Примем во внимание, что для больших значений переменной x (оболочка длинная) прогиб должен быть конечным ( C1 = C2 = 0 ). Кроме того, поскольку в

рассматриваемой задаче давление, распределенное по поверхности оболочки отсутствует, частное решение уравнения прогибов, определяемое этим давлением, имеет вид w1 = 0 . Соответственно, общее решение уравнения прогибов принима-

ет форму:

w = e−βx (C cosβx +C	4	sin βx) .
3	4

Для длинного цилиндра функция w должна быть симметрична относительно оси z . Данное требование определяет граничное условие для половины цилиндра: в сечении x = 0 производная dw/ dx должна быт равна нулю.

Таким образом, для отыскания постоянных ничные условия:

				d w		= 0
					dx	= 0
					dx	x=0
						x=0
Q	x		= Q		= − D		d 3w
							d 3w

		x=0	0				d x	3
		x=0	0					3

Выполняя граничные условия, получим:

C3 и C4 имеем следующие гра-

	= −	P	.

x=0	2

224

8β3D

C3 = C4	=	P	.
		8β3D

Окончательно, соотношение, определяющее прогиб оболочки при приложении нагрузки, равномерно распределенной по круговому сечению, имеет вид:

w = Pe−βx (cosβx +sin βx) .

Наибольший прогиб и наибольший изгибающий момент имеют место при x = 0 :

w	=	P	= Pa2 β ,	(M	x	)	=	P	.

max		8β3D	2Eh			max		4β

Легко установить, что всеми величинами, определяемыми в рассматриваемой задаче, можно пренебречь при x ≥ π/ β , что означает локальный характер действия приложенной нагрузки и соответствует общей оценке протяженности зоны краевого эффекта βL / 2 > π , где L − длина оболочки.

12.4.

Изгиб длинной цилиндрической оболочки нагрузкой, равномерно распределенной по краю

Общее решение уравнения прогибов имеет вид:

		w = e−βx (C3 cosβx +C4 sin βx) .
При заданном нагружении края оболочки						x = 0 постоянные интегрирования
C3 и C4 должны быть найдены из следующих граничных условий:
− D	d 2w		= M 0	,	− D	d 3w		= Q0 .

	dx	2				d x3
			x=0				x=0

225

Подставляя значения производных функции w в граничные условия и проводя соответствующие преобразования, получим:

C = −

Q0 + M

0β

= −

M 0

2β3D

2β2D

Подставим значения постоянных C3 и C4

в соотношение для прогиба w . Бу-

дем иметь:

w =

e−βx

[βM

sin βx −(

βM

+Q )cosβx] .

2β3D

Наибольший прогиб имеет место на загруженном торце при x = 0 :

= w = −

(

βM

+Q )

x=0

max

2β3D

где знак « − » показывает, что прогиб направлен в сторону, обратную направлению оси z . Угол поворота сечения (наклон) при x = 0 определится соотношением:

dw		=	1	(2βM	0	+Q	) .

dx	x=0		2β2D				0

12.5.

Изгиб короткой цилиндрической оболочки перерезывающими силами, равномерно распределенными по краю

Для длинных цилиндрических оболочек взаимным влиянием краев можно пренебречь, что позволяет строить решение на одном краю независимо от другого. В случае коротких оболочек взаимное влияние краев необходимо учитывать и применять общее решение дифференциального уравнения прогибов, содержащее четыре постоянные интегрирования:

w = eβx (C cosβx +C	2	sin βx)+e	−βx (C	cosβx +C	4	sin βx)+ w ,
1	2		3		4	1
		226

где w1 − частное решение уравнения прогибов, определяемое давлением p , распределенным по поверхности оболочки.

Примем во внимание, что в рассматриваемой задаче p = 0 , и перепишем функцию прогибов w в форме:

w =C1 sin βx sh βx +C2 sin βx ch βx +C3 cosβx sh βx +C4 cosβx ch βx .

Преимущество такой записи решения заключается в том, что если ввести систему координат так, как показано на рисунке, то сразу должны принять C2 = C3 = 0 , так как функция прогибов w должна быть четной относительно x .

Постоянные C1 и C4 должны быть найдены из граничных условий на торце оболочки (краю), которые в данной задаче имеют вид:

M x

= − D

d 2w

= 0

x=l / 2

d 3w

= − D

= −Q .

x=l / 2

d x

x=l / 2

Подставляя производные функции прогибов w в представленные граничные условия и решая полученную систему уравнений относительно постоянных C1 и

C4 , получим:

C	= −	Q0	sin αshα	, C	4	= −	Q0	cos αchα	,
1		β3D sin 2α +sh2α			4		β3D sin 2α +sh2α
		β3D sin 2α +sh2α					β3D sin 2α +sh2α

где α = βl / 2 .

Прогиб и наклон на конце цилиндра при x = l / 2 принимают следующие значения:

cos 2α +ch2α

2Q a

2β

(2α) ,

= −

x=l / 2

2β3D sin 2α +sh 2α

x=l / 2

E h

2Q a2β2 sh 2α −sin 2α

2Q a

2β2

(2α) ,

= −

χ2

E h

sin 2α +sh 2α

E h

x=l / 2

где χ1(2α), χ2 (2α) − тригонометрические функции, значения которых приведены в таблицах, имеющихся в литературе.

227

12.6.	Изгиб	короткой ци-
	Изгиб	короткой ци-
	линдрической оболочки
	изгибающими моментами,
	равномерно	распределен-
	ными по краю

Решение поставленной задачи строится по схеме, предложенной в задаче об изгибе короткой цилиндрической оболочки перерезывающими силами, равномерно распределенными по краю.

Функцию прогибов принимаем в виде:

w = C1 sin βxshβx +C4 cosβx chβx .

M x

= − D

d 2w

= M0 ,

x=l / 2

dx2

x=l / 2

= − D

d 3w

x=l / 2

= 0 .

d x

x=l / 2

Определяя значения постоянных C1

и C4 , будем иметь:

= − M 0

sin 2αch2α +sh 2αcos2 α ,

2β2D

(sin 2α +sh 2α)cos αchα

= −

M 0 cos αshα −sin αchα

β2D

sin 2α +sh2α

Прогиб и наклон на конце цилиндра при x = l / 2 принимают следующие значения:


w	x=l / 2 = −		2M 0 a2β2			χ2		(2α)	,
			2M 0 a2β2
				E h
				E h
dw				4M 0 a	2β3
dw				4M 0 a	2β3
dx		= −		E h			χ3 (2α)		,
		x= l / 2
		x= l / 2

228

где к ранее введенным тригонометрическим функциям χ1(2α), χ2 (2α) добавилась функция

χ3	(2α)= ch2α−cos2α	,
	sin 2α+sh2α

значения которой также имеются в таблицах.

Отметим, что при достаточно больших значениях параметра α (возрастание α определяет возрастание длины оболочки l ) функции χ1(2α), χ2 (2α), χ3(2α) близки к единице. Можно видеть, что в этом случае решения задач для коротких оболочек переходят в решения для длинных. Анализ показывает, что при 2α = 3,5 ÷4 цилиндрическую оболочку можно считать длинной.


12.7.	Длинная		цилин-
12.7.	дрическая		обо-
	дрическая		обо-
	лочка,	усиленная
	равноотстоящими
	кольцами,		нагру-
	женная	равномер-
	ным	внутренним
	давлением р

Приведенные выше решения задач об изгибе короткой цилиндрической оболочки нагрузками, равномерно распределенными по краю, могут быть использованы при рассмотрении ряда других задач, в частности, для решения поставленной.

Положим сначала, что колец нет; в этом случае радиус трубы увеличится на

величину δ = pa2 / Eh . При наличии колец между оболочкой и каждым кольцом возникают реактивные силы, величину которых на единицу длины окружности обозначим через P .

Для решения поставленной задачи можно принять расчетную схему, приведенную на рис. 12.9, где Q0 = −P / 2 .

Если принять, что подкрепляющие кольца являются абсолютно жесткими, сила P и момент M 0 должны быть определены из

условий, что под кольцом прогиб w равен δ

Рис. 12.9

и что наклон dw/ dx равен нулю. Записав эти два условия, будем иметь:

229

Pa2β

(2α)

2M 0 a2β2

χ2 (2α)=

pa2

x=l / 2 =

χ1

−

Pa2β2

χ2 (2α) −

4M 0 a

2β3

(2α)= 0 .

χ3

x= l / 2

E h

Решение полученных уравнений относительно силы P и момента M 0 дает:

P =

2 p

χ3

2χ χ

−χ2

M 0 =

χ2

2β2

2χ χ

−χ2

Теперь определение прогибов в поставленной задаче сведено к суммированию полученных ранее решений задач об изгибе короткой цилиндрической оболочки

нагрузками P и M 0 , с добавлением частного решения w1 = −pa2 / Eh , определяемого наличием внутреннего давления p .

При необходимости можно учесть деформирование (растяжение) подкрепляющих колец, учитывая, что сила P вызывает в кольце растягивающую силу

Pa , которая приводит к увеличению внутреннего радиуса δ1 = Pa2 / ES , где S −

площадь поперечного сечения кольца. Чтобы принять в расчет расширение подкрепляющего кольца, прогиб под кольцом теперь запишем в виде:

w x=l / 2 = δ−δ1 .

230

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 1819 / 2019 20 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.06.20151.24 Mб37rusadv.pdf
#
14.09.201977.82 Кб3rybka_sorted.doc
#
01.05.2025139.26 Кб0S1._Razdatohnyj_material.doc
#
27.03.20161.39 Mб18Sandrakova_Funktsii_mnogikh_peremennykh_2015.pdf
#
05.06.20151.44 Mб81Sapunov_Prikladnaya_teoriya_uprugosti_2008.pdf
#
05.06.20154.18 Mб248Sapunov_Prikladnaya_teoriya_uprugosti_ch1_2008.pdf
#
05.06.20153.03 Mб153Savelova_Metod_Monte-Karlo_2011.pdf
#
10.12.2018244.22 Кб1savova_ritorics.doc
#
01.04.202523.27 Mб0sbornik.docx
#
01.05.2025766.98 Кб0SCADA_full.doc
#
19.07.201923 Кб3Scientific American.docx