При отсутствии объемных сил имеем, что 2σ= 0 (σ – гармоническая функция). Применяя оператор Лапласа к каждому из уравнений Бельтрами – Митчелла, сразу же получаем, что

2 2σx = 0 и т.д.

Отметим, что приведение, например, уравнений Ламе к бигармоническим уравнениям и введение бигармонических функций Φ1 , Φ2 , Φ3 не говорит о том, что эти функции произвольные:

связь между ними определяется уравнениями Ламе.

5.6.Общее решение уравнений теории упругости

вперемещениях (метод П. Ф. Папковича)

Приведение однородных уравнений Ламе к бигармоническим уравнениям позволяет говорить о построении общего решения с использованием бигармонических функций, связанных между собой. Соответственно, возникает вопрос о возможности построения решения этих уравнений с использованием функций более простого типа и при этом независимых друг от друга.

Введем вспомогательную функцию θ = 2ψ. Так как 2θ = 0 , то ψ – бигармоническая функция. Подставим введенную функцию

θ = 2ψ в первое уравнение Ламе. Будем иметь:

Рассмотрев подобным образом оставшиеся два уравнения Ламе, можем утверждать, что функции

99

являются произвольными гармоническими функциями, так как они удовлетворяют уравнениям Ламе, но не связаны между собой. Учитывая, что 1+(λ/ μ)=1/(1−2ν), полученные соотношения можем

переписать в виде:

По найденным значениям u , v , w определим относительное изменение объема θ:

Учитывая, что функция ψ введена посредством соотношения

θ = 2ψ, получим следующее уравнение для определения этой бигармонической функции:

Простой подстановкой легко убедиться, что если мы возьмем ψ в виде

то уравнение удовлетворяется (здесь Φ0 – произвольная гармоническая функция). Зная теперь значение функции ψ , находим, что

100

Итак, общее решение однородных уравнений Ламе представлено через четыре произвольные, независимые друг от друга гармонические функции. Приведенная форма общего решения однородных уравнений Ламе принадлежит Папковичу П.Ф.

Анализ полученных соотношений показывает, что функция Φ0

может быть удалена из рассмотрения без ограничения общности решения.

Формулы Папковича П.Ф. дают общее решение уравнений Ламе, но решение задачи теории упругости на этом не исчерпывается – необходимо подчинить это решение конкретным граничным условиям.

В настоящее время общие решения используются чаще всего при решении трехмерных задач теории упругости.

5.7. Пропорциональность перемещений, напряжений и деформаций действующей нагрузке

Будем считать, что задача определения упругого равновесия при действии нагрузок X , Y , Z и X , Y , Z решена: получено решение уравнений Ламе u , v , w , удовлетворяющее заданным граничным условиям в напряжениях.

Примем, что значения действующих поверхностных и объемных

сил изменились пропорционально одному и тому же параметру

λ >1:

101

Посмотрим, как при этом изменятся перемещения, напряжения и деформации.

Сразу же видно, что в силу линейности и уравнений Ламе, и граничных условий, они будут удовлетворяться, если положить

u′ = λu , v′ = λv , w′ = λw ,

где u , v , w – перемещения, соответствующие «старой» внешней нагрузке. Следовательно, перемещения изменились пропорционально изменению внешней нагрузки.

Очевидно, что использование полученного результата в зависимостях Коши, а затем и в уравнениях линейного физического закона позволяет сделать вывод о пропорциональности и деформаций, и напряжений действующей внешней нагрузке.

Другим важным следствием линейности уравнений теории упругости является так называемый принцип независимости действия внешних сил (или принцип наложения).

Предположим, что нам известны перемещения точек u′, v′, w′ некоторого упругого тела, соответствующие приложенным внеш-

Принцип независимости действия сил утверждает, что в рамках

также являются решением уравнений Ламе и граничных условий.

С математической точки зрения построение доказательства базируется на возможности суммировать почленно уравнения Ламе и граничные условия в напряжениях, что позволительно в силу ли-

102

нейности рассматриваемых уравнений. С физической точки зрения, как уже отмечалось, эта процедура может привести к многозначности решения (например, задача Эйлера). В дальнейшем задачи, не отвечающие принципу независимости действия сил, рассматривать не будем.

Рассмотренные принципы в некоторых случаях позволяет свести решение сложной задачи линейной теории упругости к решению двух или нескольких более простых задач.

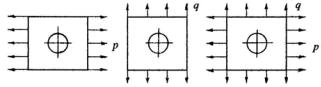
Пусть, например, известно решение задачи о растяжении квадратной пластины, имеющей круговое отверстие, силами p , равно-

мерно распределенными по двум её кромкам (рис. 5.1, а).

В силу пропорциональности перемещений напряжений и деформаций действующим внешним нагрузкам из этого решения сразу можно получить решение задачи о сжатии той же пластины силами q , равномерно распределенными по двум противоположным

кромкам (рис. 5.1, б). Для этого нужно ввести параметр λ = −q / p .

Далее, воспользовавшись принципом наложения, можно построить решение задачи о напряжениях в квадратной пластине, подвергающейся одновременно и растяжению, и сжатию (рис. 5.1, в).

Пользуясь принципом независимости действия сил, неоднородную задачу теории упругости (задачу с объемными силами, отличными от нуля) можно свести к однородной (с объемными силами, равными нулю). Действительно, решение неоднородной системы уравнений Ламе можем записать в виде:

103