
- •Содержание
- •1. Введение
- •1.3. Три закона деформирования сплошного твёрдого тела
- •2. Закон равновесия. Теория напряжений
- •2.1. Напряженное состояние в точке
- •2.2. Дифференциальные уравнения равновесия элемента сплошного твердого тела
- •2.3. Граничные условия в напряжениях
- •2.4. Анализ напряженного состояния в точке
- •2.4.2. Исследование нормальных напряжений
- •2.4.3. Исследование касательных напряжений
- •2.4.4. Поверхности напряжений
- •2.4.5. Графическое исследование напряжений. Круги Мора
- •3. Закон сплошности. Теория деформаций
- •3.2. Исследование деформированного состояния в точке
- •4. Физический закон. Обобщенный закон Гука
- •4.3. Основные упругие постоянные
- •5. Уравнения и задачи упругого равновесия
- •5.1. Основные граничные задачи теории упругости
- •5.2. Уравнения теории упругости в перемещениях
- •5.3. Уравнения теории упругости в напряжениях
- •5.6. Общее решение уравнений теории упругости
- •5.7. Пропорциональность перемещений, напряжений и деформаций действующей нагрузке
- •6. Постановка температурных задач линейной теории упругости
- •7. Постановка динамических задач линейной теории упругости
- •8. Криволинейные координаты
- •8.1. Уравнения линейной теории упругости
- •- граничные условия в напряжениях
- •8.2. Уравнения линейной теории упругости в сферических координатах
- •Из граничных условий в напряжениях на боковой поверхности вала остается только одно уравнение:
- •Под плоской задачей теории упругости понимают совокупность двух родственных в математическом отношении задач:
- •Список литературы
ε |
x |
= |
|
λ + μ |
|
σ |
x |
− |
|
|
λ |
|
|
(σ |
y |
+ σ |
z |
) , |
|||||
μ(3λ + 2μ) |
2μ(3λ + 2μ) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
ε |
y |
= |
|
λ + μ |
|
σ |
y |
− |
|
|
λ |
|
|
(σ |
z |
+ σ |
x |
) |
, |
||||
μ(3λ + 2μ) |
2μ(3λ + 2μ) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
ε |
z |
= |
|
λ + μ |
|
σ |
z |
− |
|
|
|
λ |
|
|
(σ |
x |
+ σ |
y |
) , |
||||
μ(3λ + 2μ) |
|
2μ(3λ + 2μ) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
γxy |
= |
1 |
τxy , |
γ yz = |
1 |
τyz , |
γzx = |
1 |
τzx . |
|
||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
μ |
|
|
|
|
|
μ |
|
|
|
|
μ |
|
|
|
|||||
Легко видеть, что для однозначного определения деформаций необходимо выполнение следующих условий: 3λ + 2μ ≠ 0 и μ ≠ 0 .
4.3. Основные упругие постоянные
Упругие свойства однородного изотропного тела (модели тела в теории упругости) характеризуются двумя упругими постоянными Ламе λ и μ. Чтобы иметь возможность определять эти постоянные
из экспериментов, очевидно, необходимо выяснить физический смысл этих постоянных, а если это не удается сделать, то физический смысл любых комбинаций этих постоянных. Желательно, конечно, чтобы эти упругие постоянные (или их комбинации) определялись из простейших экспериментов.
Рассмотрим частный случай напряженного состояния, когда компоненты напряжений имеют следующие значения:
σx =T = const , σx = σy = σz = τxy = τyz = τzx = 0 .
Соответствующие им компоненты деформаций имеют вид:
|
λ + μ |
|
|
λ |
|
||
εx = |
|
T |
, |
εy = εz = − |
|
T |
, |
μ(3λ + 2μ) |
2μ(3λ + 2μ) |
||||||
γxy = γyz = γzx = 0 .
79

Предположим, что упругое тело, в котором реализовано данное напряженное состояние, есть тело цилиндрической (или призматической) формы с образующими, параллельными оси x , и основаниями, перпендикулярными к ней.
Используя граничные условия в напряжениях, по заданным компонентам напряжений восстановим внешние нагрузки, действующие на тело. Сразу можем записать, что на боковой поверхности поверхностные силы равны нулю, т.е. боковая поверхность свободна от нагрузок. Действительно, в общем случае
X = σxl + τxy m + τxz n ,
Y = τyxl + σy m + τyz n ,
Z = . . . ,
но для боковой поверхности l = 0 , m ≠ 0 , n ≠ 0 и X =Y = Z = 0 . На основании, обращенном в сторону положительной оси x , будем иметь: X = Т , Y = Z = 0 ( l =1, m = 0 , n = 0 ), а на другом
основании: X = − Т , Y = Z = 0 ( l = −1 , m = 0 , n = 0 ).
Очевидно, что если Т > 0, то имеем задачу растяжения рассматриваемого тела в направлении оси x . При этом происходит удлинение цилиндра в продольном направлении и сжатие в поперечном. Это значит, что при Т > 0 мы должны записать:
εx > 0 , εy = εz < 0 .
Данное утверждение можно считать доказанным экспериментально. Также из эксперимента можно выявить наличие двух упругих постоянных материала:
E = |
T |
|
εy |
|
|
|
εz |
|
|
|
и ν = |
|
|
= |
|
|
. |
||||
|
|
|
|
|
|
|||||
|
εx |
|
εx |
|
|
|
εx |
|
||
80
Величина E носит название модуля упругости или модуля Юнга и определяется как отношение растягивающего напряжения к вызываемому им относительному продольному удлиненно (или сжимающего напряжения к продольному относительному сжатию) при одноосном растяжении (сжатии).
Физическое значение величины ν (коэффициента Пуассона) следует из приведенных соотношений: отношение относительного поперечного сжатия к относительному продольному удлинению при растяжении (или отношение поперечного расширения к продольному сжатию при сжатии) есть величина постоянная, не зависящая от формы сечения растягиваемого стержня и от величины растягиваемого усилия.
Сопоставление соотношений, полученных экспериментально, и записанных ранее формул для εx , εy , εz , определяющих дефор-
мирование модели упругого тела при растяжении, позволяет получить:
μ (3λ + 2μ) |
= E , |
λ |
|
|
|
= ν . |
|
λ + μ |
2 (λ + μ) |
||
Полученные соотношения дают возможность выразить «старые упругие постоянные» λ и μ через «новые» E и ν :
λ = |
|
E ν |
, |
|
(1 + ν)(1 − 2ν) |
||||
|
|
E |
|
|
μ = |
|
. |
|
|
2 (1 + ν) |
|
|||
Аналогично модулю упругости E при растяжении вводят понятие модуля упругости при сдвиге (кручении) или модуля упругости второго рода как отношение касательного напряжения к соответствующей деформации сдвига, и вводят для него обозначение G . Из
формул для угловых деформаций (деформаций сдвига) видим, что
G = μ .
81
Запишем уравнения физического закона, пользуясь новыми упругими характеристиками E и ν . Они будут иметь следующий вид:
εx = |
1 |
|
[σx − ν (σy + σz )] |
, |
γxy = |
2 (1 + ν) |
τxy , |
|||
E |
|
E |
|
|||||||
|
|
|
|
|
|
|
||||
εy = |
1 |
|
[σy − ν (σz + σx )] |
, |
γ yz = |
2 (1 + ν) |
|
τyz , |
||
E |
|
E |
||||||||
|
|
|
|
|
|
|
||||
εz = |
|
1 |
|
[σz −ν (σx +σy )] |
, |
γzx = |
|
2 (1 + ν) |
τzx , |
|
|
E |
|
E |
|||||||
|
|
|
|
|
|
|
||||
Выписанные соотношения часто называют обобщенным законом Гука.
Складывая первые три уравнения физического закона, получим следующую зависимость между относительным изменением объема и суммой нормальных напряжений:
θ = (1− 2ν)(σx + σy + σz )/ E .
В случае равномерного гидростатического давления (сжатия) p имеем σx = σy = σz = −p и тогда
θ = − |
3(1 − 2ν) |
p . |
||
E |
|
|||
|
|
|||
Полученная формула устанавливает связь между относительным изменением объема (объемной деформации) и гидростатическим давлением. Величину K = E / 3(1− 2ν) называют модулем
объемной деформации (модулем всестороннего сжатия). Очевидно, что при p > 0 происходит уменьшение объема, т.е. K > 0 . Отсюда
сразу следует, что для упругого тела коэффициент Пуассона всегда меньше 1/2 ( ν <1/ 2 ).
82
Модуль объемной деформации, представленный через постоянные Ламе, имеет вид
|
K = λ + |
2 |
μ . |
|
|
3 |
|
||||
|
|
|
|
|
|
|
Задачи |
|
|||
|
|
|
|
|
|
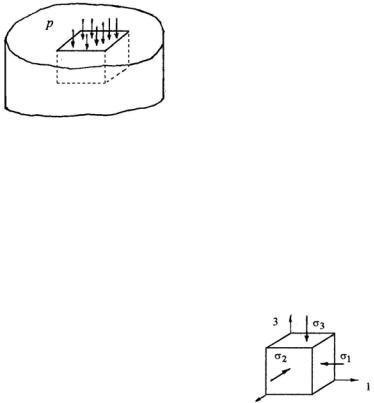
4.1. |
|
|
|
Стальной кубик, |
вставленный |
|
|
плотно без зазоров |
в отверстие |
||
|
|
|
|||
|
|
|
(паз) в массивной плите, вдавли- |
||
|
|
|
вается в нее давлением p . При- |
||
|
|
|
нимая плиту абсолютно жесткой |
||
|
|
|
и полагая, что трение между гра- |
||
|
|
|
нями кубика и стенками паза от- |
||
|
|
|
сутствует, найти давление на |
||
|
|
|
стенки паза. |
|
|
|
|
|
|
|
|
Из физических соображений ясно, что если кубик считать недеформируемым (абсолютно жестким), то давление на стенки паза будет равно нулю. С другой стороны, давление на стенки паза было бы равно p , если бы материал кубика вел
бы себя как несжимаемая жидкость. Очевидно, что эти две оценки являются крайними.
Для решения поставленной задачи необходимо привлечь уравнения физического закона, поскольку в решении должны фигурировать характеристики материала кубика.
Рассмотрим напряженное и деформированное состояние элемента, выделенного в кубике (рис. 4.3).
Можно утверждать, что грани элемента являются главными площадками, так как на них касательные напряжения равны нулю (трение между гранями кубика и стенками паза отсутствует). Поскольку давление на стенки паза по модулю должно быть меньше p , имеем σ3 = − p . С другой стороны, принимая
плиту абсолютно жесткой, получаем ε1 = ε2 = 0 . Рис. 4.3
Оставшиеся неизвестные параметры напряженного и деформированного состояния элемента σ1 = σ2 и ε3 определим из уравнений физического закона:
83
ε = |
1 |
[σ −ν(σ |
2 |
|
+σ |
3 |
)] |
, |
||||||||||||||||
|
|
|
||||||||||||||||||||||
|
1 |
|
E |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ε |
2 |
= |
1 |
|
[σ |
2 |
−ν(σ |
3 |
+σ )] |
, |
||||||||||||||
|
|
|||||||||||||||||||||||
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ε |
3 |
= |
|
1 |
[σ |
3 |
−ν(σ +σ |
2 |
)] . |
|||||||||||||||
|
|
|||||||||||||||||||||||
|
|
|
|
E |
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для определения напряжений σ1 = σ2 |
достаточно рассмотреть первое уравнение, |
|||||||||||||||||||||||
откуда получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
|
|
= σ |
2 |
= |
|
|
ν |
|
|
|
σ |
3 |
|
|
|
. |
|
|||
|
|
|
|
|
1 |
−ν |
|
|
|
|
||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Анализ данного соотношения позволяет получить интервал изменения коэффициента Пуассона: 0 < ν ≥1/ 2 .
4.2. |
Показать, что деформированное состояние εx = −εy = Asin 2α , |
|
γxy = Acos 2α, εz = γyz = γzx = 0 , где A − постоянная, эквива- |
|
лентно простому сдвигу от τ. |
|
|
Будем считать, в системе координат xoy реализовано состояние простого
(чистого) сдвига. Соответствующее деформированное состояние имеет вид:
εx = εy = 0 , γxy = γ = τ/ μ .
Перейдем к новой системе координат xoy , повернутой относительно старой на угол α . Учитывая значения направляющих косинусов ( l1 = cosα , m1 = sin α
для оси x ; l 2 = −sin α , m 2 = cosα для оси y ), деформированное состояние в новой системе координат будет определяться следующими соотношениями:
|
|
|
ε |
x |
= ε |
x |
l 2 |
+ε |
y |
m2 |
+ γ |
xy |
l m |
|
|
|
ε |
x |
= |
τ |
sin 2α |
|
, |
|||||||||||||
|
|
|
|
|
2μ |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
εy = εx l 22 +εy m22 + γxy l 2m 2 |
|
|
|
εy = − |
|
τ |
sin 2α |
, |
|||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
2μ |
|||||||||||||||||||||||||||||||
γ |
xy |
= ε |
x |
l |
1 |
l |
2 |
+ε |
y |
m |
1 |
m |
2 |
+ |
γxy |
(l m |
+l |
2 |
m |
1 |
) |
|
γ |
xy |
= |
τ |
cos 2α . |
|||||||||
2 |
|
2μ |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Полученное деформированное состояние эквивалентно простому сдвигу от τ и соответствует деформированному состоянию, заданному в условии задачи, при
A = τ/ 2μ .
84
