ляется углом поворота диагонали. При повороте грани как единого целого происходит поворот одновременно двух отрезков AB и AD (рис. 3.2, а).

Пусть у нас повернется только один отрезок AB (рис. 3.2, б), но при построении повернутого элемента учтем, что εx = εy = 0 (нет

линейных деформаций). Из рис. 3.2, б непосредственно видно, чтоCAC′ = (1/2) CDC′ (угол CAC′ вписанный, а CDC′ – центральный). Но угол CDC′ сам положительный (производная ∂u / ∂y > 0 ), а поворот отрезка отрицательный (принимаем, что положительное вращение − против часовой стрелки). Итак, CAC′ = – (1/2) ∂u / ∂y .

Соответственно, рассмотрев поворот отрезка AD (рис. 3.2, в) получаем, что диагональ повернется на угол величиной (1/2) ∂v / ∂x (здесь поворот отрицательный, как и для предыдущего случая, но и сам угол отрицательный, поскольку приращение ∂v отрицательное

Рассматривая повороты граней в остальных двух координатных плоскостях, получим аналогичные соотношения:

3.2. Исследование деформированного состояния в точке

Описание деформирования элемента тела в форме прямоугольного параллелепипеда привело к введению шести характеристик

52

деформирования (компонентов деформаций): εx , εy , εz , γxy , γyz , γzx , из которых первые три определяют линейную деформацию

отрезков, параллельных координатным осям, а вторые три − изменение прямых углов, образованных такими отрезками и расположенных в координатных плоскостях.

Деформированное состояние в точке определяется совокупностью деформаций всех линейных элементов, проходящих через данную точку (здесь имеются в виду и линейные деформации, и деформации сдвига).

Можно показать, что линейная деформация произвольно ориентированного отрезка представляется шестью компонентами деформации прямоугольного параллелепипеда.

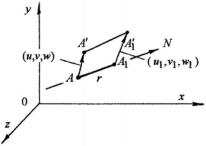
На произвольном направлении N возьмем отрезок AA1

малой длины r (рис. 3.3). Линейная деформация εN отрезка

AA1 определяется соотношением:

Пусть компоненты вектора перемещения точки A будут u , v и w . Тогда компоненты перемещения точки A1 можно представить соотношениями:

53

Проекции отрезка r на оси x , y , z равны dx , dy , dz . После деформации длина отрезка становится равной r1 . Соответственно, проекции отрезка r1 на оси будут определяться соотношениями:

dx + (u1 −u) , dy +(v1 −v) , dz + (w1 − w) .

Определяя длину отрезка r1 по его проекциям на координатные оси, получим:

С другой стороны, длину отрезка r1 можем найти из соотношения, определяющего линейную деформацию εN . Будем иметь:

r1 = r (1+ εN ) .

Из сопоставления полученных соотношений следует уравнение, связывающее деформацию εN с приращениями перемещений:

r2 (1+ 2εN +ε2N )= (dx + du)2 +(dy + d v)2 +(d z + dw)2 .

Подставим сюда значения du , dv , dw и учтем, что деформации

и производные от перемещений u , v , w малы (их квадратами и произведениями можно пренебречь по сравнению с первыми степенями). Будем иметь:

54

Полученное уравнение можно преобразовать, учитывая, что r2 = dx2 + d y2 + dz2 . Кроме того, поскольку направление N задано направляющими косинусами l , m , n , то в этом случае

dx / r = l , dy / r = m и т.д.

Группируя соответствующим образом производные от перемещений и заменяя их на деформации в соответствии с зависимостями Коши, после всех преобразований получим

εN = εxl2 +εym2 +εzn2 + γxyl m + γyzm n + γzxn l .

Таким образом, линейная деформация в данной точке по любому направлению N представляется через шесть компонентов деформации прямоугольного параллелепипеда.

С помощью полученной формулы можно легко получить формулы преобразований линейных деформаций при переходе к новым координатным осям. Если мы введем новую координатную

εy′ = . . . ,

εz′ = . . .

Сравним формулы преобразований для линейных деформаций с формулами преобразований для нормальных напряжений. Видим, что запись окажется аналогичной, если оперировать половинками деформаций сдвига, т.е. величинами

γxy / 2 , γyz / 2 , γzx / 2 .

Учитывая, что формулы преобразований линейных деформаций при переходе к новым координатным осям аналогичны соответст-

55

вующим формулам преобразований компонентов тензора напряжений, можем говорить о тензоре деформаций с учетом сделанного выше замечания относительно половинок деформаций сдвига:

Так же, как и тензор напряжений, тензор деформаций является тензором второго ранга, симметричным относительно главной диагонали.

Дальнейшее исследование компонентов тензора деформаций (деформированного состояния) можно вести по той же схеме, что и для компонентов тензора напряжений. Очевидно, что результаты исследования будут аналогичны результатам, полученным ранее при исследовании напряжений (компоненты тензоров должны обладать одинаковыми свойствами). При исследовании получим:

- имеются три главные взаимно перпендикулярные оси линейных деформаций и соответственно им три главные линейные деформации ε1 , ε2 , ε3 ;

-на плоскостях, определяемых главными осями линейных деформаций, деформации сдвига равны нулю;

-имеются три главных сдвига γ1 , γ2 , γ3 , которые равны разно-

стям главных линейных деформаций γ1 = ε2 − ε3 , γ2 = ε3 − ε1 ,

γ3 = ε1 − ε2 ;

-имеются три инварианта тензора деформаций:

I1ε = εx + εy + εz = ε1 + ε2 + ε3 ,

56

Линейный инвариант I1ε представляет собой относительное из-

менение объема. Это легко проверить, рассмотрев элемент, ребра которого до деформации равны dx , dy , dz . После деформации

они будут равны соответственно (1+ε1)dx , (1+ ε2 )d y , (1+ ε3 )dz . Следовательно,

V + V = (1+ ε1)(1 + ε2 )(1+ ε3 )dxd ydz = (1+ ε1 + ε2 + ε3 )dxd ydz .

Относительное изменение объема V /V = ε1 + ε2 + ε3 . Для величины относительного изменения объема вводят обозначение θ;

- возможно построение кругов Мора для деформированного состояния в точке. Точки области, ограниченной тремя кругами Мора, будут определять деформации всех линейных элементов, проходящих через данную точку.

3.3.Определение перемещений по заданным деформациям. Уравнения совместности деформаций Сен-Венана

Зависимости Коши дают возможность вычислять компоненты деформаций εx , εy , . . . по заданным перемещениям u , v , w .

Поставим обратную задачу: вычислить компоненты перемещений u , v , w , если заданы компоненты деформаций как функции координат x , y , z .

Рассматривая зависимости Коши, легко убедиться, что произвольное задание компонентов деформаций не дает возможности однозначного определения компонентов перемещений, поскольку имеем шесть уравнений для отыскания трех искомых функций. Необходимо, чтобы деформации удовлетворяли еще каким-то вполне определенным соотношениям (были связаны каким-то образом между собой) для того, чтобы задача имела единственное решение.

Этот вывод следует также и из следующего геометрического рассмотрения. Представим себе тело разбитым на бесконечно малые элементы, например кубики (не считая элементов, примкнув-

57

ших к границе). Если мы подвергнем наши кубики заданным произвольным деформациям и затем попытаемся их сложить так, чтобы грани, соприкасавшиеся до деформации, снова соприкасались, то это окажется невозможным. Это еще раз показывает, что компоненты деформаций должны удовлетворять некоторым соотношениям для того, чтобы была возможность деформирования тела без разрывов.

Данное утверждение докажем, решая поставленную задачу об отыскании компонентов перемещений по заданным компонентам деформаций.

Пусть V – односвязная область изменения переменных x , y , z ,

вкоторой заданы деформации и в которой ищутся перемещения u ,

v, w . Будем считать, что имеем точку области M0 (x0 , y0 , z0 ), для

которой известны (заданы) компоненты перемещения u0 , v0 , w0 и компоненты вращения ωx0 , ωy0 , ωz0 . Точка M1 (x1 , y1 , z1) – произвольная точка области. Наша задача – найти компоненты перемещения u1 , v1 , w1 этой точки.

Пусть M0M1 определяет какую-либо линию, соединяющую точки M0 и M1 в области V . Поскольку точки M0 и M1 распо-

ложены на произвольном расстоянии друг от друга, для определения перемещения u1 нужно брать интеграл, чтобы определить пол-

ное приращение функции u на пути интегрирования M0M1 :

Для решения поставленной задачи значения частных производных ∂u / ∂x , ∂u / ∂y , ∂u / ∂z нужно представить через заданные

компоненты деформаций, однако сразу это можно сделать только для производной ∂u / ∂x :

∂u / ∂x = εx .

58

Для двух других производных можем записать:

Отметим, что последние два соотношения не решают полностью проблему представления частных производных ∂u / ∂y и ∂u / ∂z

через заданные компоненты деформаций, однако позволяют разбить интеграл на два. Будем иметь:

Первый интеграл уже состоит из заданных функций. Второй интеграл можем переписать в виде:

J2 = ∫(−ωzdy +ωyd z) = ∫(ωzd ( y1 − y) −ωyd (z1 − z)) .

M0M1 M 0M1

Разбиваем интеграл на два и берем каждый из них по частям. В частности, для первого будем иметь:

= −ωz0 (y1 − y0 ) − ∫(y1 − y)dωz .

M 0M1

С учетом полученного результата для второго интеграла получаем:

J2 = ∫(−ωzdy + ωyd z) = ωy0 (z1 − z0 ) −ωz0 (y1 − y0 )−

M 0M1

− ∫(y1 − y)dωz −(z1 − z)dωy .

M 0M1

59

Можно видеть, что для вычисления интеграла J2 необходимо знать значения приращений dωz и dωy , для отыскания которых необходимо представить производные функций ωz и ωy через

известные (заданные) компоненты деформации (или их производные). Оказывается, данная операция возможна. Например,

С учетом найденных значений производных соотношение для приращения dωz принимает вид:

и является известной функцией.

Значения производных функций ωx и ωy легко получить из выписанных соотношений круговой заменой индексов x , y , z .

Итак, для определения перемещения u1 в точке M1 окончательно имеем:

60

u1 = u0 + ωy0 (z1 − z0 ) −ωz0 (y1 − y0 )+

− ∫(y1 − y)dωz −(z1 − z)dωy ,

M 0M1

где dωz и dωy − уже известные функции. Объединим теперь оба интеграла в один, собирая слагаемые при dx , dy , dz :

u1 = u0 + ωy0 (z1 − z0 ) −ωz0 (y1 − y0 ) + ∫U xdx +U ydy +U zd z .

M 0M1

Здесь введены обозначения:

Совершенно аналогично можно записать соотношения, определяющие компоненты перемещений v1 и w1 в точке M1 . Будем

иметь:

v1 = v0 + ωz0 (x1 − x0 ) −ωx0 (z1 − z0 ) + ∫Vxdx +Vydy +Vzd z ,

M 0M1

w1 = w0 + ωx0 (y1 − y0 ) −ωy0 (x1 − x0 ) + ∫Wxdx +Wydy +Wzd z .

M 0M1

Полученные формулы определяют перемещения u1 , v1 и w1 в любой произвольной точке M1 тела, если заданы компоненты пе-

61

ремещения и компоненты вращения в точке M0 и компоненты де-

формации во всей области, занятой телом. Однако нами до сих пор не решен вопрос об однозначности определения этих перемещений, который мы затронули в начале раздела.

Рассматривая полученные соотношения, легко видеть, что требование однозначности определения перемещений u1 , v1 , w1 , по

существу, сводится к требованию независимости криволинейных интегралов, имеющих место в формулах, от пути интегрирования.

Из теории криволинейных интегралов известно, что для того, чтобы криволинейный интеграл не зависел от пути интегрирования, необходимо выполнить определенные требования. В нашем случае, например, для интеграла

∫ U xdx +U ydy +U zd z

M 0M1

эти требования имеют вид:

Подставляя в первое условие значения функций U x и U y , после некоторых простых преобразований приведем его к виду:

Полученное равенство должно быть справедливо при любых значениях координат y1 и z1 , и поэтому оно разбивается на два

условия и приводится к следующим двум уравнениям, связываю-

62

щим деформации:

Из остальных требований независимости интегралов от пути интегрирования следуют еще четыре (по два уравнения каждого типа) аналогичных независимых уравнения, однако их можно записать, используя круговую замену переменных x , y , z :

Полученные соотношения носят название условий совместности (условий неразрывности) деформаций Сен-Венана. Именно этим соотношениям должны удовлетворять заданные компоненты деформации, чтобы по ним можно было бы однозначно определить перемещения.

При соблюдении условий совместности деформаций формулы для перемещений u1 , v1 , w1 дают вполне определенные значения,

не зависящие от пути интегрирования. При этом постоянные величины u0 , v0 , w0 , ωx0 , ωy0 , ωz0 остаются произвольными, и, из-

63

меняя эти постоянные, можем сообщить телу только «жесткое» перемещение как целого. Действительно, если мы к каким-либо найденным перемещениям u , v , w добавим, соответственно,

u = u0 +ωy0z −ωz0 y ,

v = v0 +ωz0 x −ωx0z , w = w0 + ωx0 y −ωy0x ,

то эти добавки никаких дополнительных деформаций не вызовут.

решения поставленной задачи.

Задачи

3.1. Провести преобразования некоторых компонентов деформированного состояния, например, εz и γxy , при повороте системы

прямоугольных координат xyz вокруг оси y на 180°.

Указание. Использовать формулы, аналогичные формулам преобразования компонентов напряженного состояния при переходе от одной системы прямоугольных координат к другой, с учетом отличия тензора деформаций от тензора напряжений.

3.2. Деформированное состояние в точке задано следующими составляющими:

εz = γyz = γzx = 0 ,

где ϕ = ϕ(x, y). Выяснить, можно ли функцию ϕ считать произвольной функцией координат x, y ?

Известно, что для однозначного определения поля перемещений по заданному полю деформаций необходимо, чтобы деформации отвечали условиям (уравнени-

64