
- •Типовой расчёт Производная и дифференциал функции двух переменных. Исследование функции двух переменных.
- •Образец решения типового расчёта.
- •Вариант № 2.
- •Вариант № 3.
- •Вариант № 4.
- •Вариант № 5.
- •Вариант № 6.
- •Вариант № 7.
- •Вариант № 8.
- •Вариант № 9.
- •Вариант № 10.
- •Вариант № 11.
- •Вариант № 12.
- •Вариант № 13.
- •Вариант № 14.
- •Вариант № 15.
Типовой расчёт Производная и дифференциал функции двух переменных. Исследование функции двух переменных.
Образец решения типового расчёта.
Задание
1. Найти и изобразить на плоскости область
определения функции двух переменных:
 .
.
Решение.
Очевидно, аналитическое выражение,
задающее данную функцию, имеет смысл
тогда и только тогда, когда знаменатель
дроби не равен нулю:
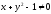 .
Уравнение
.
Уравнение
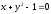 задаёт на координатной плоскости
задаёт на координатной плоскости
 параболу
параболу
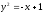 ,
вершина которой находится в точке
,
вершина которой находится в точке
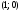 ,
ветви направлены влево, а осью симметрии
является ось абсцисс. Таким образом,
областью определения данной функции
являются все точки координатной
плоскости, кроме тех, что лежат на
параболе
,
ветви направлены влево, а осью симметрии
является ось абсцисс. Таким образом,
областью определения данной функции
являются все точки координатной
плоскости, кроме тех, что лежат на
параболе
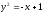 .
.
Задание 2. Найти частные производные первого порядка функций двух переменных:
2.1.
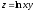 .
.
Решение.
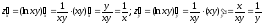 .
.
2.2.
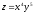 .
.
Решение.
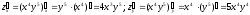 .
.
2.3.
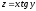 .
.
Решение.
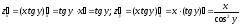 .
.
Задание
3. Найти все частные производные второго
порядка функции двух переменных:
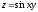 .
.
Решение. Сначала найдём частные производные первого порядка:
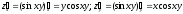 .
.
Теперь
находим производные второго порядка
по переменным
 и
и
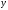 :
:
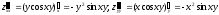 .
.
Находим смешанные производные:
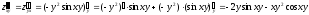 .
.
Задание
4. Найти производную функции
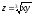 в точке
в точке
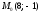 по направлению вектора
по направлению вектора
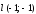 .
.
Решение.
Производная функции
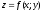 по направлению вектора
по направлению вектора
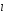 равна:
равна:
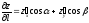 ,
где
,
где
 направляющие косинусы вектора
направляющие косинусы вектора
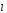 .
.
Находим частные производные данной функции:
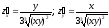 .
.
Находим
значения частных производных в точке
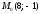 :
:
 .
.
Находим
направляющие косинусы вектора
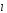 :
:
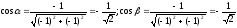 .
.
Окончательно получим:
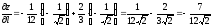 .
.
Задание
5. Найти градиент функции
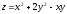 в точке
в точке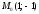 .
.
Решение.
Градиент функции двух переменных
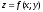 равен
равен
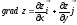 .
.
Найдём частные производные:
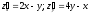 .
.
Найдём
значения частных производных в точке
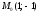 :
:
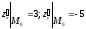 .
.
Тогда
градиент равен
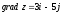 .
.
Задание
6. Исследовать функцию
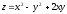 на экстремумы.
на экстремумы.
Решение.
Областью определения данной функции
является вся числовая плоскость
 .
Найдём частные производные данной
функции:
.
Найдём частные производные данной
функции:
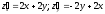 .
.
Производные первого порядка непрерывны на всей области определения функции. Для того, чтобы найти критические (стационарные) точки функции, решим систему уравнений:
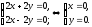
Получили
одну стационарную критическую точку
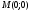 .
Для того, чтобы выяснить, является ли
она точкой экстремума, найдём производные
второго порядка.
.
Для того, чтобы выяснить, является ли
она точкой экстремума, найдём производные
второго порядка.
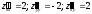 .
.
Найдём
дискриминант:
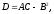 где
где
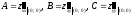 .
.
В
данном случае,
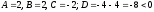 .
В данной точке экстремума нет.
.
В данной точке экстремума нет.
Задание
7. Найти экстремум функции
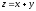 при условии
при условии
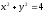 .
.
Решение.
Областью определения данной функции
является вся числовая плоскость
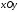 .
Выразим из уравнения связи
.
Выразим из уравнения связи
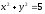 переменную
переменную
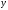 :
:
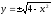 .
Далее рассмотрим оба возможных случая.
.
Далее рассмотрим оба возможных случая.
1)
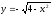 .
Подставляя это выражение в исходную
функцию, получим функцию одной переменной
.
Подставляя это выражение в исходную
функцию, получим функцию одной переменной
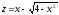 .
Исследуем эту функцию на наибольшее и
наименьшее значение при
.
Исследуем эту функцию на наибольшее и
наименьшее значение при
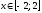 .
.
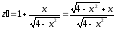 .
Очевидно,
.
Очевидно,
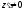 при любых значениях переменной
при любых значениях переменной
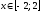 ,
и поэтому наибольшее и наименьшее
значение достигается в концах отрезка.
,
и поэтому наибольшее и наименьшее
значение достигается в концах отрезка.
 .
.
2)
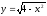 .
Подставляя это выражение в исходную
функцию, получим функцию одной переменной
.
Подставляя это выражение в исходную
функцию, получим функцию одной переменной
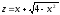 .
Исследуем эту функцию на наибольшее и
наименьшее значение при
.
Исследуем эту функцию на наибольшее и
наименьшее значение при
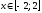 .
.
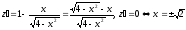 .
Получили две стационарные критические
точки. Найдём значения функции в этих
точках и на концах отрезка.
.
Получили две стационарные критические
точки. Найдём значения функции в этих
точках и на концах отрезка.
 .
.
Таким
образом,
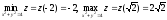 .
.
Задание
8. Найти наибольшее и наименьшее значение
функции
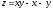 в области
в области
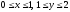 .
.
Решение. Прежде
всего, заметим, что данная функция
непрерывна в рассматриваемой области.
Найдём критические (стационарные) точки
функции, принадлежащие указанной
области. Частные производные первого
порядка
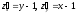 непрерывны в данной области. Составим
систему уравнений:
непрерывны в данной области. Составим
систему уравнений:
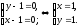
Получили
одну стационарную критическую точку
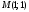 .
Найдём значение функции в этой точке:
.
Найдём значение функции в этой точке:
 .
Далее, последовательно найдём значения
функции на всех границах области.
.
Далее, последовательно найдём значения
функции на всех границах области.
1)
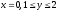 .
Функция принимает вид
.
Функция принимает вид
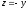 .
Тогда
.
Тогда
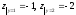 .
.
2)
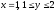 .
Функция принимает вид
.
Функция принимает вид
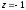 .
Тогда
.
Тогда
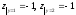 .
.
3)
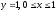 .
Функция принимает вид
.
Функция принимает вид
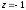 .
Тогда
.
Тогда
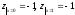 .
.
4)
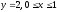 .
Функция принимает вид
.
Функция принимает вид
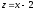 .
Тогда
.
Тогда
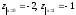 .
.
Получили:
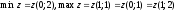
Задание
9. Найти с помощью полного дифференциала
приближённое значение выражения
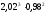
Решение.
Воспользуемся приближённым равенством
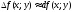 .
.
Отсюда
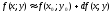 .
.
Рассмотрим
функцию
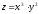 .
Найдём полный дифференциал этой функции:
.
Найдём полный дифференциал этой функции:
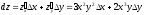 .
.
Примем
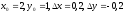 .
Тогда получим:
.
Тогда получим:
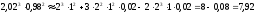 .
(Вычисление с помощью микрокалькулятора
даёт результат 7,916).
.
(Вычисление с помощью микрокалькулятора
даёт результат 7,916).
Вариант № 1.
Задание
1. Найти и изобразить на плоскости область
определения функции двух переменных:
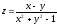 .
.
Задание 2. Найти частные производные первого порядка функций двух переменных:
2.1.
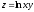 ;
2.2.
;
2.2.
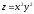 ;
2.3.
;
2.3.
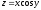 .
.
Задание
3. Найти все частные производные второго
порядка функции двух переменных:
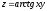 .
.
Задание
4. Найти производную функции
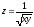 в точке
в точке
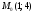 по направлению вектора
по направлению вектора
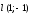 .
.
Задание
5. Найти градиент функции
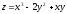 в точке
в точке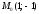 .
.
Задание
6. Исследовать функцию
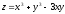 на экстремумы.
на экстремумы.
Задание
7. Найти экстремум функции
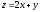 при условии
при условии
 .
.
Задание
8. Найти наибольшее и наименьшее значение
функции
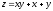 в области
в области
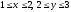 .
.
Задание
9. Найти с помощью полного дифференциала
приближённое значение выражения
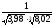 .
.
